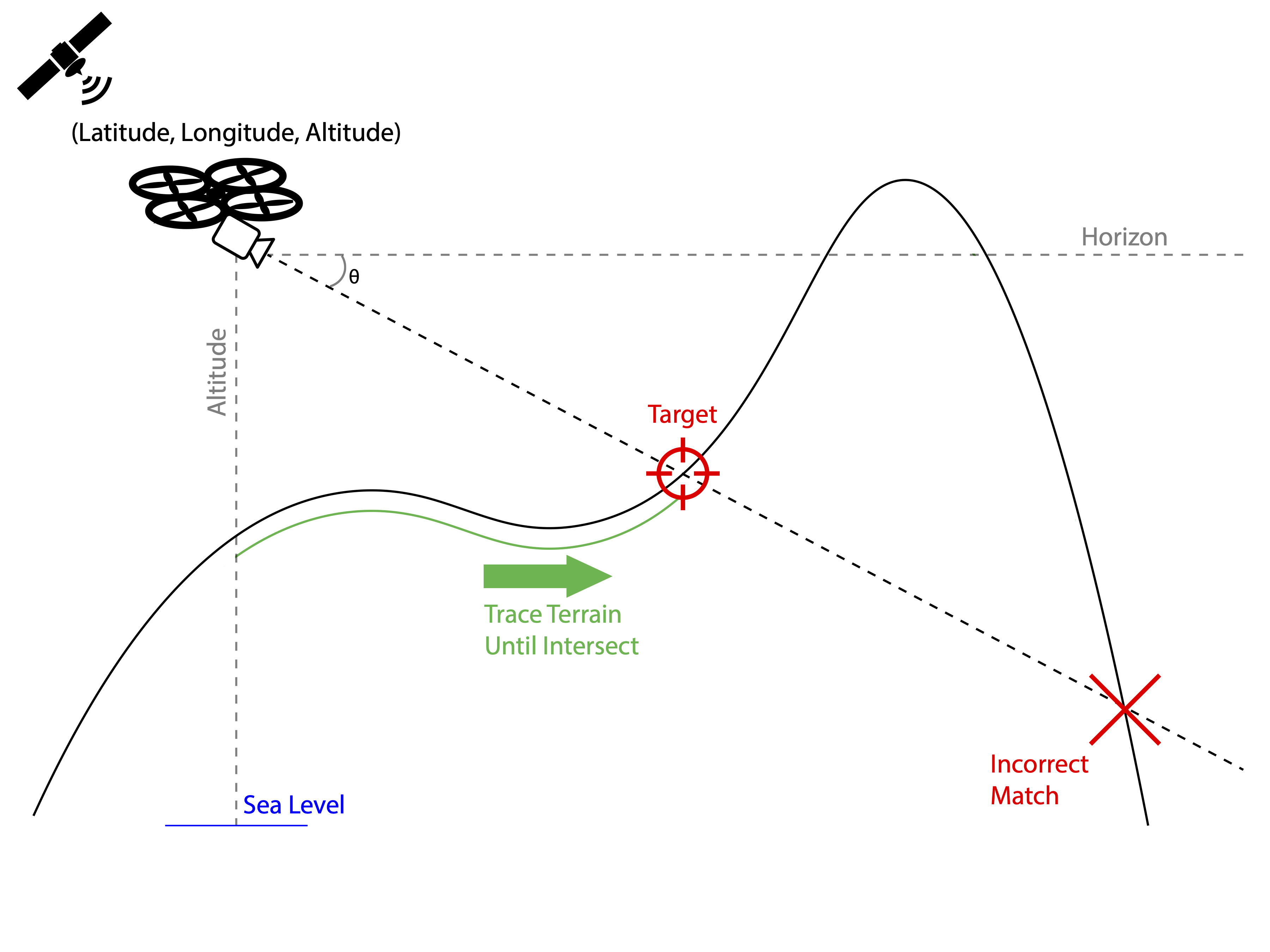
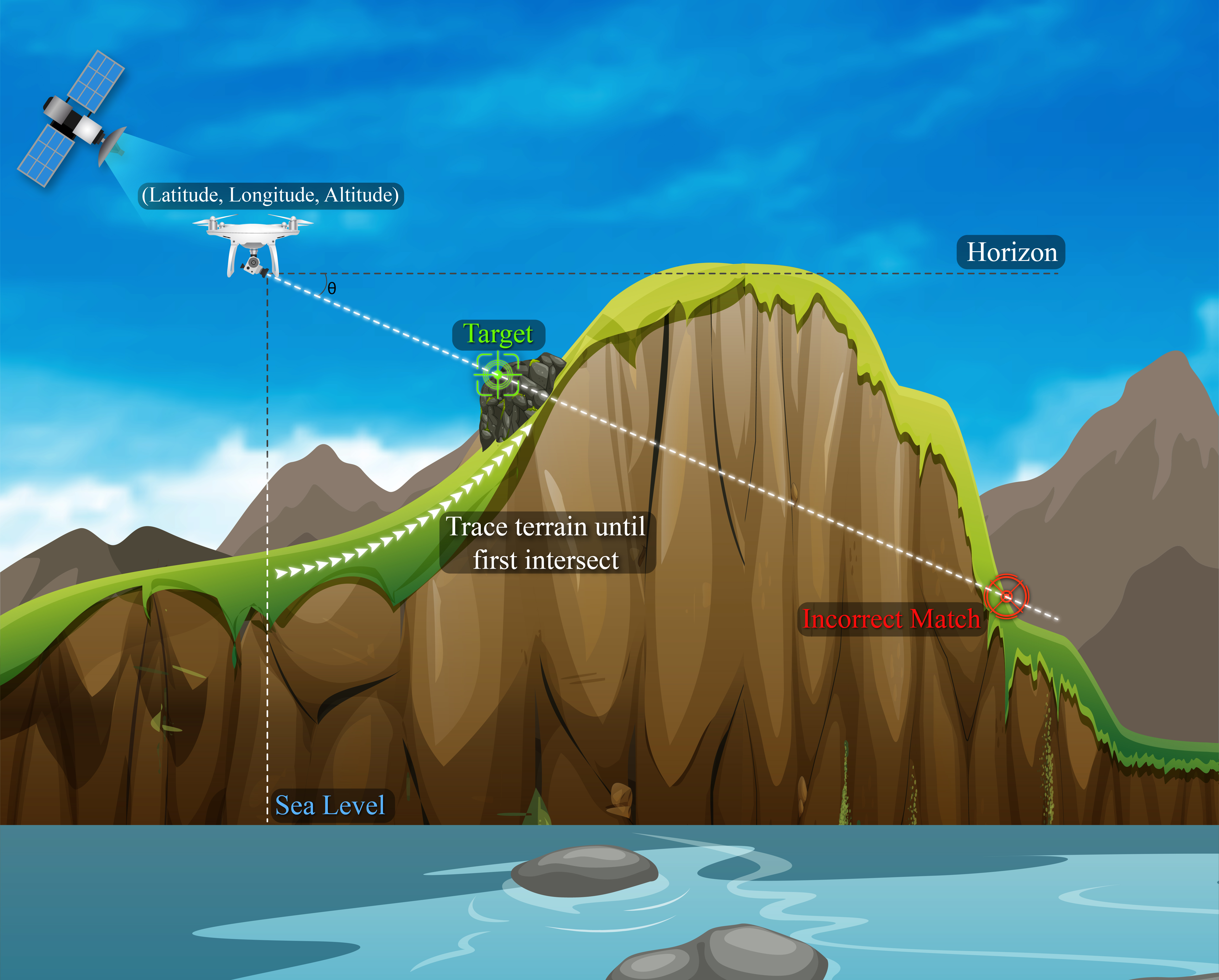
OpenAthena™ is a project which allows consumer and professional drones to spot precise locations through their images. This is accomplished by combining their sensor metadata with an offline-ready Digital Elevation Model to provide the instant location of what is being observed
🖼️👨💻 + 🧮⛰️ = 🎯📍
OpenAthena may prove especially useful for life-saving civilian search and rescue (SAR) and other commercial applications. For military use, this technique may greatly reduce the incidence of errors during the process of forward artillery observation. This may profoundly reduce harm to civilian lives and property in warfare.
This software is in pre-alpha. Use appropriate caution when using data generated from this program.
Looking for OpenAthena for Android? View that project here
While the importance of indirect fire (e.g. mortars, artillery, rockets) is well known to military historians, present-day soldiers, and others studied in methods of warfare, it remains a highly imprecise, blunt, and destructive tool. As such, it is used merely in a supporting role in today's combined arms doctrine.
Mastery of combined arms through maneuver warfare and air superiority remain the determinate factors of supremacy in current doctrine, preventing the effective application of indirect fire
As U.S. Army Chief of Staff Gen. Mark A. Milley wrote in the forward to U.S. Army Training and Doctrine Command Pamphlet 525-3-1, The U.S. Army in Multi-Domain Operations 2028: “emerging technologies” are “driving a fundamental change in the character of war.” They have “the potential to revolutionize battlefields unlike anything since the integration of machine guns, tanks, and aviation which began the era of combined arms warfare.”
Retired French army general Guy Hubin writes in Perspectives tactiques that the possibility of precision indirect fires is one such fundamental change in the character of war.
With recent advancements in consumer drone technology and publicly-available terrain datasets, a new possibility arises for doctrine. Inexpensive UAS aircraft may significantly enhance the capability of indirect fire. They can achieve this by improving indirect fire's accuracy and providing precise, immediate information on targets to operators of a broad range of existing weaponry.
Aerial forward artillery observation with small UAS's has proven to be very effective during the 2022 war in Ukraine
Examples:
In first-hand accounts (via reporter @Jack_Watling): shashj/status/1519041368672415747
In the news (via reporter @HoansSolo): HoansSolo/status/1523955057187860480
Against Armor: Blue_Sauron/status/1524742847664173057 kms_d4k/status/1524506214650028032
For counter-battery fire: Osinttechnical/status/1511867981596434434
For adjusting fall of shot: Osinttechnical/status/1516473926150463494
For disrupting combined arms offensives: UAWeapons/status/1509247556164935691
For disrupting logistics: Osinttechnical/status/1511683706511052808
This project anticipates that UAS's may enable a dramatic upset to established combined arms doctrine. Low cost unmaned aircraft are the instrument of such a change in the character of warfare. Such aircraft are easy to operate by infantry units and inexpensive to replace. Meanwhile, when used to guide indirect fire, such aircraft may provide an effective counter to concentrated infantry and armored units of an adversary fighting under current combined arms doctrine.
Due to the low altitude operation and inexpensive nature of such aircraft, they can counter concentrated combined arms forces even when higher-altitude air supremacy is not held or may not be achieved. In such a fashion, low altitude unmaned aircraft upset the role of high-altitude military aircraft as the only effective foil to ground-based combined arms.
Additionally, the combination of existing combined arms with new precision fire capabilities may allow a unit to move more rapidly and gain ground at frightening speeds using classic fire-and-movement tactics.
Precision indirect fire may suppress a target from beyond line of sight, reducing the burden of infantry to suppress a target while a friendly unit is in motion. Well-executed maneuvers under such conditions may out-pace a conventional force's ability to react, resupply, and reposition its own defenses.
Low altitude air supremacy must be considered equally as essential as that of high altitude in existing combined arms doctrine.
Infantry and armored units must guard against artillery-observing aircraft. Specialized low-altitude electronic countermeasures (ECM) must be developed. Such platforms should be able to deter such aircraft just as easily as they can be deployed
Effort should be made into producing inexpensive 'bird of prey' aircraft that can enforce low-altitude air supremacy and deny an adversary's aerial artillery observation
Consumer drones typically have an on-board 3D GPS sensor for position, a magnetometer (compass) for heading/azimuth, and a sensitive barometer (atmospheric pressure sensor) to enhance altitude accuracy.
They also typically have an "accelerometer" which allows it to stay level with the ground while in flight.
Importantly, such drones usually have a camera with a movable gimbal system.
The camera starts level with the horizon during normal operation, and the operator can pitch it downwards towards the ground for taking pictures. These pictures store GPS coordinates, altitude, and the azimuth and angle of depression downward (pitch) in their XMP and EXIF metadata (attached with the image)
Given that the lat/lon and altitude of the aircraft is known, its azimuth is known, and it is possible to obtain accurate worldwide elevation data (within ~30m) from this api, OpenAthena calculates the position and altitude of the terrain aimed at by the camera.
A constructed mathematical line (ray) is traced from the aircraft's camera towards the ground at its heading (azimuth) and angle of depression (theta) from the horizon. The point closest along this line yet reasonably near a geographic lat/lon/alt data point is usually the target which the camera is aiming at. This calculation provides the aircraft operator with a latitude, longitude, and elevation of the target to which the camera is aiming in an extremely short period of time.
Such a rapid positional resolution may prove ideal for many applications
This software is in pre-alpha. Use appropriate caution when using data generated from this program
Python3 (and the included pip package manager) must be installed first
Ensure your version of pip is up to date:
python3 -m pip install --upgrade pipNote: "python3" may just be called "python" depending on the configuration of your system
Then, download this repository to your computer (requires git):
git clone https://github.com/mkrupczak3/OpenAthena.git
cd OpenAthenaOnce inside the OpenAthena directory, install all pre-requisistes with pip:
python3 -m pip install -r requirements.txtthen run src/parseGeoTIFF.py with python3 to test your installation:
cd src
python3 parseGeoTIFF.py Rome-30m-DEM.tifYou should see output like this
If you encounter an error, please submit an issue to the Open Athena™ GitHub page
parseImage.py can perform automatic extraction and use of EXIF/XMP sensor metadata from drone photos. This allows for the automatic extraction and use of metadata including the aircraft camera's position, altitude, azimuth, and angle of depression (theta). OpenAthena (if provided terrain elevation data) will extract and use these values automaticaly to find the location on the ground in the exact center of the image
CAUTION: it is highly recommended that the aircraft's compass sensor is calibrated before each flight
More info here
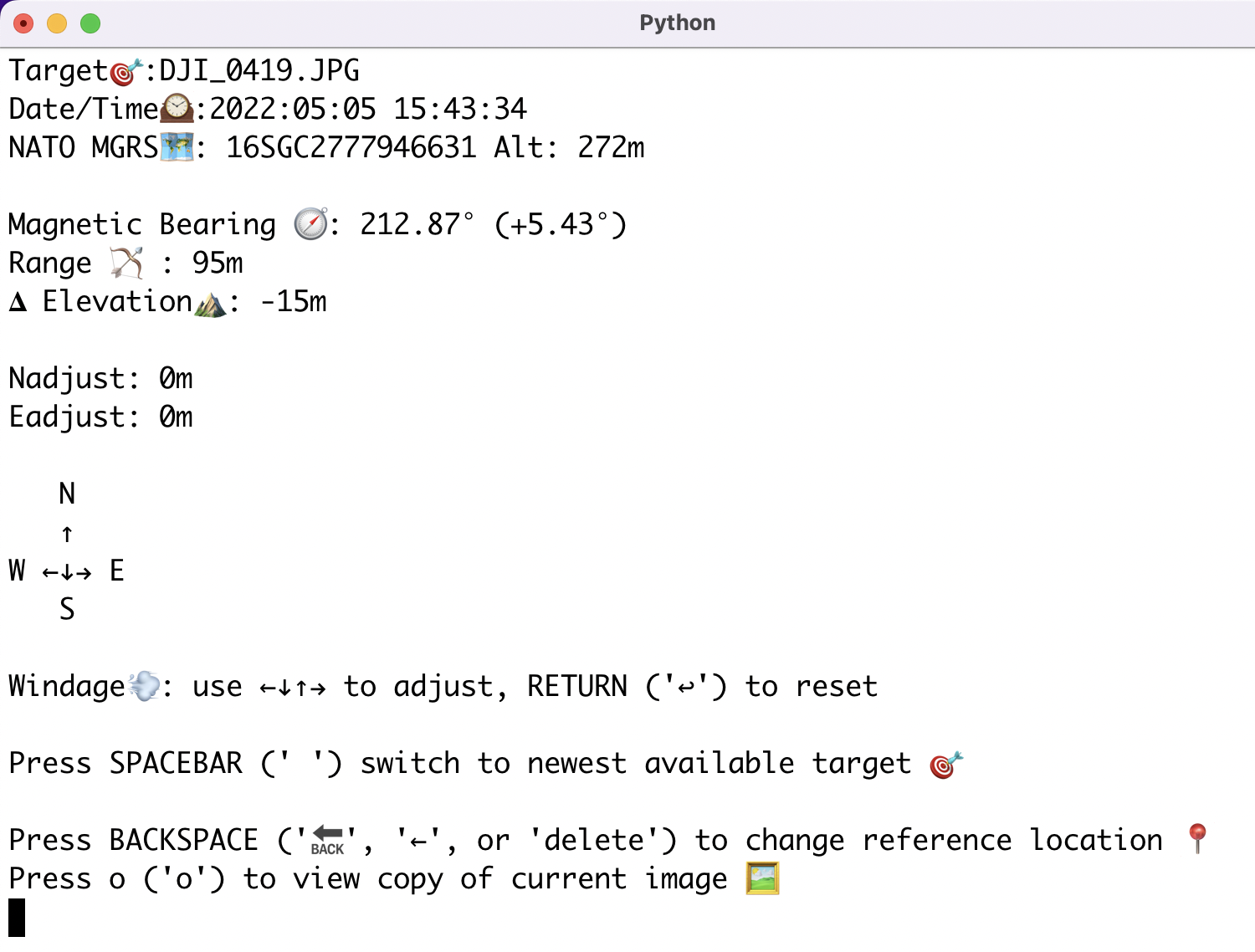
find_me_mode.py provides an alternate targeting mode where target match locations are provided in relative terms (bearing, distance, elevation change) from a fixed point. This may be useful for operators on the ground, including search and rescue teams, short-distance indirect fire teams (e.g. mortars) and the like
This mode is only intended for short range distances, otherwise it will be inaccurate (due to the curvature of the earth)
CAUTION: it is highly recommended that the aircraft's compass sensor is calibrated before each flight
More info here
Run python3 parseGeoTIFF.py (while in the src directory) for a demonstration of GeoTIFF DEM parsing. The file Rome-30m-DEM.tif is provided in the src directory as an example. A DEM covering a customized area can be easily obtained using the python elevation API
(counterintuitively, the x and y axis are backwards in the standard notation of a position via [latitude , longitude])
user@mypc:~/projects/OpenAthena/src$
python3 parseGeoTIFF.py
Then, exit the picture window that appears. You will now be prompted in the command line interface for a latitude and longitude. You may halt the program with Ctrl+C, otherwise you may enter lat/lon coordinates and the program will give you the position's terrain elevation using the previously displayed Digital Elevation Model.
getTarget.py performs the calculation for a terrain match from a constructed line
It has limited use for most users of this software, however it has an interactive mode available for demonstration
To start, cd into the src directory, then run getTarget.py:
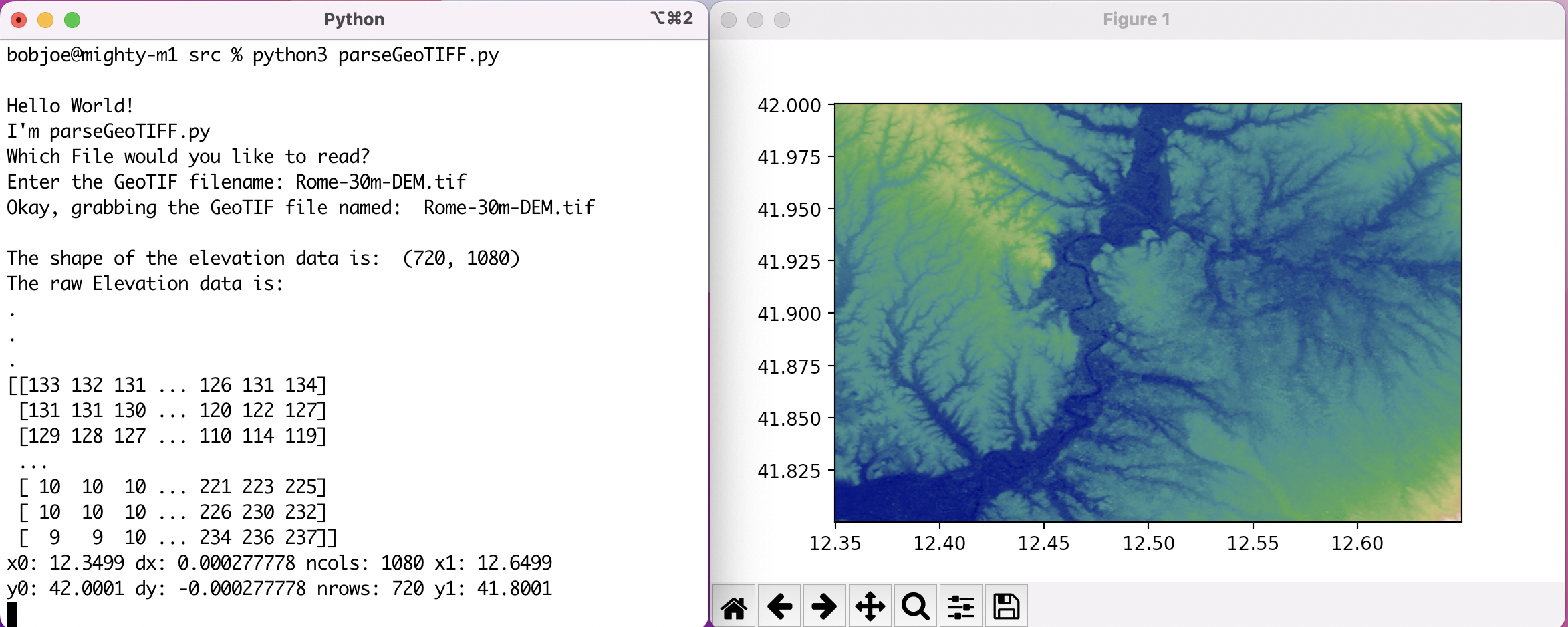
you@yourcomputer src % python3 getTarget.pyYou should then see the following prompt:
Hello World!
I'm getTarget.py
Which GeoTiff file would you like to read?
Enter the GeoTIFF filename:You can clip your own GeoTIFF file from the elevation API command line, or just use the provided example file Rome-30m-DEM.tif which contains the elevation data of the city of Rome, Italy and its outlying area
Hello World!
I'm getTarget.py
Which GeoTiff file would you like to read?
Enter the GeoTIFF filename: Rome-30m-DEM.tif[RETURN]
The shape of the elevation data is: (720, 1080)
The raw Elevation data is:
[[133 132 131 ... 126 131 134]
[131 131 130 ... 120 122 127]
[129 128 127 ... 110 114 119]
...
[ 10 10 10 ... 221 223 225]
[ 10 10 10 ... 226 230 232]
[ 9 9 10 ... 234 236 237]]
x0: 12.3499 dx: 0.000277778 ncols: 1080 x1: 12.6499
y0: 42.0001 dy: -0.000277778 nrows: 720 y1: 41.8001
Please enter aircraft latitude in (+/-) decimal form:The preceding numbers are provided for the user as debug information, but are not necessary during normal operation
Next, enter the latitude, then longitude, then altitude of the aircraft (standard WGS84):
Please enter aircraft latitude in (+/-) decimal form: 41.801
Please enter aircraft longitude in (+/-) decimal form: 12.6483
Please enter altitude (meters above mean sea level) in decimal form: 500
Please enter camera azimuth (0 is north) in decimal form (degrees):Next, enter the heading of the aircraft (in degrees, 0 is north and increasing clock-wise) and the angle of depression [theta] of the camera (in degrees, 0 is straight forward and increasing up to a maximum of 90 which is straight downwards)
Please enter camera azimuth (0 is north) in decimal form (degrees): 315
Please enter angle of declanation (degrees down from forward) in decimal form: 20
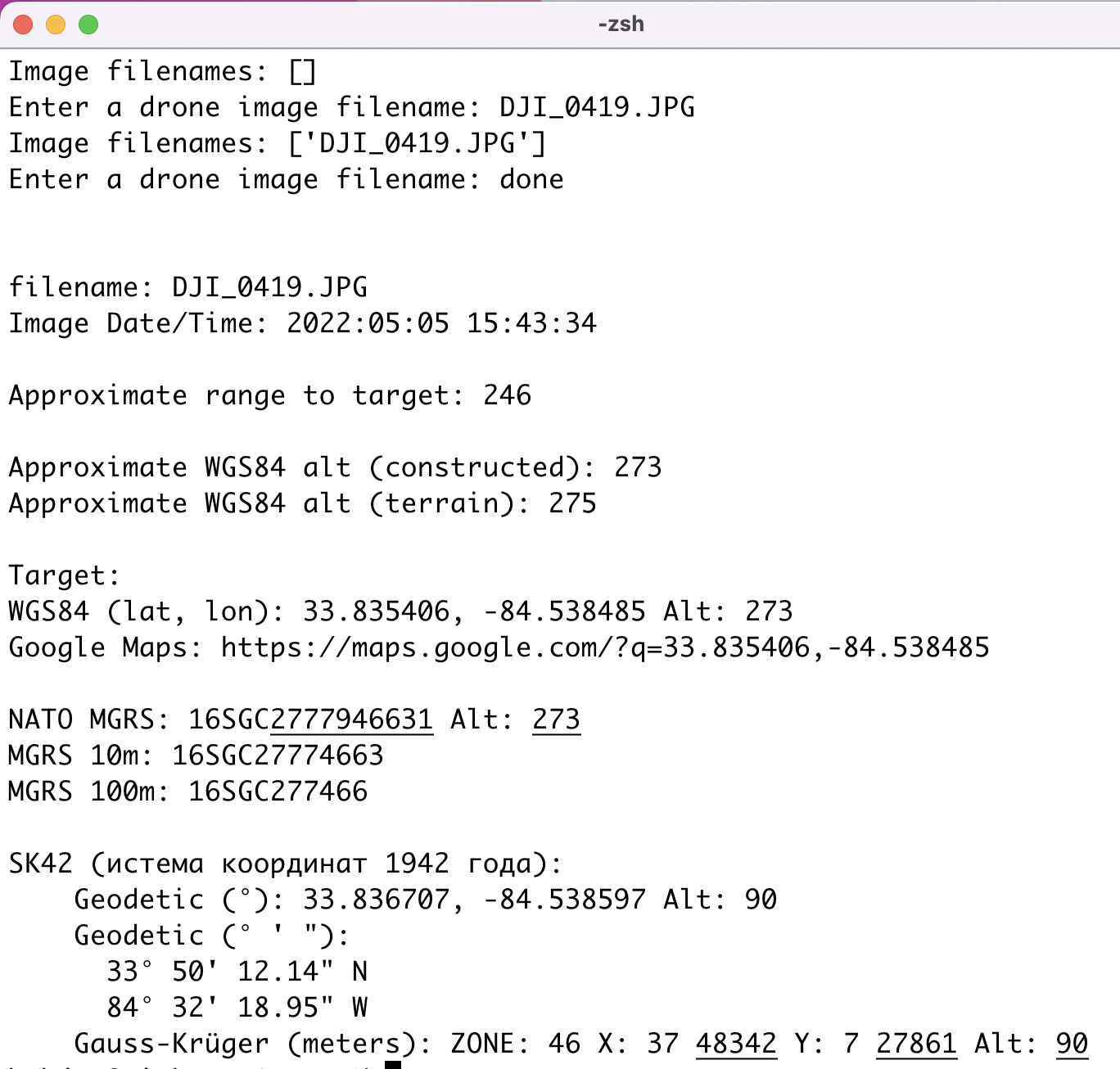
Approximate range to target: 1026
Approximate WGS84 alt (constructed): 150
Approximate alt (terrain): 147
Target:
WGS84 (lat, lon): 41.807133, 12.640073 Alt: 150
Google Maps: https://maps.google.com/?q=41.807133,12.640073
NATO MGRS: 33TUG0396131054 Alt: 150
MGRS 10m: 33TUG03963105
MGRS 100m: 33TUG039310
SK42 (истема координат 1942 года):
Geodetic (°): 41.807606, 12.641794 Alt: 99
Geodetic (° ' "):
41° 48' 27.38" N
12° 38' 30.46" E
Gauss-Krüger (meters): ZONE: 3 X: 46 33039 Y: 3 04024 Alt: 99
The distance of each iterative step, in meters, is defined by the increment variable in /src/config.py
The information in the following output lines represents the final positional resolution obtained by the approximate intersection of the constructed line emitted from the aircraft's camera and the ground as represented by the terrain data
The values should be tested for correctness
Approximate range to target: represents the direct-line distance in meters from the aircraft to the target. This may be useful for an operator to determine if the target match is in the expected place. To obtain the horizontal distance, multiply this number times the cosine of theta
Approximate alt (constructed) represents the aproximate altitude (meters above mean sea level) of the target according to the altitude of the last iteration along the constructed line
Approximate alt (terrain): represents the aproximate altitude (meters above mean sea level) of the target according to the terrain data points closest to the final lat./lon. pair
WGS84 (lat, lon): represents the latitude and longitude of the target to which the camera is likely aiming at. These values, in degrees, are from the common WGS84 coordinate system
Google Maps: a link to the previous lat/lon on Google Maps. Each rounded to 6 decimal places
NATO MGRS: represents the target location in the NATO Military Grid Reference System (MGRS), which is simmilar to UTM. The first 4 (or 5) digits defines the Grid Zone Designator (GZD). The next 10 digits represent the Grid Ref (1 meter square) of the target. The 10 digits of the grid, as well as the Altitude, are underlined in the output for easy reference.
MGRS 10m: same as NATO MGRS: except as an 8 digit (10m square) containing the target
MGRS 100m: same as MGRS 10m: except as a 6 digit (100m square) containing th target
SK42 (истема координат 1942 года): represents the target location according to the SK-42 (A.K.A. CK-42) coordinate system (Russian: Система координат 1942 года). This system is commonly used in old Soviet and post-Soviet style maps, and is based on a different ellipsoidal projection than WGS84 (called the Krassowsky 1940 ellipsoid)
Geodetic (°) represents the target location as latitude and longitude degrees outward from the center of the Krassowsky ellipsoid.
Geodetic (° ' ") The same value, split up into degrees, minutes, and seconds. Old Soviet style maps are commonly marked by degree (°) and minute (') on the axes as subscript.
Gauss-Krüger (meters): The same value, as a offest value (in meters)on a Gauss-Krüger projection. The last 5 digits of the offset Northing and Easting values are commonly used as grid labels on old Soviet style maps. "Northing" refers to a vertical line defined by an X value. "Easting" refers to a horizontal line defined by a Y value. ZONE specifies the GK longitudinal-zone (in 6° increments, possible values 1-60 inclusive). The smallest 5 digits of the Northing and Easting values, as well as the Altitude, are underlined in the output for easy reference.
The program getTarget.py will then exit
Especially when employed with precision smart munitions (e.g. artillery, aerial, etc.) this project will greatly aid the safety and processes of the forward artillery observer while reducing collateral damage. This technique attempts to minimize the risk of operator error (mismeasurement, miscalculation, etc.) and subsequent risk of friendly-fire and loss of civilian life.
In addition: a passive optical-based approach to target identification does not emit any signature which may forewarn a target or a group of targets (including armored vehicles). This may be highly beneficial depending on the usage environment.
This technology can be used for search and rescue operations, wildfire detection and management, measuring and surveying for civic engineering, and many other commercial purposes.
This software falls under the Dual Use Technology category under applicable U.S. arms export control laws. If you are using this software in a country that is under restriction from the United States under the Arms Export Control Act, you may only use this for civilian purposes and may not use this software in conflict. This author is not responsible for unauthorized usage of this open source project