alexandernst/javascript-algorithms

📝 Algorithms and data structures implemented in JavaScript with explanations and links to further readings

JavaScript Algorithms and Data Structures

🇺🇦 UKRAINE IS BEING ATTACKED BY RUSSIAN ARMY. CIVILIANS ARE GETTING KILLED. RESIDENTIAL AREAS ARE GETTING BOMBED.

• Help Ukraine via National Bank of Ukraine
• Help Ukraine via SaveLife fund
• More info on war.ukraine.ua and MFA of Ukraine

---

This repository contains JavaScript based examples of many popular algorithms and data structures.

Each algorithm and data structure has its own separate README with related explanations and links for further reading (including ones to YouTube videos).

Read this in other languages: 简体中文, 繁體中文, 한국어, 日本語, Polski, Français, Español, Português, Русский, Türkçe, Italiana, Bahasa Indonesia, Українська, Arabic, Tiếng Việt, Deutsch

☝ Note that this project is meant to be used for learning and researching purposes only, and it is not meant to be used for production.

Data Structures

A data structure is a particular way of organizing and storing data in a computer so that it can be accessed and modified efficiently. More precisely, a data structure is a collection of data values, the relationships among them, and the functions or operations that can be applied to the data.

B - Beginner, A - Advanced

• B Linked List
• B Doubly Linked List
• B Queue
• B Stack
• B Hash Table
• B Heap - max and min heap versions
• B Priority Queue
• A Trie
• A Tree
  • A Binary Search Tree
  • A AVL Tree
  • A Red-Black Tree
  • A Segment Tree - with min/max/sum range queries examples
  • A Fenwick Tree (Binary Indexed Tree)
• A Graph (both directed and undirected)
• A Disjoint Set - a union–find data structure or merge–find set
• A Bloom Filter
• A LRU Cache - Least Recently Used (LRU) cache

Algorithms

An algorithm is an unambiguous specification of how to solve a class of problems. It is a set of rules that precisely define a sequence of operations.

B - Beginner, A - Advanced

Algorithms by Topic

• Math
  • B Bit Manipulation - set/get/update/clear bits, multiplication/division by two, make negative etc.
  • B Binary Floating Point - binary representation of the floating-point numbers.
  • B Factorial
  • B Fibonacci Number - classic and closed-form versions
  • B Prime Factors - finding prime factors and counting them using Hardy-Ramanujan's theorem
  • B Primality Test (trial division method)
  • B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
  • B Least Common Multiple (LCM)
  • B Sieve of Eratosthenes - finding all prime numbers up to any given limit
  • B Is Power of Two - check if the number is power of two (naive and bitwise algorithms)
  • B Pascal's Triangle
  • B Complex Number - complex numbers and basic operations with them
  • B Radian & Degree - radians to degree and backwards conversion
  • B Fast Powering
  • B Horner's method - polynomial evaluation
  • B Matrices - matrices and basic matrix operations (multiplication, transposition, etc.)
  • B Euclidean Distance - distance between two points/vectors/matrices
  • A Integer Partition
  • A Square Root - Newton's method
  • A Liu Hui π Algorithm - approximate π calculations based on N-gons
  • A Discrete Fourier Transform - decompose a function of time (a signal) into the frequencies that make it up
• Sets
  • B Cartesian Product - product of multiple sets
  • B Fisher–Yates Shuffle - random permutation of a finite sequence
  • A Power Set - all subsets of a set (bitwise, backtracking, and cascading solutions)
  • A Permutations (with and without repetitions)
  • A Combinations (with and without repetitions)
  • A Longest Common Subsequence (LCS)
  • A Longest Increasing Subsequence
  • A Shortest Common Supersequence (SCS)
  • A Knapsack Problem - "0/1" and "Unbound" ones
  • A Maximum Subarray - "Brute Force" and "Dynamic Programming" (Kadane's) versions
  • A Combination Sum - find all combinations that form specific sum
• Strings
  • B Hamming Distance - number of positions at which the symbols are different
  • B Palindrome - check if the string is the same in reverse
  • A Levenshtein Distance - minimum edit distance between two sequences
  • A Knuth–Morris–Pratt Algorithm (KMP Algorithm) - substring search (pattern matching)
  • A Z Algorithm - substring search (pattern matching)
  • A Rabin Karp Algorithm - substring search
  • A Longest Common Substring
  • A Regular Expression Matching
• Searches
  • B Linear Search
  • B Jump Search (or Block Search) - search in sorted array
  • B Binary Search - search in sorted array
  • B Interpolation Search - search in uniformly distributed sorted array
• Sorting
  • B Bubble Sort
  • B Selection Sort
  • B Insertion Sort
  • B Heap Sort
  • B Merge Sort
  • B Quicksort - in-place and non-in-place implementations
  • B Shellsort
  • B Counting Sort
  • B Radix Sort
  • B Bucket Sort
• Linked Lists
  • B Straight Traversal
  • B Reverse Traversal
• Trees
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
• Graphs
  • B Depth-First Search (DFS)
  • B Breadth-First Search (BFS)
  • B Kruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
  • A Dijkstra Algorithm - finding the shortest paths to all graph vertices from single vertex
  • A Bellman-Ford Algorithm - finding the shortest paths to all graph vertices from single vertex
  • A Floyd-Warshall Algorithm - find the shortest paths between all pairs of vertices
  • A Detect Cycle - for both directed and undirected graphs (DFS and Disjoint Set based versions)
  • A Prim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
  • A Topological Sorting - DFS method
  • A Articulation Points - Tarjan's algorithm (DFS based)
  • A Bridges - DFS based algorithm
  • A Eulerian Path and Eulerian Circuit - Fleury's algorithm - Visit every edge exactly once
  • A Hamiltonian Cycle - Visit every vertex exactly once
  • A Strongly Connected Components - Kosaraju's algorithm
  • A Travelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
• Cryptography
  • B Polynomial Hash - rolling hash function based on polynomial
  • B Rail Fence Cipher - a transposition cipher algorithm for encoding messages
  • B Caesar Cipher - simple substitution cipher
  • B Hill Cipher - substitution cipher based on linear algebra
• Machine Learning
  • B NanoNeuron - 7 simple JS functions that illustrate how machines can actually learn (forward/backward propagation)
  • B k-NN - k-nearest neighbors classification algorithm
  • B k-Means - k-Means clustering algorithm
• Image Processing
  • B Seam Carving - content-aware image resizing algorithm
• Statistics
  • B Weighted Random - select the random item from the list based on items' weights
• Evolutionary algorithms
  • A Genetic algorithm - example of how the genetic algorithm may be applied for training the self-parking cars
• Uncategorized
  • B Tower of Hanoi
  • B Square Matrix Rotation - in-place algorithm
  • B Jump Game - backtracking, dynamic programming (top-down + bottom-up) and greedy examples
  • B Unique Paths - backtracking, dynamic programming and Pascal's Triangle based examples
  • B Rain Terraces - trapping rain water problem (dynamic programming and brute force versions)
  • B Recursive Staircase - count the number of ways to reach to the top (4 solutions)
  • B Best Time To Buy Sell Stocks - divide and conquer and one-pass examples
  • A N-Queens Problem
  • A Knight's Tour

Algorithms by Paradigm

An algorithmic paradigm is a generic method or approach which underlies the design of a class of algorithms. It is an abstraction higher than the notion of an algorithm, just as an algorithm is an abstraction higher than a computer program.

• Brute Force - look at all the possibilities and selects the best solution
  • B Linear Search
  • B Rain Terraces - trapping rain water problem
  • B Recursive Staircase - count the number of ways to reach to the top
  • A Maximum Subarray
  • A Travelling Salesman Problem - shortest possible route that visits each city and returns to the origin city
  • A Discrete Fourier Transform - decompose a function of time (a signal) into the frequencies that make it up
• Greedy - choose the best option at the current time, without any consideration for the future
  • B Jump Game
  • A Unbound Knapsack Problem
  • A Dijkstra Algorithm - finding the shortest path to all graph vertices
  • A Prim’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
  • A Kruskal’s Algorithm - finding Minimum Spanning Tree (MST) for weighted undirected graph
• Divide and Conquer - divide the problem into smaller parts and then solve those parts
  • B Binary Search
  • B Tower of Hanoi
  • B Pascal's Triangle
  • B Euclidean Algorithm - calculate the Greatest Common Divisor (GCD)
  • B Merge Sort
  • B Quicksort
  • B Tree Depth-First Search (DFS)
  • B Graph Depth-First Search (DFS)
  • B Matrices - generating and traversing the matrices of different shapes
  • B Jump Game
  • B Fast Powering
  • B Best Time To Buy Sell Stocks - divide and conquer and one-pass examples
  • A Permutations (with and without repetitions)
  • A Combinations (with and without repetitions)
  • A Maximum Subarray
• Dynamic Programming - build up a solution using previously found sub-solutions
  • B Fibonacci Number
  • B Jump Game
  • B Unique Paths
  • B Rain Terraces - trapping rain water problem
  • B Recursive Staircase - count the number of ways to reach to the top
  • B Seam Carving - content-aware image resizing algorithm
  • A Levenshtein Distance - minimum edit distance between two sequences
  • A Longest Common Subsequence (LCS)
  • A Longest Common Substring
  • A Longest Increasing Subsequence
  • A Shortest Common Supersequence
  • A 0/1 Knapsack Problem
  • A Integer Partition
  • A Maximum Subarray
  • A Bellman-Ford Algorithm - finding the shortest path to all graph vertices
  • A Floyd-Warshall Algorithm - find the shortest paths between all pairs of vertices
  • A Regular Expression Matching
• Backtracking - similarly to brute force, try to generate all possible solutions, but each time you generate next solution you test if it satisfies all conditions, and only then continue generating subsequent solutions. Otherwise, backtrack, and go on a different path of finding a solution. Normally the DFS traversal of state-space is being used.
  • B Jump Game
  • B Unique Paths
  • B Power Set - all subsets of a set
  • A Hamiltonian Cycle - Visit every vertex exactly once
  • A N-Queens Problem
  • A Knight's Tour
  • A Combination Sum - find all combinations that form specific sum
• Branch & Bound - remember the lowest-cost solution found at each stage of the backtracking search, and use the cost of the lowest-cost solution found so far as a lower bound on the cost of a least-cost solution to the problem, in order to discard partial solutions with costs larger than the lowest-cost solution found so far. Normally BFS traversal in combination with DFS traversal of state-space tree is being used.

How to use this repository

Install all dependencies

npm install

Run ESLint

You may want to run it to check code quality.

npm run lint

Run all tests

npm test

Run tests by name

npm test -- 'LinkedList'

Troubleshooting

If linting or testing is failing, try to delete the node_modules folder and re-install npm packages:

rm -rf ./node_modules
npm i

Also make sure that you're using a correct Node version (>=16). If you're using nvm for Node version management you may run nvm use from the root folder of the project and the correct version will be picked up.

Playground

You may play with data-structures and algorithms in ./src/playground/playground.js file and write tests for it in ./src/playground/__test__/playground.test.js.

Then just simply run the following command to test if your playground code works as expected:

npm test -- 'playground'

Useful Information

References

• ▶ Data Structures and Algorithms on YouTube
• ✍🏻 Data Structure Sketches

Big O Notation

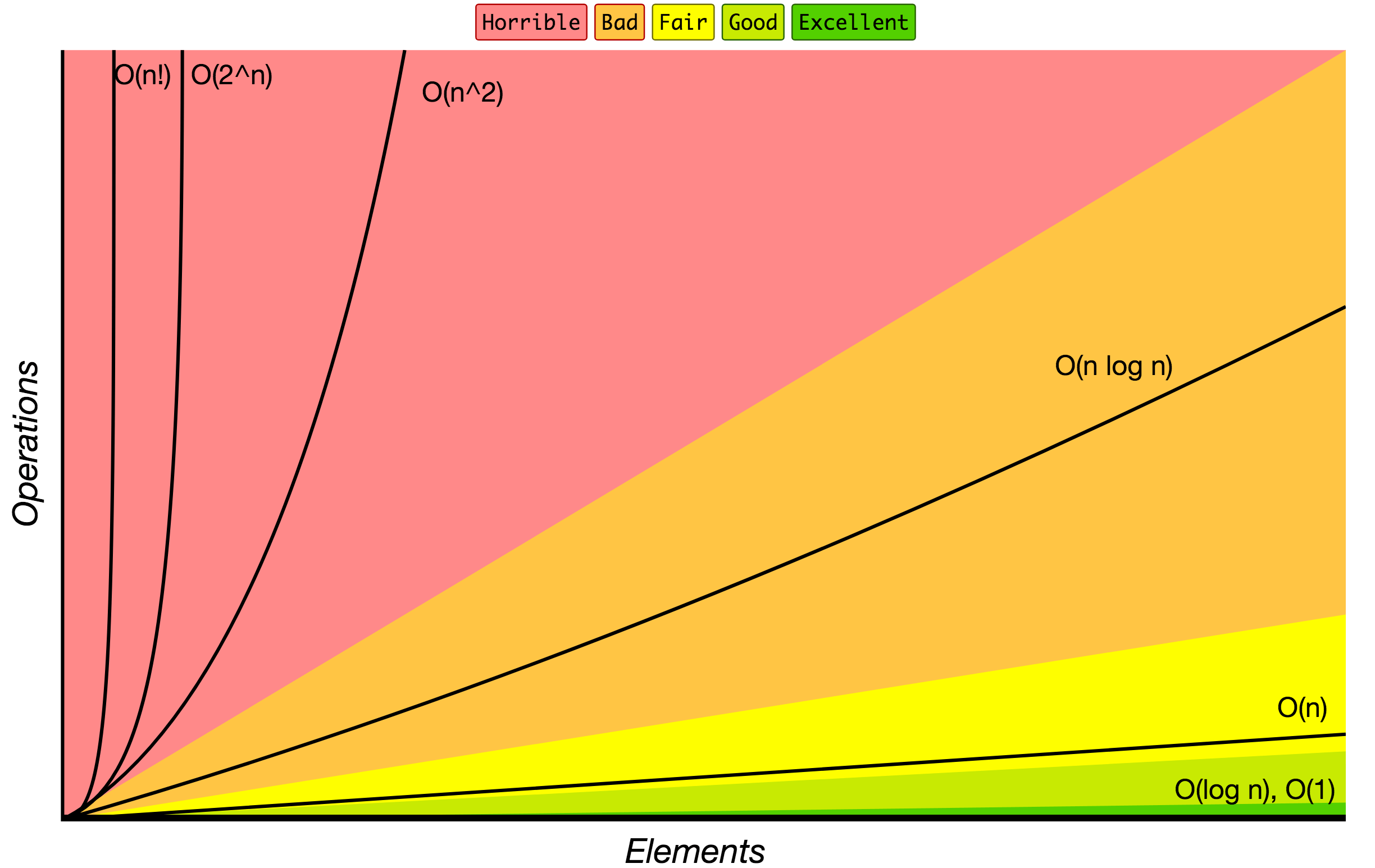
Big O notation is used to classify algorithms according to how their running time or space requirements grow as the input size grows. On the chart below you may find most common orders of growth of algorithms specified in Big O notation.

Source: Big O Cheat Sheet.

Below is the list of some of the most used Big O notations and their performance comparisons against different sizes of the input data.

Big O Notation	Type	Computations for 10 elements	Computations for 100 elements	Computations for 1000 elements
O(1)	Constant	1	1	1
O(log N)	Logarithmic	3	6	9
O(N)	Linear	10	100	1000
O(N log N)	n log(n)	30	600	9000
O(N^2)	Quadratic	100	10000	1000000
O(2^N)	Exponential	1024	1.26e+29	1.07e+301
O(N!)	Factorial	3628800	9.3e+157	4.02e+2567

Data Structure Operations Complexity

Data Structure	Access	Search	Insertion	Deletion	Comments
Array	1	n	n	n
Stack	n	n	1	1
Queue	n	n	1	1
Linked List	n	n	1	n
Hash Table	-	n	n	n	In case of perfect hash function costs would be O(1)
Binary Search Tree	n	n	n	n	In case of balanced tree costs would be O(log(n))
B-Tree	log(n)	log(n)	log(n)	log(n)
Red-Black Tree	log(n)	log(n)	log(n)	log(n)
AVL Tree	log(n)	log(n)	log(n)	log(n)
Bloom Filter	-	1	1	-	False positives are possible while searching

Array Sorting Algorithms Complexity

Name	Best	Average	Worst	Memory	Stable	Comments
Bubble sort	n	n2	n2	1	Yes
Insertion sort	n	n2	n2	1	Yes
Selection sort	n2	n2	n2	1	No
Heap sort	n log(n)	n log(n)	n log(n)	1	No
Merge sort	n log(n)	n log(n)	n log(n)	n	Yes
Quick sort	n log(n)	n log(n)	n2	log(n)	No	Quicksort is usually done in-place with O(log(n)) stack space
Shell sort	n log(n)	depends on gap sequence	n (log(n))2	1	No
Counting sort	n + r	n + r	n + r	n + r	Yes	r - biggest number in array
Radix sort	n * k	n * k	n * k	n + k	Yes	k - length of longest key

Project Backers

You may support this project via ❤️️ GitHub or ❤️️ Patreon.

Folks who are backing this project ∑ = 1

Author

@trekhleb

A few more projects and articles about JavaScript and algorithms on trekhleb.dev