Big O. Time and Space complexity.
In Computer Science and Programming the way in which we measure the performance and efficiency of algorithms is using Big O notation, denoted O().
Some rules when calculating Big O:
- Different steps when not nested gets added.
- Nested steps gets multiplied, pay close attention to the collection variable name.
- We drop the constants as we are only concerned with how the algorithm scales with repect to the runtime.
- If the inputs are different, we use different variable names.
- In an algorithm we drop the non-dominant terms e.g
O(n + n ^ 2)becomesO(n ^ 2).
Runtime complexity is used to describe the efficiency of a given algorithm as the size of the input grows.
| Big O Notation | Name |
|---|---|
| O(1) | constant |
| O(log n) | logarithmic |
| O(n) | linear |
| O(n log n) | linearithmic |
| O(n ^ 2) | quadratic |
| O(n ^ 3) | cubic |
| O(n ^ y) | polynomial |
| O(2 ^ n) | exponential |
| O(n!) | factorial |
Swift Playgrounds with some runtime examples
In the example below the runtime complexity of calculateAverageAge is O(n), read (big O of n). As the size of the ages array grows the efficiency of this algorithm grows linearly.
It is O(n) since we are iterating through each element, represented as n in the ages array. n is the length of the array.
func calculateAverageAge(_ ages: [Int]) -> Double {
var sumOfAges = 0
for age in ages {
sumOfAges += age
}
return Double(sumOfAges / ages.count)
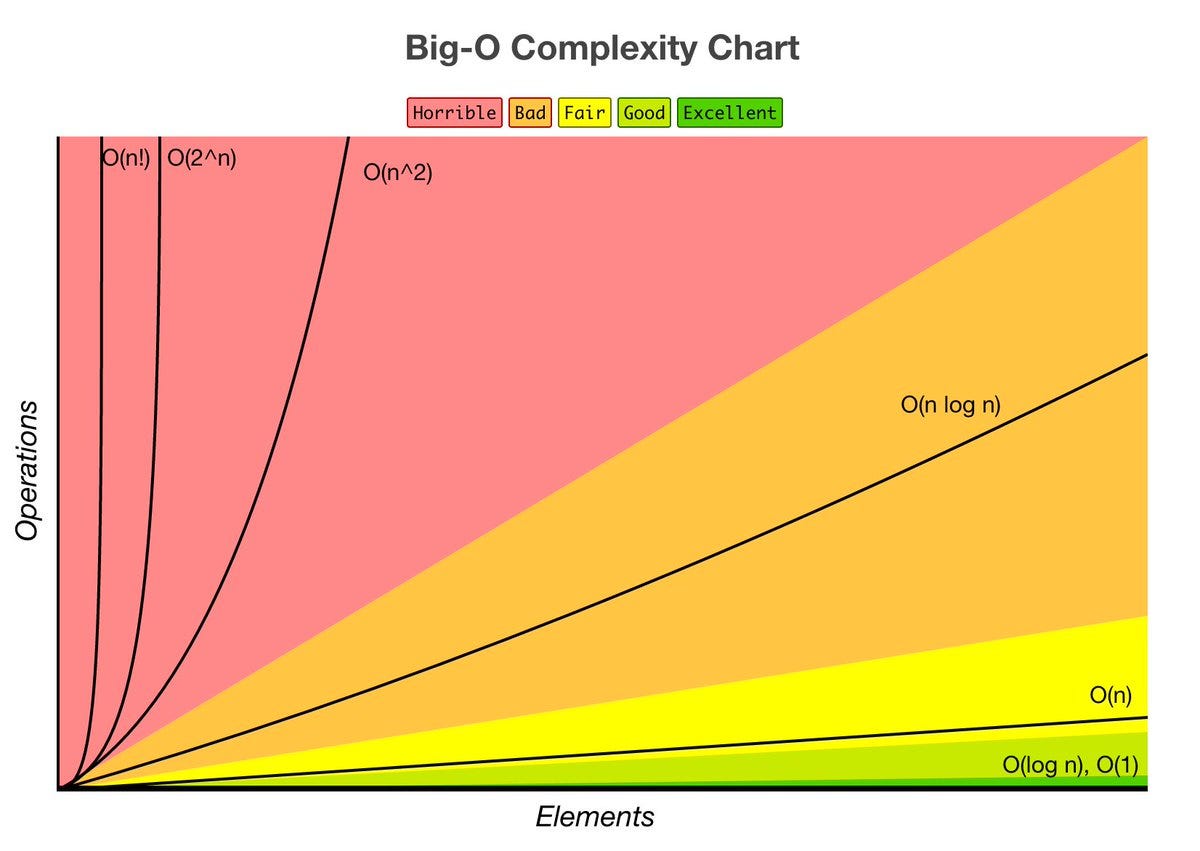
}The Big O chart below shows common runtime complexities.
In this example the runtimes are added because we finish the work of the first for loop before running the second for loop.
So we conclude that this runtime is O(A + B). We use the variables A and B to represent each array since they are different. If the two arrays were the same the runtime would be for example A + A which would be O(A) since we ignore constants.
func compoundFuncOne(_ arrA: [Int], _ arrB: [Int]) {
for num in arrA {
print(num)
}
for num in arrB {
print(num)
}
}In this example we perform work in the inner for loop for every element in the outer for loop therefore we multiply the runtimes.
The runtime becomes O(A * B) or O(AB).
func compoundFuncTwo(_ arrA: [Int], _ arrB: [Int]) {
for a in arrA {
for b in arrB {
print("\(a) + \(b)")
}
}
}One of the best examples of O(log n) runtime is binary search, where the given sorted array is cut in half on each search.
Similar algorithms that divides problems in halves like merge sort, quicksort do have O(log n) runtime in their final runtimes but since more work is involved those end up with O(n log n) runtimes.
In calculating Big O runtimes we drop the constants.
Below the given runtime is O(n + n) or O(2n) or better written as O(n) since we ignore constants in runtime calculations.
let names = ["Alex", "Paul"]
for char in names {
print(char.lowercased())
}
for char in names {
print(char.uppercased())
}O(n)
O(1)
O(n log n)
O(n)
Space complexity is defined as the amount of memory needed for a given algorithm. As the input size of an algorithm increases the amount of space increases accordingly.
Auxiliary space is extra space or temporary space used by the algorithms during its execution.
| Type | Bit Width | Range |
|---|---|---|
| Int8 | 1byte | -127 to 127 |
| UInt8 | 1byte | 0 to 255 |
| Int32 | 4bytes | -2147483648 to 2147483647 |
| UInt32 | 4bytes | 0 to 4294967295 |
| Int64 | 8bytes | -9223372036854775808 to 9223372036854775807 |
| UInt64 | 8bytes | 0 to 18446744073709551615 |
| Float | 4bytes | 1.2E-38 to 3.4E+38 (~6 digits) |
| Double | 8bytes | 2.3E-308 to 1.7E+308 (~15 digits) |
Note: If you're on a 64-bit platform, Int is the same size a Int64. You can try this in playgrounds by running
print(Int.max). On my machine the output is9223372036854775807.
let intValue = 10
let intSize = MemoryLayout.size(ofValue: intValue) // 8 bytes
MemoryLayout<Int>.size // 8
MemoryLayout<Double>.size // 8
MemoryLayout<Float>.size // 4
MemoryLayout<Int8>.size // 1
MemoryLayout<String>.size // 16Here the add(:_) function takes two inputs of type Int and returns and Int. Each of those variables take up constant memory or 8 bytes each on a 64-bit platform like macOS, we calculate the space each variable takes which is 8 bytes from variable a + 8 bytes for variable b which sums up to 16 bytes, therefore when concluding the big O complexities we ignore constants and get a space complexity of O(1).
func add(_ a: Int, _ b: Int) -> Int {
return a + b
}The addSavings(:_) function takes an input array savings and iterates this array for each Double element it contains, since this array is not a constant and has n elements we have to consider this when calculating space complexity, therefore we conclude that the amount of memory it takes for the given algorithm is O(n).
Space complexity calculation: size of array * memory per element, n * 8 bytes, since we ignore the constant the space complexity is O(n).
func addSavings(_ savings: [Double]) -> Double {
var sum = 0.0
for saving in savings {
sum += saving
}
return sum
}In this example the sum(_:) function is being called recursively and decrementing the value of k until it reaches the base case of 0 and returns the value from the call stack. Here the runtime complexity is O(n) as we count how many times the recursive call happens and the space complexity is also O(n) as it takes space on the call stack.
func recursionSum(_ k: Int) -> Int {
guard k > 0 else {
return 0
}
return k + recursionSum(k - 1)
}
recursionSum(5) // 5 + 4 + 3 + 2 + 1 = 15Call Stack
recursionSum(5)
=> recursionSum(4)
=> recursionSum(3)
=> recursionSum(2)
=> recursionSum(1)
=> recursionSum(0)
In this example though we are calling pairSum() n times, the calls do not remain on the call stack like in recursionSum(:_) so here the space complexity is constant O(1).
func pairSumSequence(_ k: Int) -> Int {
var sum = 0
for i in 0..<k {
sum += pairSum(i, i + 1)
}
return sum
}
func pairSum(_ a: Int, _ b: Int) -> Int {
return a + b
}
pairSumSequence(3) // 9What is the runtime complexity of the given algorithm?
func sumProduct(_ arr: [Int]) {
var sum = 0
var product = 1
for num in arr {
sum += num
}
for num in arr {
product *= num
}
print("sum is \(sum), and product is \(product)")
}Solution
O(n) because we add the runtimes and since both for loops are iterating through the same array denoted a n it is O(n)
What is the runtime complexity of the given algorithm?
func printPairs(_ arr: [Int]) {
for i in 0..<arr.count {
for j in 0..<arr.count {
print("\(arr[i]), \(arr[j])")
}
}
}Solution
O(n ^ 2) here the first for loop calls the inner for loop on each of it's elements, so we multiply the runtimes. Since both are the same collection and we use n to represent the collection we say the runtime is n * n or O(n ^ 2).
What is the runtime complexity of the given algorithm?
func printUnorderedPairs(_ arrA: [Int], _ arrB: [Int]) {
for i in 0..<arrA.count {
for j in 0..<arrB.count {
if arrA[i] < arrB[j] {
print("\(arrA[i]), \(arrB[j])")
}
}
}
}Solution
O(ab), here since we have two different arrays a and b we treat the runtime using different variables a and b. As before we multiply such runtimes where the for loops are nested and result to a runtime of O(a * b) or O(ab).
What is the runtime complexity of the given algorithm?
func printUnorderedPairs(_ arrA: [Int], _ arrB: [Int]) {
for i in 0..<arrA.count {
for j in 0..<arrB.count {
for k in 0..<100 {
if arrA[i] < arrB[j] {
print("\(arrA[i]), \(arrB[j]), \(k)")
}
}
}
}
}Solution
The runtime is O(ab) regardless of the third for loop, remember when it comes to calculating runtimes that we drop the constants.
What is the runtime complexity of the given algorithm?
func firstHalf(_ arr: [Int]) {
for i in 0..<arr.count / 2 {
print(arr[i])
}
}Solution
The runtime is O(n) despite the fact that we only iterate through first half of the array.
You are looking for a specific value in a binary tree, but the tree is not a binary search tree. What is the runtime complexity?
Solution
If the tree is not a BST, then worst case is you have to visit each node making it a runtime of O(n).
What is the runtime complexity of the given algorithm?
func product(_ a: Int, _ b: Int) -> Int {
var sum = 0
for _ in 0..<b {
sum += a
}
return sum
}Solution
The runtime in this example is O(b).
What is the runtime complexity of the given algorithm?
func power(_ a: Int, _ b: Int) -> Int {
if b < 0 { return 0 }
else if b == 0 { return 1 }
else {
return a * power(a, b - 1)
}
}Solution
In this recursive call, at each call to power(:_) b is decremented by 1, thus we conclude that the call stack add n calls and the runtime is O(n).
What is the space complexity of the given algorithm?
func addNumbers(a: Int, b: Int, c: Int) -> Int {
return a + b + c
}Solution
Space complexity is O(1). a + b + c or 8 bytes + 8 bytes + 8 bytes = 24 bytes, we ignore constants as with calculating runtime and get a constant space complexity.
What is the space complexity of the given algorithm?
func calculateShoppingCart(prices: [Double]) -> Double {
var totalPrice = 0.0
for price in prices {
totalPrice += price
}
return totalPrice
}Solution
Here we have an array of Double, the size of a Double is 8 bytes. The array has n elements. If we calculate each element's space needed for the for loop we see that n (size of array) * 8 bytes equates to a space complexity of O(n * 8 bytes) or O(n) again as we ignore the constant space taken.
What is the space complexity of the given algorithm?
func square(_ value: Int) -> Int {
return value * value
}Solution
O(1)
What is the space complexity of the given algorithm?
func sayHiNTimes(_ k: Int) {
guard k > 0 else {
print("Be polite")
return
}
for _ in 0..<k {
print("hi")
}
}Solution
This algorithim is not taking up extra memory than supplied by the input. The input passed in is a constant, k of type Int which takes up 8 bytes and we disregard in our space complexity calculations, therefore the space complexity is O(1).
What is the space complexity of the given algorithm?
func listOfHiTimes(_ k: Int) -> [Int] {
guard k > 0 else { return [] }
var list = [Int]()
for i in 0..<k {
list.append(i)
}
return list
}Solution
In this example the variable list array scales linearlly with the size of the input k which consumes memory inside the for loop when values are appending to it. Here the space complexity is O(n).
What is the space complexity of the given algorithm?
func printList(_ list: [Int]) {
for i in 0..<list.count {
for j in 0..<list.count {
print("\(list[i]), \(list[j])")
}
}
}Solution
In this example no auxillary space is used by the printList(:_) function. Recall we do not count the input's memory footprint when calculating space complexity. We conclude that the space complexity is O(1).
What is the space complexity of the given algorithm?
func inputSize(_ size: Int) {
var arr = [Int]()
for i in 0..<size {
arr.append(i)
}
print(arr)
}Solution
An array of size n has been allocated in the inputSize(_:) function, when we calculate the memory footprint we see that n * 8 bytes results in a space complexity of O(n).
- Big O Cheatsheet
- Understanding Space Complexity
- Interview Cake - Big O Notation
- moducode - Time & Space Complexity in Functions – Big O Notation