Quantum signal processing is a framework for quantum algorithms including Hamiltonian simulation, quantum linear system solving, amplitude amplification, etc.
Quantum signal processing performs spectral transformation of any unitary
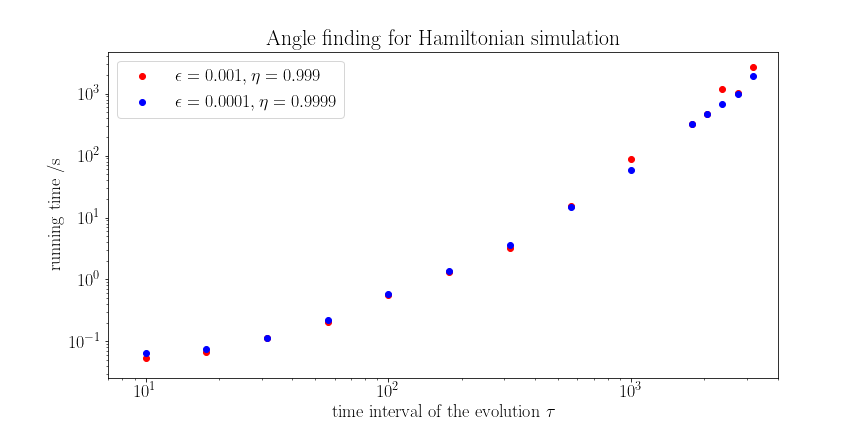
Our software package provides a lightweight solution for classically solving for the single-qubit rotation angles given the Laurent polynomial, a task called angle sequence finding or angle finding. Our package only depends on numpy and scipy and works under machine precision. Please see below for a chart giving the performance of our algorithm for the task of Hamiltonian simulation:
Please see the arXiv manuscript for more details.
-
angle_sequence.pyis the main module of the algorithm. -
LPoly.pydefines two classesLPolyandLAlg, representing Laurent polynomials and Low algebra elements respectively. -
completion.pydescribes the completion algorithm: Given a Laurent polynomial element$F(\tilde{w})$ , find its counterpart$G(\tilde{w})$ such that$F(\tilde{w})+G(\tilde{w})*iX$ is a unitary element. -
decomposition.pydescribes the halving algorithm: Given a unitary parity Low algebra element$V(\tilde{w})$ , decompose it as a unique product of degree-0 rotations$\exp{i\theta X}$ and degree-1 monomials$w$ . -
ham_sim.pyshows an example of how the angle sequence for Hamiltonian simulation can be found.
To find the angle sequence corresponding to a real Laurent polynomial
from angle_sequence import angle_sequence
ang_seq = angle_sequence([a_{-n}, a_{-n+2}, ..., a_n])
print(ang_seq)
- Rui Chao, Dawei Ding, András Gilyén, Cupjin Huang, and Mario Szegedy. Finding Angles for Quantum Signal Processing with Machine Precision. arXiv preprint arXiv:2003.02831 (2020).