In this project, you will evaluate the performance and predictive power of a model that has been trained and tested on data collected from homes in suburbs of Boston, Massachusetts. A model trained on this data that is seen as a good fit could then be used to make certain predictions about a home — in particular, its monetary value. This model would prove to be invaluable for someone like a real estate agent who could make use of such information on a daily basis.
The dataset for this project originates from the UCI Machine Learning Repository. The Boston housing data was collected in 1978 and each of the 506 entries represent aggregated data about 14 features for homes from various suburbs in Boston, Massachusetts. For the purposes of this project, the following preprocessing steps have been made to the dataset:
- 16 data points have an
'MDEV'value of 50.0. These data points likely containmissing or censored values and have been removed. - 1 data point has an
'RM'value of 8.78. This data point can be considered anoutlier and has been removed. - The features
'RM','LSTAT','PTRATIO', and'MDEV'are essential. The remainingnon-relevant features have been excluded. - The feature
'MDEV'has beenmultiplicatively scaled to account for 35 years of market inflation.
Run the code cell below to load the Boston housing dataset, along with a few of the necessary Python libraries required for this project. You will know the dataset loaded successfully if the size of the dataset is reported.
# Import libraries necessary for this project
import numpy as np
import pandas as pd
import visuals as vs # Supplementary code
from sklearn.cross_validation import ShuffleSplit
# Pretty display for notebooks
%matplotlib inline
# Load the Boston housing dataset
data = pd.read_csv('housing.csv')
prices = data['MDEV']
features = data.drop('MDEV', axis = 1)
# Success
print "Boston housing dataset has {} data points with {} variables each.".format(*data.shape)Boston housing dataset has 489 data points with 4 variables each.
In this first section of this project, you will make a cursory investigation about the Boston housing data and provide your observations. Familiarizing yourself with the data through an explorative process is a fundamental practice to help you better understand and justify your results.
Since the main goal of this project is to construct a working model which has the capability of predicting the value of houses, we will need to separate the dataset intofeatures and thetarget variable. Thefeatures, 'RM', 'LSTAT', and 'PTRATIO', give us quantitative information about each data point. Thetarget variable, 'MDEV', will be the variable we seek to predict. These are stored in features and prices, respectively.
For your very first coding implementation, you will calculate descriptive statistics about the Boston housing prices. Since numpy has already been imported for you, use this library to perform the necessary calculations. These statistics will be extremely important later on to analyze various prediction results from the constructed model.
In the code cell below, you will need to implement the following:
- Calculate the minimum, maximum, mean, median, and standard deviation of
'MDEV', which is stored inprices.- Store each calculation in their respective variable.
# Minimum price of the data
minimum_price = np.min(prices)
# Maximum price of the data
maximum_price = np.max(prices)
# Mean price of the data
mean_price = np.mean(prices)
# Median price of the data
median_price = np.median(prices)
# Standard deviation of prices of the data
std_price = np.std(prices)
# Show the calculated statistics
print "Statistics for Boston housing dataset:\n"
print "Minimum price: ${:,.2f}".format(minimum_price)
print "Maximum price: ${:,.2f}".format(maximum_price)
print "Mean price: ${:,.2f}".format(mean_price)
print "Median price ${:,.2f}".format(median_price)
print "Standard deviation of prices: ${:,.2f}".format(std_price)Statistics for Boston housing dataset:
Minimum price: $105,000.00
Maximum price: $1,024,800.00
Mean price: $454,342.94
Median price $438,900.00
Standard deviation of prices: $165,171.13
As a reminder, we are using three features from the Boston housing dataset: 'RM', 'LSTAT', and 'PTRATIO'. For each data point (neighborhood):
'RM'is the average number of rooms among homes in the neighborhood.'LSTAT'is the percentage of all Boston homeowners who have a greater net worth than homeowners in the neighborhood.'PTRATIO'is the ratio of students to teachers in primary and secondary schools in the neighborhood.
Using your intuition, for each of the three features above, do you think that an increase in the value of that feature would lead to anincrease in the value of 'MDEV' or adecrease in the value of 'MDEV'? Justify your answer for each.
Hint: Would you expect a home that has an 'RM' value of 6 be worth more or less than a home that has an 'RM' value of 7?
Answer:
For the RM feature:
-Intuition: An inrease in RM will increase MDEV
- A higher value for the avg. number of rooms in neighbouring houses could mean the house is in an area that generally has large houses. This can lead us to believe that there are generally fewer houses in the area, hence higher property value.
- This could be misleading for small towns since they too will have larger and fewer houses in a given area yet may still have (relatively) lower property values due to location.
For the LSTAT feature:
-Intuition: An inrease in LSTAT will decrease MDEV
- Being in an area that has a relatively lower net worth could mean lower property values. This may be an even stronger indicator if combined with the assumption for the
RMfeature above.
For the PTRATIO feature:
-Intuition: An inrease in PTRATIO will decrease MDEV
- A higher student-teacher ratio could mean that the area is more populated than the current infrastructure can handle. This will logically cause a drop in the house prices in that area.
- Another assumption could that lower student-teacher ratio means more private schools / specialized academies in the area which means a higher standard of education, hence a higher standard of living. All of which are things that leads us to believe an increase in
PRATIOcould mean a decrease inMDEV.
In this second section of the project, you will develop the tools and techniques necessary for a model to make a prediction. Being able to make accurate evaluations of each model's performance through the use of these tools and techniques helps to greatly reinforce the confidence in your predictions.
It is difficult to measure the quality of a given model without quantifying its performance over training and testing. This is typically done using some type of performance metric, whether it is through calculating some type of error, the goodness of fit, or some other useful measurement. For this project, you will be calculating the coefficient of determination, R2, to quantify your model's performance. The coefficient of determination for a model is a useful statistic in regression analysis, as it often describes how "good" that model is at making predictions.
The values for R2 range from 0 to 1, which captures the percentage of squared correlation between the predicted and actual values of thetarget variable. A model with an R2 of 0 always fails to predict the target variable, whereas a model with an R2 of 1 perfectly predicts the target variable. Any value between 0 and 1 indicates what percentage of the target variable, using this model, can be explained by thefeatures. A model can be given a negative R2 as well, which indicates that the model is no better than one that naively predicts the mean of the target variable.
For the performance_metric function in the code cell below, you will need to implement the following:
- Use
r2_scorefromsklearn.metricsto perform a performance calculation betweeny_trueandy_predict. - Assign the performance score to the
scorevariable.
from sklearn.metrics import r2_score
def performance_metric(y_true, y_predict):
""" Calculates and returns the performance score between
true and predicted values based on the metric chosen. """
score = r2_score(y_true, y_predict)
# Return the score
return scoreAssume that a dataset contains five data points and a model made the following predictions for the target variable:
| True Value | Prediction |
|---|---|
| 3.0 | 2.5 |
| -0.5 | 0.0 |
| 2.0 | 2.1 |
| 7.0 | 7.8 |
| 4.2 | 5.3 |
| Would you consider this model to have successfully captured the variation of the target variable? Why or why not? |
Run the code cell below to use the performance_metric function and calculate this model's coefficient of determination.
# Calculate the performance of this model
score = performance_metric([3, -0.5, 2, 7, 4.2], [2.5, 0.0, 2.1, 7.8, 5.3])
print "Model has a coefficient of determination, R^2, of {:.3f}.".format(score)Model has a coefficient of determination, R^2, of 0.923.
Answer:
Yes. By Inspecting the data, we can intuitively observe that values of predictions are generally close to the the true values. Also, when we run our R^2 tests, we get 0.923 which is considered a high accuracy value.
Your next implementation requires that you take the Boston housing dataset and split the data into training and testing subsets. Typically, the data is also shuffled into a random order when creating the training and testing subsets to remove any bias in the ordering of the dataset.
For the code cell below, you will need to implement the following:
- Use
train_test_splitfromsklearn.cross_validationto shuffle and split thefeaturesandpricesdata into training and testing sets.- Split the data into 80% training and 20% testing.
- Set the
random_statefortrain_test_splitto a value of your choice. This ensures results are consistent.
- Assign the train and testing splits to
X_train,X_test,y_train, andy_test.
# Import 'train_test_split'
from sklearn.cross_validation import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
features, prices, test_size=0.2, random_state=42)
# Success
print "Training and testing split was successful."Training and testing split was successful.
What is the benefit to splitting a dataset into some ratio of training and testing subsets for a learning algorithm?
Hint: What could go wrong with not having a way to test your model?
Answer:
We split the data into train and test partitions in order to get an honest evaluation of how our algorithims will perform with a data set it hasn't seen before (i.e. the closest possible to future data).
If we train and test on the same dataset, the liklihood that our algorithim will successfully deal with new real world data is relatively lower.
By doing this split, we can check to see if our algorithims are over fitting.
In this third section of the project, you'll take a look at several models' learning and testing performances on various subsets of training data. Additionally, you'll investigate one particular algorithm with an increasing 'max_depth' parameter on the full training set to observe how model complexity affects performance. Graphing your model's performance based on varying criteria can be beneficial in the analysis process, such as visualizing behavior that may not have been apparent from the results alone.
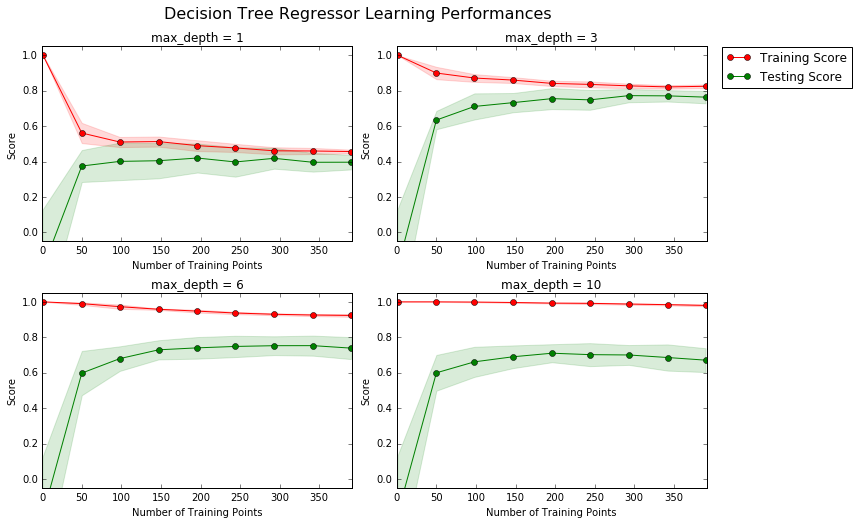
The following code cell produces four graphs for a decision tree model with different maximum depths. Each graph visualizes the learning curves of the model for both training and testing as the size of the training set is increased. Note that the shaded region of a learning curve denotes the uncertainty of that curve (measured as the standard deviation). The model is scored on both the training and testing sets using R2, the coefficient of determination.
Run the code cell below and use these graphs to answer the following question.
# Produce learning curves for varying training set sizes and maximum depths
vs.ModelLearning(features, prices)Choose one of the graphs above and state the maximum depth for the model. What happens to the score of the training curve as more training points are added? What about the testing curve? Would having more training points benefit the model?
Hint: Are the learning curves converging to particular scores?
Answer:
Graph #2 // max-depth = 3
The training curve starts with a score of 1, which is expected since our model has been built around it. It does however decline slighly during the initial training points since our model isn't overfitted (as compared to the max-depth = 10 where the training curve keeps a consistent score).
It's also expected to see that the training set improves greatly in the begining and reaches a limit of about 0.8 accuracy score. Other graphs that have a higher or lower max-depth value are displaying lower accuracy that both curves are converging to.
Having more data will not benefit the accuracy of the predictions since the score values are converging to 0.8. This is true for both training and testing datasets.
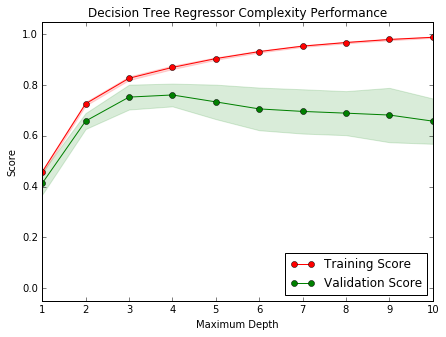
The following code cell produces a graph for a decision tree model that has been trained and validated on the training data using different maximum depths. The graph produces two complexity curves — one for training and one for validation. Similar to thelearning curves, the shaded regions of both the complexity curves denote the uncertainty in those curves, and the model is scored on both the training and validation sets using the performance_metric function.
Run the code cell below and use this graph to answer the following two questions.
vs.ModelComplexity(X_train, y_train)When the model is trained with a maximum depth of 1, does the model suffer from high bias or from high variance? How about when the model is trained with a maximum depth of 10? What visual cues in the graph justify your conclusions?
Hint: How do you know when a model is suffering from high bias or high variance?
Answer:
When a model is trained with max-depth of 1, we can say the model suffers from high bias since our Model Complexity is relatively lower. When the model is trained with a max-depth of 10, it suffers from high variance. As model complexity increases, bias decreases and variance increases.
We can observe this above if we look at the training and testing curves in the Complexity Performance graph. As we increase our maximum depth, the scores diverage or become more variable.
Which maximum depth do you think results in a model that best generalizes to unseen data? What intuition lead you to this answer?
Answer:
Graph #2 // max-depth = 3
When the maximum depth is 3, we minimize both variance and bias, hence it's the bence level of complexity for our model.
Choosing more than 3 leads us to high variance and going lower than 3 leads to lower scores and high bias.
In this final section of the project, you will construct a model and make a prediction on the client's feature set using an optimized model from fit_model.
What is the grid search technique and how it can be applied to optimize a learning algorithm?
Answer:
Grid search is a technique that allows us to run our algorithim with permutations of the important parameters, we can then choose the permutation that gives us the best fit.
For example, we discussed above how we may need to change the max-depth value and check which configuration gives us the lowest variance and bias. We achieve this programatically by using grid search to try out the different values of max-depth.
What is the k-fold cross-validation training technique? What benefit does this technique provide for grid search when optimizing a model?
Hint: Much like the reasoning behind having a testing set, what could go wrong with using grid search without a cross-validated set?
Answer:
K-fold cross-validation is a way of randomly partitioning the data into K equal samples. One of those segments is kept for testing and rest is used for training. This folding process is then repeated, each time while using a different partition for testing as shown in the figure below:
This technique is useful when we use it in combination with grid search since we can run each permutation of grid search with a different partition from the data, K.
The k results from the folds can then be averaged to produce a single estimation.
If we do grid search on a broken / bad dataset, the different permutations of our algorithim will return highly varying results compared to the average estimation.
Another great benefit of using k-fold with GridSearch to provide the best possible learning results and validation with a possibly limited data set.
Your final implementation requires that you bring everything together and train a model using thedecision tree algorithm. To ensure that you are producing an optimized model, you will train the model using the grid search technique to optimize the 'max_depth' parameter for the decision tree. The 'max_depth' parameter can be thought of as how many questions the decision tree algorithm is allowed to ask about the data before making a prediction. Decision trees are part of a class of algorithms called supervised learning algorithms.
For the fit_model function in the code cell below, you will need to implement the following:
- Use
DecisionTreeRegressorfromsklearn.treeto create a decision tree regressor object.- Assign this object to the
'regressor'variable.
- Assign this object to the
- Create a dictionary for
'max_depth'with the values from 1 to 10, and assign this to the'params'variable. - Use
make_scorerfromsklearn.metricsto create a scoring function object.- Pass the
performance_metricfunction as a parameter to the object. - Assign this scoring function to the
'scoring_fnc'variable.
- Pass the
- Use
GridSearchCVfromsklearn.grid_searchto create a grid search object.- Pass the variables
'regressor','params','scoring_fnc', and'cv_sets'as parameters to the object. - Assign the
GridSearchCVobject to the'grid'variable.
- Pass the variables
# Import 'make_scorer', 'DecisionTreeRegressor', and 'GridSearchCV'
from sklearn.tree import DecisionTreeRegressor
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import make_scorer
def fit_model(X, y):
""" Performs grid search over the 'max_depth' parameter for a
decision tree regressor trained on the input data [X, y]. """
# Create cross-validation sets from the training data
cv_sets = ShuffleSplit(X.shape[0], n_iter = 10, test_size = 0.20, random_state = 0)
# Create a decision tree regressor object
regressor = DecisionTreeRegressor(random_state=0)
# Create a dictionary for the parameter 'max_depth' with a range from 1 to 10
params = {'max_depth': range(1, 11)}
# Transform 'performance_metric' into a scoring function using 'make_scorer'
scoring_fnc = make_scorer(performance_metric)
# Create the grid search object
grid = GridSearchCV(regressor, params, scoring_fnc, cv=cv_sets)
# Fit the grid search object to the data to compute the optimal model
grid = grid.fit(X, y)
# Return the optimal model after fitting the data
return grid.best_estimator_Once a model has been trained on a given set of data, it can now be used to make predictions on new sets of input data. In the case of a decision tree regressor, the model has learned what the best questions to ask about the input data are, and can respond with a prediction for thetarget variable. You can use these predictions to gain information about data where the value of the target variable is unknown — such as data the model was not trained on.
What maximum depth does the optimal model have? How does this result compare to your guess inQuestion 6?
Run the code block below to fit the decision tree regressor to the training data and produce an optimal model.
# Fit the training data to the model using grid search
reg = fit_model(X_train, y_train)
# Produce the value for 'max_depth'
print "Parameter 'max_depth' is {} for the optimal model.".format(reg.get_params()['max_depth'])Parameter 'max_depth' is 4 for the optimal model.
Answer:
The max_depth value for the optimal model is 4.
This result aligns with my initial intuition from Question 6. The optimal model attempts to decrease variance and bias and to achieve this the model complexity can't be too low or too high.
Imagine that you were a real estate agent in the Boston area looking to use this model to help price homes owned by your clients that they wish to sell. You have collected the following information from three of your clients:
| Feature | Client 1 | Client 2 | Client 3 |
|---|---|---|---|
| Total number of rooms in home | 5 rooms | 4 rooms | 8 rooms |
| Household net worth (income) | Top 34th percent | Bottom 45th percent | Top 7th percent |
| Student-teacher ratio of nearby schools | 15-to-1 | 22-to-1 | 12-to-1 |
What price would you recommend each client sell his/her home at? Do these prices seem reasonable given the values for the respective features? Hint: Use the statistics you calculated in theData Exploration section to help justify your response.
Run the code block below to have your optimized model make predictions for each client's home.
# Produce a matrix for client data
client_data = [[5, 35, 15], # Client 1
[4, 55, 22], # Client 2
[8, 7, 12]] # Client 3
# Show predictions
for i, price in enumerate(reg.predict(client_data)):
print "Predicted selling price for Client {}'s home: ${:,.2f}".format(i+1, price)Predicted selling price for Client 1's home: $344,400.00
Predicted selling price for Client 2's home: $237,478.72
Predicted selling price for Client 3's home: $931,636.36
Answer:
The results predicted by the model are reasonable and along with initial hypothesis.
Let's consider Client 1, who has a predicted house price of $344,400.00 for 5 rooms. If we change Household Networth field to the 10th percentile from the 35th, the house price goes up to $486,584.48 (+0.85 standard devations), which also aligns initial assumptions.
A similar response happens when we increase the number of rooms to 7, the house price goes up to $ 577,500.00 (+1.4 standard devations).
The Student-teacher ratio however seems to have a smaller impact on the house prices, which we inspect by changes Client 1's ratio from 15:1 to 20:1 for the price to decrease. This is along the lines of our initial assumptions as well.
As a real-estate agent, and based purely on financial analysis, I'd recommend the following to my clients:
- Client 1 - Don't Sell
- Client 2 - Sell
- Client 3 - Sell
Earlier in this project, we explored the data and found out that the average house price in our dataset is $ 454,342.94. Also the average number of rooms for our dataset is ~6.4.
This means Client 1 and 2 both have houses below the average. For Client 1, I'd recommend that s/he keep the house because I believe its value will increase if the networth (currently 35th percentile) can increase. I would however advice clients 2 and 3 to sell because I don't think their values will change as time passes.
An optimal model is not necessarily a robust model. Sometimes, a model is either too complex or too simple to sufficiently generalize to new data. Sometimes, a model could use a learning algorithm that is not appropriate for the structure of the data given. Other times, the data itself could be too noisy or contain too few samples to allow a model to adequately capture the target variable — i.e., the model is underfitted. Run the code cell below to run the fit_model function ten times with different training and testing sets to see how the prediction for a specific client changes with the data it's trained on.
vs.PredictTrials(features, prices, fit_model, client_data)Trial 1: $332,850.00
Trial 2: $411,417.39
Trial 3: $346,500.00
Trial 4: $324,450.00
Trial 5: $413,334.78
Trial 6: $411,931.58
Trial 7: $344,750.00
Trial 8: $407,232.00
Trial 9: $306,000.00
Trial 10: $316,890.00
Range in prices: $107,334.78
In a few sentences, discuss whether the constructed model should or should not be used in a real-world setting.
Hint: Some questions to answering:
- How relevant today is data that was collected from 1978?
- Are the features present in the data sufficient to describe a home?
- Is the model robust enough to make consistent predictions?
- Would data collected in an urban city like Boston be applicable in a rural city?
Answer:
This model should not be used in a real-world setting for a few reasons:
-
Data collected almost 40 years ago would be irrelevant to today's prices as markets evolve and change, house prices and other factors such as currency value will also change.
-
The data provided on each home isn't sufficient to make accurate predictions in today's marketplace. For example, you could start taking into account features such as parks in the area or the number of universities in the city to better predict the price of a house.
-
The model makes predictions with a range of about 10% (compared to max price value) which isn't considered robust enough.
-
The model is trained with data from a certain city in a certain point in time, hence the model will likely underform with variable data from different types of cities (e.g. rural cities) as discussed in the answer to Question 1.