VecCore is a simple abstraction layer on top of other vectorization
libraries. It provides an architecture-independent API for
expressing vector operations on data. Code written with this API can then
be dispatched to one of several backends implemented using
libraries like Vc,
UME::SIMD, or a scalar implementation.
This allows one to get the best performance on platforms supported by Vc and
UME::SIMD without losing portability to unsupported architectures like PowerPC,
for example, where the scalar backends can be used instead without requiring
changes in user code. Another advantage is that, unlike with compiler intrinsics,
the same code can be compiled for SSE, AVX2, AVX512, etc, without modifications.
With the addition of new backends, such as the new backend based on C++20 and
std::experimental::simd, users can automatically take advantage of new
features and better performance. This backend supports AVX512 on Intel/AMD64 and
NEON on ARM/ARM64, with best performance in most cases. However, it does require
compiling code in C++20 mode, which may not always be possible, so there is
still an advantage in using it via VecCore's implementation to have a fallback
when C++20 is not avaialble.
The bench directory of the repository has several usage examples of the VecCore API that are used to compare how different backends perform in various circumstances. Below we show how to convert a scalar function to compute a Julia Set to work with SIMD instructions:
void julia(float xmin, float xmax, int nx, flaot ymin, float ymax, int ny,
int max_iter, unsigned char *image, float real, float im)
{
float dx = (xmax - xmin) / nx;
float dy = (ymax - ymin) / ny;
for (int i = 0; i < nx; ++i) {
for (int j = 0; j < ny; ++j) {
int k = 0;
float x = xmin + i * dx, cr = real, zr = x;
float y = ymin + j * dy, ci = im, zi = y;
do {
x = zr*zr - zi*zi + cr;
y = 2.0f * zr*zi + ci;
zr = x;
zi = y;
} while (++k < max_iter && (zr*zr + zi*zi < 4.0f));
image[ny*i + j] = k;
}
}
}template<typename T>
void julia_v(Scalar<T> xmin, Scalar<T> xmax, size_t nx, Scalar<T> ymin, Scalar<T> ymax, size_t ny,
Scalar<Index<T>> max_iter, unsigned char *image, Scalar<T> real, Scalar<T> im)
{
T iota(0.0);
for (size_t i = 0; i < VectorSize<T>(); ++i)
Set<T>(iota, i, i);
T dx = T(xmax - xmin) / T(nx);
T dy = T(ymax - ymin) / T(ny), dyv = iota * dy;
for (size_t i = 0; i < nx; ++i) {
for (size_t j = 0; j < ny; j += VectorSize<T>()) {
Scalar<Index<T>> k(0);
T x = xmin + T(i) * dx, cr = real, zr = x;
T y = ymin + T(j) * dy + dyv, ci = im, zi = y;
Index<T> kv(0);
Mask<T> m(true);
do {
x = zr*zr - zi*zi + cr;
y = T(2.0) * zr*zi + ci;
MaskedAssign<T>(zr, m, x);
MaskedAssign<T>(zi, m, y);
MaskedAssign<Index<T>>(kv, m, ++k);
m = zr*zr + zi*zi < T(4.0);
} while (k < max_iter && !MaskEmpty(m));
for (size_t k = 0; k < VectorSize<T>(); ++k)
image[ny*i + j + k] = (unsigned char) Get(kv, k);
}
}
}The differences appear where branching is required and masks need to be used instead of simple conditionals. In some places, casting scalars to the correct type is also necessary in order enable their promotion to the correct SIMD vector type.
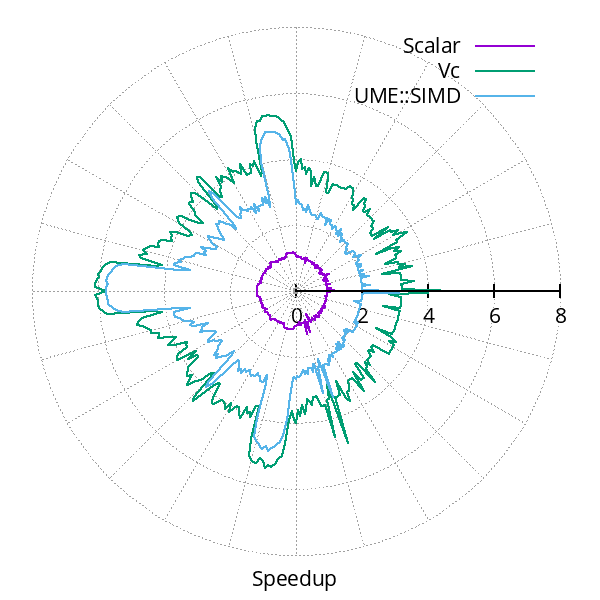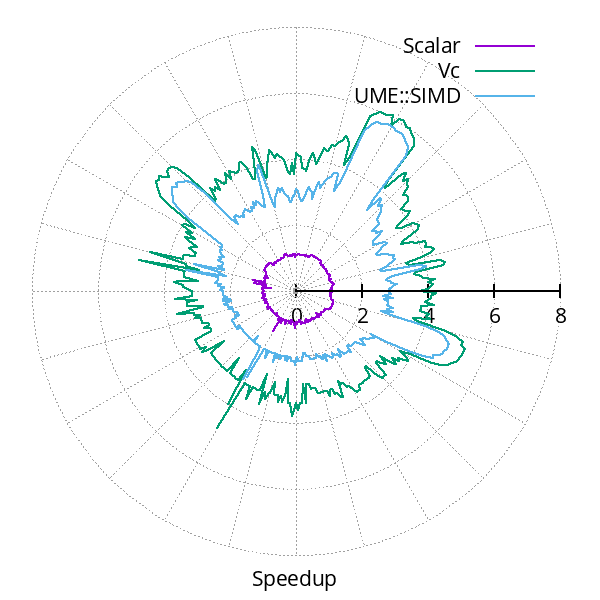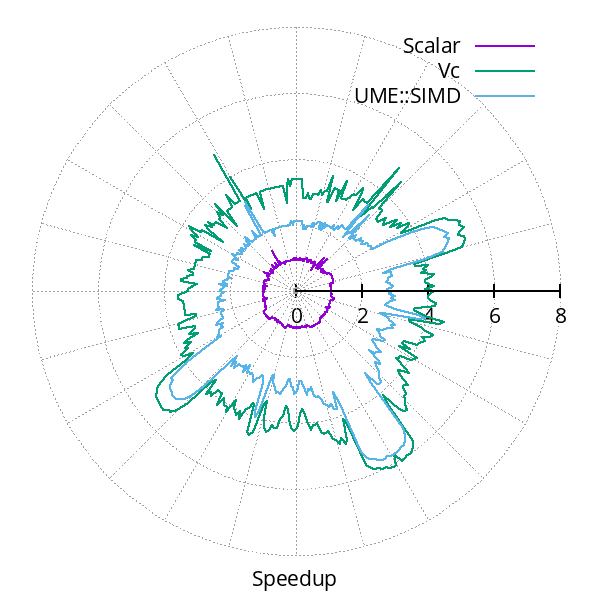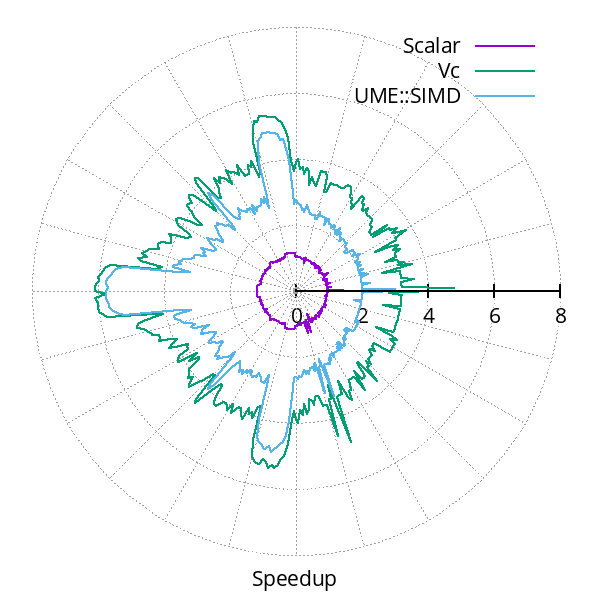
Gains in performance usually depend not only on the code being vectorized, but also on the runtime characteristics of the actual computations. For example, when computing Julia sets, it matters what structure it has, as that determines how much coherence there is between nearby pixels. That is, the more iterations that get computed in vector mode for nearby pixels, the more performance is improved. On the other hand, when more iterations are performed with elements masked out, speedup is lower. Therefore, the fractal with the largest interior consisting of diverging points (shown in black) has the largest speedup. The figure below illustrates this fact for different fractals (left) by showing the speedup as the point where the lines cross the axis of the radial plot (right).
VecCore supports Linux, Mac OS X, and Windows. To compile software using VecCore, you will need a compiler with support for C++11. We recommend using at least the following compiler versions:
- GCC 6.5.0
- Clang 9.0
- AppleClang 11.0
- Intel® C/C++ Compiler 19.1
- Microsoft Visual Studio 17 2019
Additionally, you will need CMake 3.9 or later, and you may want to install a SIMD library such as
- Vc (version 1.4 or later)
- UME::SIMD (version 0.8.1 or later)
- std::experimental::simd (included in libstdc++ from GCC 11 or later)
and/or
- Nvidia's CUDA SDK (version 10.2 or later).
The documentation can be generated by Doxygen by enabling -DBUILD_DOCS=True
when configuring, then building the doxygen target with make doxygen. It is
also available online at https://root-project.github.io/veccore.
A list of publications is available here.