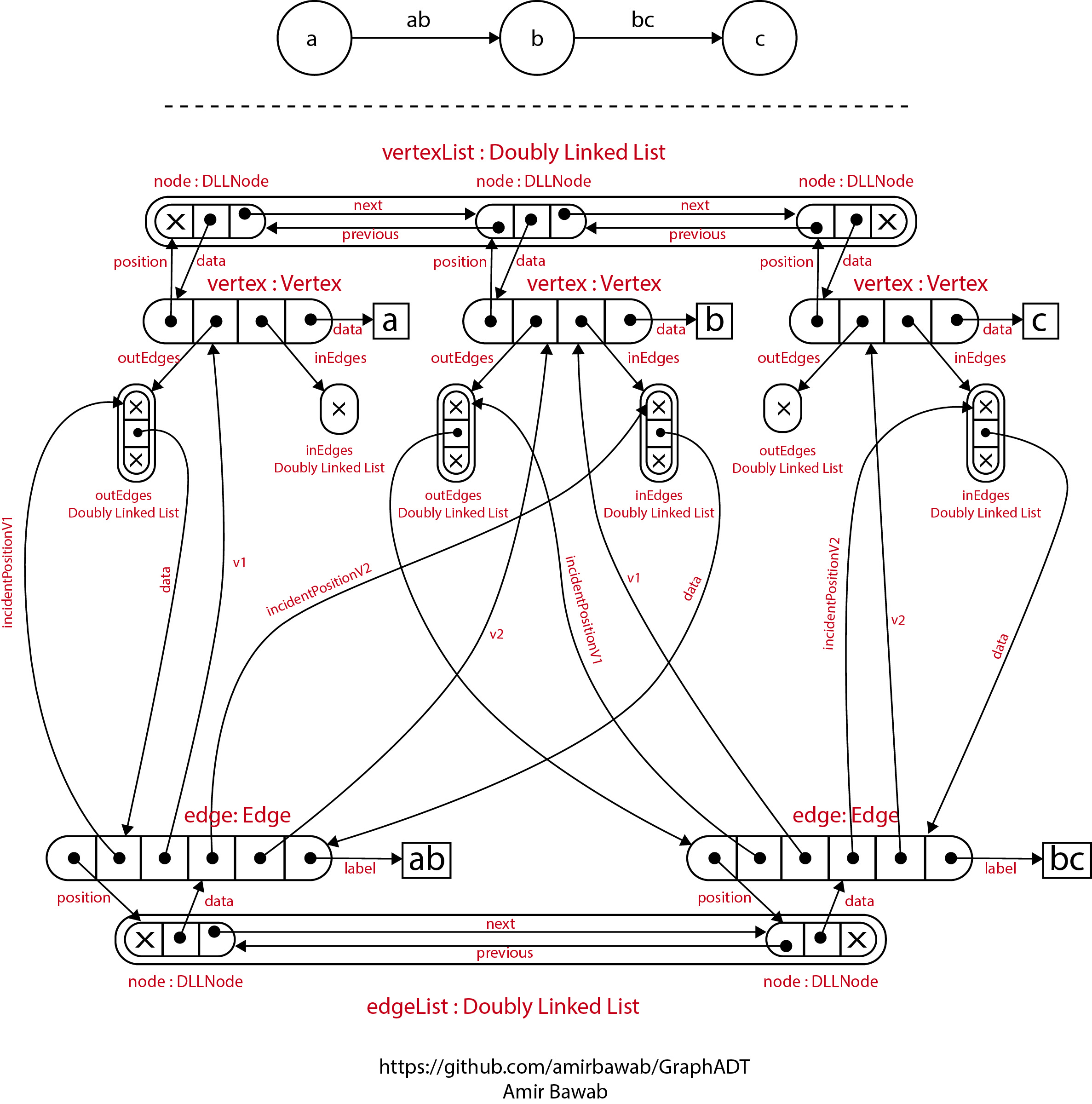
####What's New:
- Bug in cloning fixed
- Structure modified
- Only useful methods are accessible for each class
- Edges now support a label of any type
####Methods to build your graph
#####Graph methods and complexities:
| Method | Return | Explanation | Complexity |
|---|---|---|---|
| addEdge(...) | Array of the added edges | Add one edge between two vertices. Add another edge in the opposite direction if the graph is undirected | O(1) |
| addVertex(data) | Vertex added | Add a vertix to the graph | O(1) |
| areAdjacent(v1,v2) | Boolean | Checks if two vertices are adjacent | O(min(v1 deg, v2 deg)) |
| BFS() | Array of vertices traversed by BFS | Traverse the graph with Breadth First Search | O(|V| + |E|) |
| BFS(vertex) | Array of vertices traversed by BFS | Traverse reachable vertices in a graph with Breadth First Search starting from a specific vertex | O(|V| + |E|) |
| DFS() | Array of vertices traversed by DFS | Traverse the graph with Depth First Search | O(|V| + |E|) |
| DFS(vertex) | Array of vertices traversed by DFS | Traverse reachable vertices in a graph with Depth First Search starting from a specific vertex | O(|V| + |E|) |
| connectedComponents() | Number of connected components | Checks how many connected components the graph contains | O(|V| + |E|) |
| isConnected() | Boolean | Checks if the graph is connected | O(|V| + |E|) |
| isCyclic() | Boolean | Checks if the graph is cyclic | O(|V| + |E|) |
| isDirected() | Boolean | Checks if the graph is directed | O(1) |
| clone() | Graph | Clone graph vertices and edges without cloning the data contained by the vertices | O(|V| + |E|) |
| dijkstra(v) | void | Trace the shortest path from v to all other vertices | O(|V|log|V|+ |E|) |
| dijkstra(v1,v2) | Array of edges | Trace the shortest path from v1 to v2 | O(|V|log|V|+ |E|) |
| removeEdge(e) | void | Removes an edge from the graph | O(1) |
| removeVertex(v) | void | Removes a vertex from the graph | O(v deg) |
| transitiveClosure() | void | Apply Floyd–Warshall algorithm for Transitive closure. If i -> k and k -> j then i -> j if i & j are not already connected | O(|V|3) |
| edges() | NodeIterator | Gives an iterator on the list of edges | O(1) |
| vertices() | NodeIterator | Gives an iterator on the list of vertices | O(1) |
| edges_array() | Array of edges | Gives an array of all the graph edges | O(|E|) |
| vertices_array() | Array of vertices | Gives an array of all the graph vertices | O(|V|) |
####Populate your graph
#####A) Use an input file:
######Input 1 : MIT.TXT
size=5
0 = A
1 = B
2 = C
3 = D
4 = E
;
(0,1,10)
(0,2,3)
(1,3,2)
(1,2,1)
(2,1,4)
(2,3,8)
(2,4,2)
(3,4,7)
(4,3,9)
;
Understand input file
First line is the number of vertices:
size = X where X is the number of vertices
The next X lines will contain the vertices ID and NAME:
ID = NAME where ID is unique for each vertex and start from 0 up to X-1. NAME is any string (no quotes are required).
; is used to mark the end of vertex declaration and initialization
The next lines are the edges between vertices (Optional: edges weight and label)
(FROM, TO , WEIGHT) = LABEL where FROM & TO belong to ID. WEIGHT is a double value. LABEL is any string.
Alternative syntax:
Without LABEL: (FROM, TO, WEIGHT)
Without WEIGHT: (FROM, TO) = LABEL
Without WEIGHT & LABEL: (FROM, TO)
; is used to mark the end of edges declaration
Note:
- White spaces in the above syntax are ignored.
- Use
//or#at the beginning of a line to comment and ignore this line in the input file. - Graph read from an input file must be assigned to a graph variable of generic type
String.
Output of the graph driver on input 1: MIT.TXT:
Print graph state
Vertices:
<A> <B> <C> <D> <E>
Edges:
(<A>, <B>)
(<A>, <C>)
(<B>, <D>)
(<B>, <C>)
(<C>, <B>)
(<C>, <D>)
(<C>, <E>)
(<D>, <E>)
(<E>, <D>)
BFS:
<A> <B> <C> <D> <E>
DFS
<A> <B> <D> <E> <C>
Is connected: true
Is directed: true
Is cyclic: true
Number of Connected components: 1
Clone graph ...
Apply Transitive closure to the cloned graph
Print state of the new graph
Vertices:
<A> <B> <C> <D> <E>
Edges:
(<A>, <B>)
(<A>, <C>)
(<B>, <D>)
(<B>, <C>)
(<C>, <B>)
(<C>, <D>)
(<C>, <E>)
(<D>, <E>)
(<E>, <D>)
(<A>, <D>)
(<A>, <E>)
(<B>, <E>)
#####B) Use methods:
public static void main(String[] args) {
Graph<String,String> graph = new Graph<String,String>(false); // Undirected graph
Vertex<String,String> v1 = graph.addVertex("A");
Vertex<String,String> v2 = graph.addVertex("B");
Edge<String,String> e1[] = graph.addEdge(v1, v2);
System.out.println(graph);
}Output of the above code:
Vertices:
<A> <B>
Edges:
(<A>, <B>)
(<B>, <A>)
Note:
Graph <E,T>.Eis the vertex generic type.Tis the edge generic type.- This method (B) is more dynamic compared to the first method (A) because it allows you to choose any generic type for your graph vertices data and edges label. For instance, you can create a class
Personand build a graph with vertices data of typePersonand edges label of typeInteger, so that every edge between two persons is a relationship and the edge label is the type of this relationship (1: friends, 2: family, etc... ).
###Example of a project using the GraphADT: Montreal metro
#####Input file: Metro.TXT (Available in this repo)
#####Write a program to find the shortest path from Côte-Vertu to Jean-Drapeau
######Code:
try {
Graph<String,String> graph = Graph.inParser("Metro.txt", false);
Vertex<String,String> v[] = graph.vertices_array();
for(Edge<String,String> e : graph.dijkstra(v[14], v[30]))
System.out.println(e);
System.out.println("-------------------------------");
System.out.println(String.format("Total distance: %.2f meters", v[30].getDijkstra_value()));
} catch (FileNotFoundException e) {
e.printStackTrace();
}#####Output:
(<Côte-Vertu>, <Du Collège>)
(<Du Collège>, <De La Savane>)
(<De La Savane>, <Namur>)
(<Namur>, <Plamondon>)
(<Plamondon>, <Côte-Sainte-Catherine>)
(<Côte-Sainte-Catherine>, <Snowdon>)
(<Snowdon>, <Villa-Maria>)
(<Villa-Maria>, <Vendôme>)
(<Vendôme>, <Place-Saint-Henri>)
(<Place-Saint-Henri>, <Lionel-Groulx>)
(<Lionel-Groulx>, <Georges-Vanier>)
(<Georges-Vanier>, <Lucien-L'Allier>)
(<Lucien-L'Allier>, <Bonaventure>)
(<Bonaventure>, <Square-Victoria-OACI>)
(<Square-Victoria-OACI>, <Place-d'Armes>)
(<Place-d'Armes>, <Champ-de-Mars>)
(<Champ-de-Mars>, <Berri-UQAM>)
(<Berri-UQAM>, <Jean-Drapeau>)
-------------------------------
Total distance: 15173.61 meters
#####References:
Wikipedia
MIT Introduction to algorithms