This repository contains a small C++ header file that implements the Jacobi eigenvalue algorithm. It is free of copyright.
The Jacobi algorithm remains one of the oldest and most popular methods for diagonalizing dense, square, real, symmetric matrices.
The matrices themselves can be implemented as X** (pointer-to-pointer), vector<vector<X>>&, fixed-size arrays, or any other C or C++ object which supports [i][j] indexing. (Here X is any real numeric type. Complex numbers are not supported.)
(Memory allocation on the heap is avoided except during instantiation.)
The main feature of this repository is it's license.
As of late 2020, no simple public domain C++11 code yet exists for matrix diagonalization. Other C++ libraries such as Eigen or GSL are typically much larger and use more restrictive licenses. (On several occasions, this has prevented me from including their code in other open-source projects with incompatible licenses.) Some repositories may unwittingly contain code snippets from other sources, such as numerical recipes. This short repository was written from scratch. No lines of code were borrowed or adapted from other sources.
Caveats: The code in this repository does not run in parallel, and only works on dense square real symmetric matrices. However it is reasonably short, simple, fast and reliable. You can do anything you like with this code.
#include "jacobi_pd.hpp"
using namespace jacobi_pd;
// ...
int n = 3; // Matrix size
double **M; // A symmetric n x n matrix you want to diagonalize
double *evals; // Store the eigenvalues here.
double **evecs; // Store the eigenvectors here.
// Allocate space for M, evals, and evecs (omitted)...
M[0][0] = 2.0; M[0][1] = 1.0; M[0][2] = 1.0;
M[1][0] = 1.0; M[1][1] = 2.0; M[1][2] =-1.0; //Note: The matrix
M[2][0] = 1.0; M[2][1] =-1.0; M[2][2] = 2.0; //must be symmetric.
// Now create an instance of Jacobi ("eigen_calc").
Jacobi<double, double*, double**> eigen_calc(n);
// Note:
// If the matrix you plan to diagonalize (M) is read-only, use this instead:
// Jacobi<double, double*, double**, double const*const*> eigen_calc(n);
// If you prefer using C++ vectors over C-style pointers, this works also:
// Jacobi<double, vector<double>&, vector<vector<double>>&,
// const vector<vector<Scalar>>&> eigen_calc(n);
// Now, calculate the eigenvalues and eigenvectors of M
eigen_calc.Diagonalize(M, evals, evecs); //(successful if return value is > 0)
// If you have many matrices to diagonalize, you can re-use "eigen_calc". (This
// is more efficient than creating a new "Jacobi" class instance for each use.)
std::cout << "eigenvalues: ";
for (int i=0; i < n; i++)
cout << evals[i] << " ";
cout << endl;
for (int i=0; i < n; i++) {
cout << "eigenvector" <<i+1<< ": ";
for (int j=0; j < n; j++)
cout << evecs[i][j] << " ";
cout << endl;
}Copy the file(s) in the include subdirectory, to a location in your include path. No linking is necessary. This is a header-only library.
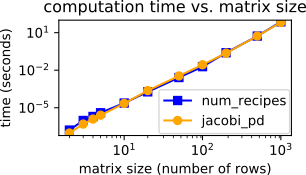
jacobi_pd has been tested for accuracy and memory safety over a wide range of array types, matrix sizes, eigenvalue magnitudes and degeneracies. jacobi_pd code is currently used in the popular LAMMPS and colvars MD simulation tools.
A C++11 compatible compiler.
jacobi_pd is available under the terms of the Creative-Commons-Zero license.
Please send me corrections or suggestions.