comp9417-machine-learning-and-data-mining

comp9417 machine learning and data mining notes and work

Week 1: Regression

1.1 Supervised Learning

How to predict the house price given by its size?

Collect statistics -> Each house's preice and its size, then we have a table:
Find the relationship between these two variables, which means we need to find a function y = f(x) according to the table.

How do we know how good the function is? Cost function or MSE(mean squared error) to calculate the error(difference between predicted value and true value)

This is how Supervised Learning works:

1.2 Univariate Linear Regression

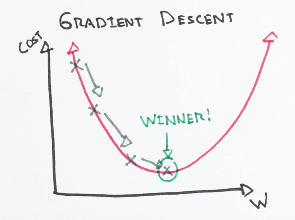
The core idea is to obtain a line that best fits the data. The best fit line is the one for which total prediction error (MSE) are as small as possible. Error is the distance between the point to the regression line.

Eg: Predict 'house price' given the 'size of the house', y = f(x) = b₁x + b₀(y=value of house, x=size of house).

What we need to find is b₀ and b₁.

Coefficient Formula:

1.3 Multivariate Linear Regression

Week 2 Classification

2.1 Lazy Learners

Lazy learners simply store the training data and wait until a testing data appear. When it does, classification is conducted based on the most related data in the stored training data. Compared to eager learners, lazy learners have less training time but more time in predicting.

Ex. k-nearest neighbor, Case-based reasoning

2.2 Eager Learners

Eager learners construct a classification model based on the given training data before receiving data for classification. It must be able to commit to a single hypothesis that covers the entire instance space. Due to the model construction, eager learners take a long time for train and less time to predict.

Ex. Decision Tree, Naive Bayes, Artificial Neural Networks

2.3 K-nearest neighbor

In k-NN classification, the output is a class membership. An object is classified by a plurality vote of its neighbors, with the object being assigned to the class most common among its k nearest neighbors (k is a positive integer, typically small). If k = 1, then the object is simply assigned to the class of that single nearest neighbor

Thus, we need to find a formula to measure the distance.

Minkowski Distance:

The 2-norm refers to Euclidean Distance, and the 1-norm refers to Manhattan Distance. If p is infinitely large, distance is called Chebyshev distance.

2.4 Bayesian

h_MAP = arg max(P(h|D))

Learning a real valued function: maximum likelihood hypothesis h_ML is the one that minimises the sum of squared error.

multivariate Bernoulli distribution: For the i-th word in our vocabulary we have a random variable Xi governed by a Bernoulli distribution. The joint distribution over the bit vector X = (X1, . . . , Xk) is called a multivariate Bernoulli distribution.

multinomial distribution: Every word position in an e-mail corresponds to a categorical variable with k outcomes, where k is the size of the vocabulary. The multinomial distribution manifests itself as a count vector

2.5 Naive Bayes Classifier

D = (x, c) = <(x₁, x₂,...)(features), c(class)>, Learn P(C|X)

Continuous: Gaussian NB

Discrete: Multinomial or Multivariate

Deep Learning

3.1 Perceptron algorithm

3.2 Gradient Descent

Kernel

1. Duality

Linearly separable data. Dual view of Perceptron + SVM Dual Perceptron learning:

2. Kernel Trick

How to deal with non-separable data

solve: minimize |w| subject to (by Lagrange multiplier)

k(x1, x2) = (1+x1·x2)²

Ensemble

1. Bagging

Data1 ---> Model1 ----> Prediction1 (weak)
Data2 ---> Model2 ----> Prediction2 (weak)
...
Data_T----> Model_T --->prediction (weak)

Vote ---> Prediction

2. Random Forest

Data(sample data & sample feature)

3. Boosting(Adaptive Boost)

weak ----> strong

Form a large set of simple features
Initialize weights for training images

For T rounds
Normalize the weights
For available features from the set, train a classifier using a single feature and evaluate the training error
Choose the classifier with the lowest error
Update the weights of the training images: increase if classified wrongly by this classifier, decrease if correctly
Form the final strong classifier as the linear combination of the T classifiers (coefficient larger if training error is small)

c0 = 0
w1i = 1/N
for m=1...M:
3.choose weak learner km that minimize error
alpham = (1/2)log((1-e)/e)
calculate zm = zmsqrt(em(1-em))
w(i)(m+1) = w(i)(m)/z(m)
C= C(m-1)+alpham*Cm

unsupervised learning

K-mass clusters:

Assume k = 3
1.init clusters center randomly
2.Assign points X to clusters
3.recompute cluster's center
4.repeat 2, 3 until cluster centers don't change

Learning Theorem

X = set of instances (Space where data)
H = Hypothesis Set (Space of linear models...)
C = set of possible target outputs (C generates y's not predicted y)
D = Training instances generated by distribution D
D = {<x(i), c(x(i))>} i = 1...n

Training Error: # times that h(x) != c(x)
True Error: P(h(x) != c(x)) x from p (similar to test error)

Goal: try to know true error from training error

Consistency of h: h is consist with D, c iff h(x)=c(x) for all x belong to D. (zero training error)

Version Space: VShd = { h belong to H | Consistent (h, D)}

Find-S:

Init h to be most specific (most strict) h belong to H
For each x in D with c(x) == 1:
3.For each ai in h:
4. If a not satisfied, replace ai in h by next general constraint.
return h

*Candidate Elimination: start from the most specific and general hypothesis simultaneously.

Tool2:epsilon-Exhausting VS(h,d) --> every h belong to VS(hd) has true error < epsilon
Theorem: if |H| < infinity, D = {<xi, c(xi)>}(i=1..M) with examples drawn from P, then epsilon = [0, 1]. Probability that VS(hd) is not epsilon-exhaused is less or equal to |H|e^(-ep*M)

VC dimension complexity of H: Dichotomy of Set S is partition of S into 2 distinct subset.
Shattering a set of instances S = {} by H if for every dichotomy of S there is h consistent.

anantkm/comp9417-machine-learning-and-data-mining