Bayesian Physics Informed Neural Networks for Data Assimilation and Spatio-Temporal Modelling of Wildfires
This code implements the Bayesian Physics Informed Neural Network (PINN) for modelling a wildfire fire-front as it progresses over space and time as described in the following paper:
Joel Janek Dabrowski, Daniel Edward Pagendam, James Hilton, Conrad Sanderson, Daniel MacKinlay, Carolyn Huston, Andrew Bolt, Petra Kuhnert, "Bayesian Physics Informed Neural Networks for Data Assimilation and Spatio-Temporal Modelling of Wildfires", Spatial Statistics, Volume 55, June 2023, 100746
Links:
Published: https://www.sciencedirect.com/science/article/pii/S2211675323000210
Preprint: https://arxiv.org/abs/2212.00970
BibTex citation:
@article{DABROWSKI2023100746,
title = {Bayesian Physics Informed Neural Networks for data assimilation and spatio-temporal modelling of wildfires},
journal = {Spatial Statistics},
volume = {55},
pages = {100746},
year = {2023},
issn = {2211-6753},
doi = {https://doi.org/10.1016/j.spasta.2023.100746},
url = {https://www.sciencedirect.com/science/article/pii/S2211675323000210},
author = {Joel Janek Dabrowski and Daniel Edward Pagendam and James Hilton and Conrad Sanderson and Daniel MacKinlay and Carolyn Huston and Andrew Bolt and Petra Kuhnert},
keywords = {PINN, B-PINN, Level-set method, Uncertainty quantification, Neural network, Variational inference},
abstract = {We apply the Physics Informed Neural Network (PINN) to the problem of wildfire fire-front modelling. We use the PINN to solve the level-set equation, which is a partial differential equation that models a fire-front through the zero-level-set of a level-set function. The result is a PINN that simulates a fire-front as it propagates through the spatio-temporal domain. We show that popular optimisation cost functions used in the literature can result in PINNs that fail to maintain temporal continuity in modelled fire-fronts when there are extreme changes in exogenous forcing variables such as wind direction. We thus propose novel additions to the optimisation cost function that improves temporal continuity under these extreme changes. Furthermore, we develop an approach to perform data assimilation within the PINN such that the PINN predictions are drawn towards observations of the fire-front. Finally, we incorporate our novel approaches into a Bayesian PINN (B-PINN) to provide uncertainty quantification in the fire-front predictions. This is significant as the standard solver, the level-set method, does not naturally offer the capability for data assimilation and uncertainty quantification. Our results show that, with our novel approaches, the B-PINN can produce accurate predictions with high quality uncertainty quantification on real-world data.}
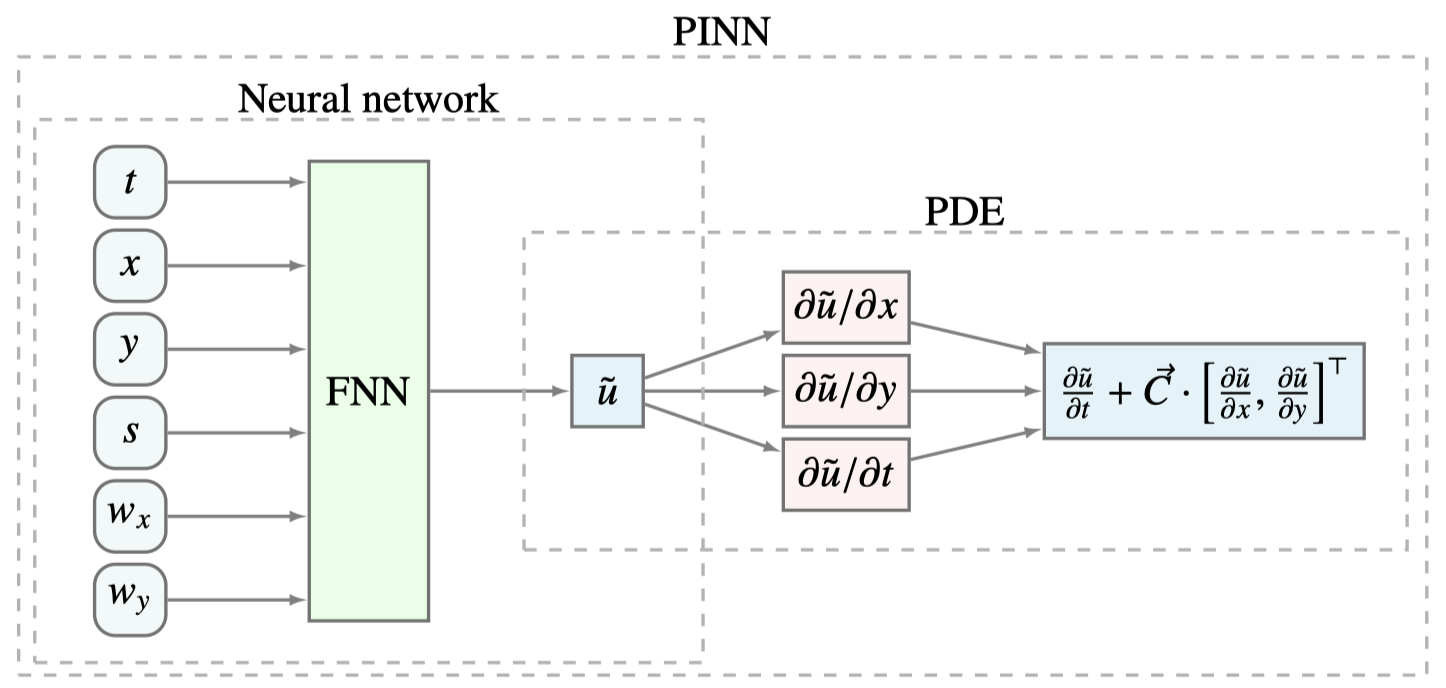
}The PINN architecture is illustrated in the following figure
The model inputs include the time t, the spatial location (x,y), the
fire-front speed c, and the wind speed w_x and w_y in the x- and
y-directions respectively. The Bayesian Feed Forward Neural Network (FNN)
outputs the level set function u where the zero level set of u describes the
predicted position of the fire-front. The partial derivatives of u with
respect to space and time are computed using automatic differentiation. These
partial derivatives are used to formulate the level set equation, which is used
as the part of the PINN's cost function. The loss function is represented in the
form of a posterior distribution which is approximated using variational
inference.
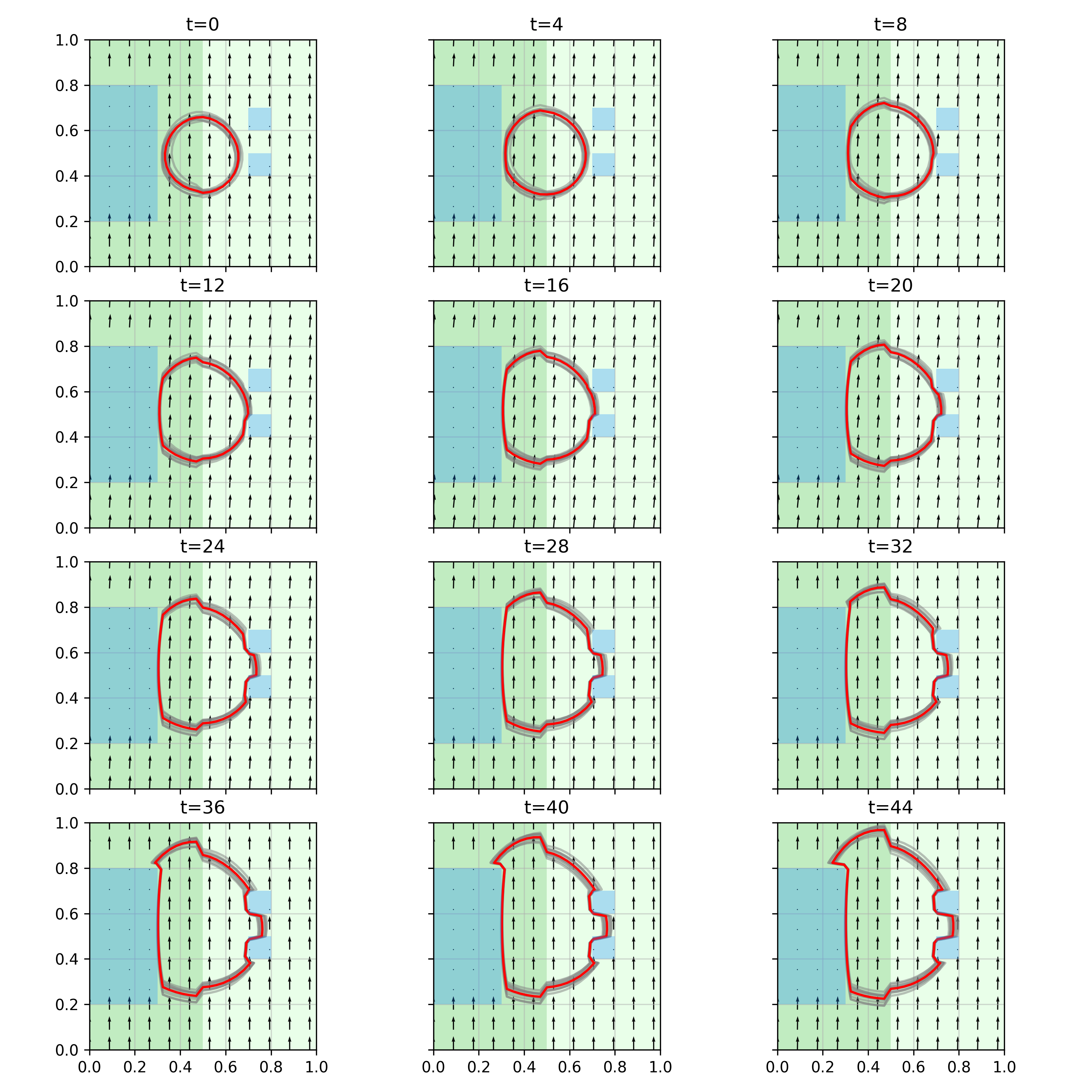
In this code, the results for the complex shape synthetic dataset are reproduced from the paper. The synthetic dataset described in section 4.1.2 of the paper and the results described in section 4.1.5 and figure 6 in the paper. The synthetic dataset describes a space comprising three obstacles that the fire-front can not propagate over, a time varying wind speed which follows a random walk in the positive y-direction, and a fire-front speed which is higher in the left half of the space than the right half.
The fire-front predicted by the trained model is illustrated in the below figure
The blue regions indicate the obstructions (e.g., water); the green regions indicate burnable land with the darker green having a higher fire-front speed properties than the lighter green region; the red isochrone plots the mean value of the prediction from the Bayesian PINN; and the grey isochrones plot samples from the Bayesian PINN.
Please see the paper for further details.
The file contents of this code repository are as follows:
| File | Description |
|---|---|
main.py |
The main file to train the PINN and reproduce the results from the paper. |
dataset.py |
Functions and utilities for generating the level set function and dataset samples. |
pinn.py |
Defines the PINN model. |
mlp.py |
Defines the Bayesian Feed Forward Neural Network (FNN). |
The main.py can be used to reproduce the results such as those illustrated in
the above figure. In lines 30-34, the training parameters may be set and these
parameters are described in the following table:
| Parameter | Description |
|---|---|
train_model |
If set to True, the model is trained, otherwise the model is only evaluated and plots are produced. Note the model must be trained at least once to produce the model parameters that are required for evaluation (see save_file below). |
n_epochs |
Number of epochs to train over. This is currently set to 16000. |
learning_rate |
Learning rate used for the ADAM optimiser. This is currently set to 1e-3 |
predictive_cost |
If set to True, the Forecast Likelihood described in the paper is used. |
save_file |
The path to the file in which the PINN model parameters are stored. |
This code is run on Python version 3.10.9. This code and the required Python
packages can be installed using the following:
git clone https://github.com/jjdabr/BPINN-Wildfire.git
pip install -r requirements.txt