Implementation of the 2D self-organizing map, with support for NumPy arrays and Pandas DataFrames. Most features were implemented using NumPy, with Scikit-learn for standardization and PCA operations.
- Stepwise and batch training
- Random weight initialization
- Random sampling weight initialization
- Linear weight initialization (with PCA)
- Automatic selection of map size ratio (with PCA)
- Support for cyclic arrays, for toroidal or spherical maps
- Gaussian and Bubble neighborhood functions
- Support for custom decay functions
- Support for visualization (U-matrix, activation matrix)
- Support for supervised learning (label map)
- Support for NumPy arrays, Pandas DataFrames and regular lists of values
In the following code excerpt (also available in test.py) is an example of instantiation and training of a SOM with the Iris dataset:
# Import python_som
import python_som
# Import NumPy and Pandas for storing data
import numpy as np
import pandas as pd
# Import libraries for plotting results
import matplotlib.pyplot as plt
import seaborn as sns
# Load Iris dataset and columns of features and labels
iris = sns.load_dataset('iris')
target = iris.iloc[:, -1].to_numpy()
iris = iris.iloc[:, :-1].to_numpy()
# Transform labels into numeric codes for plotting
tg = np.zeros(len(target), dtype=int)
tg[target == 'setosa'] = 0
tg[target == 'versicolor'] = 1
tg[target == 'virginica'] = 2
# Instantiate SOM from python_som
# Selecting shape automatically (providing dataset for constructor)
# Using default decay and distance functions
# Using gaussian neighborhood function
# Using cyclic arrays in the vertical and horizontal directions
som = python_som.SOM(x=20, y=None, input_len=iris.shape[1], learning_rate=0.5, neighborhood_radius=1.0,
neighborhood_function='gaussian', cyclic_x=True, cyclic_y=True, data=iris)
# Initialize weights of the SOM with linear initialization
som.weight_initialization(mode='linear', data=iris)
# Training SOM with default number of iterations
# Using batch learning process
som.train(data=iris, n_iteration=len(iris), mode='batch', verbose=True)
# Calculating distance matrix for plotting
umatrix = som.distance_matrix().T
# Plotting U-matrix with seaborn/matplotlib
plt.figure(figsize=som.get_shape())
plt.pcolor(umatrix, cmap='bone_r')
markers = ['o', 's', 'D']
colors = ['C0', 'C1', 'C2']
for cnt, xx in enumerate(iris):
w = som.winner(xx) # getting the winner
plt.plot(w[0] + .5, w[1] + .5, markers[tg[cnt]], markerfacecolor='None',
markeredgecolor=colors[tg[cnt]], markersize=12, markeredgewidth=2)
plt.axis([0, som.get_shape()[0], 0, som.get_shape()[1]])
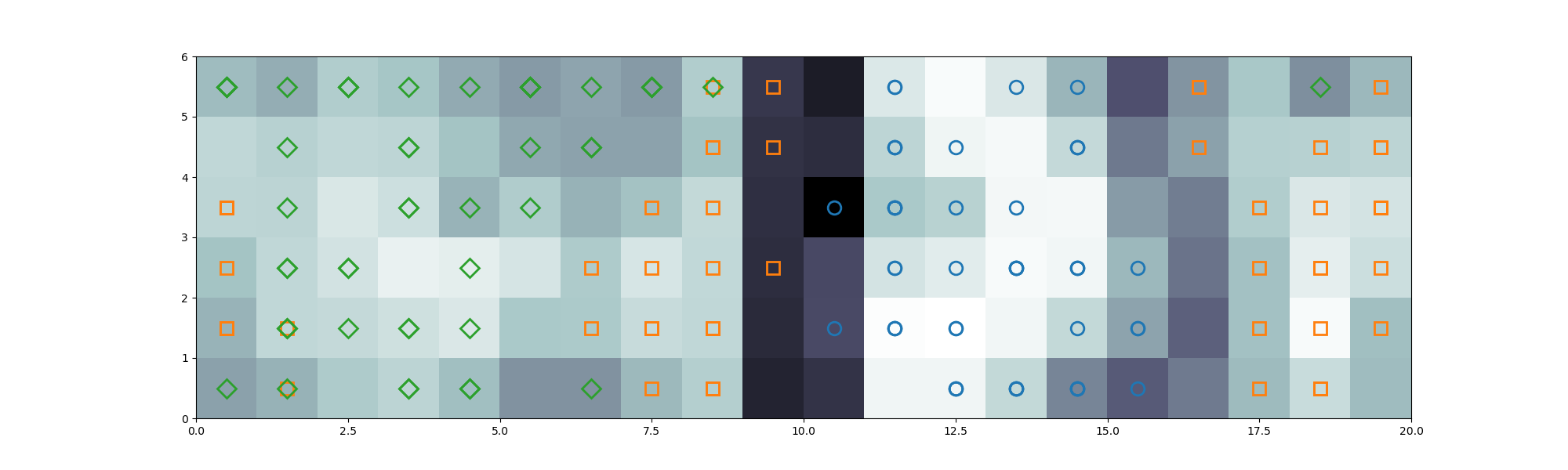
plt.show()The following image is generated from the previous test code, with the U-matrix of the trained SOM, and the distribution of the instances from the Iris dataset. In this graph, the instances are mapped to the self-organizing map, with color codes for each different label:
- Setosa: blue circle
- Versicolor: orange square
- Virginica: green diamond
The following are lists of public methods and functions currently available in the SOM class. The full documentation of each method can be found in the source code:
- _asymptotic_decay
- _linear_decay
- _exponential_decay
- _inverse_decay
- _euclidean_distance
- SOM
- SOM.get_shape
- SOM.get_weights
- SOM.set_learning_rate
- SOM.set_neighborhood_radius
- SOM.activate
- SOM.winner
- SOM.quantization
- SOM.quantization_error
- SOM.distance_matrix
- SOM.activation_matrix
- SOM.winner_map
- SOM.label_map
- SOM.train
- SOM.weight_initialization
This implemetation was based on the following paper, by Professor Teuvo Kohonen:
Teuvo Kohonen, Essentials of the self-organizing map, Neural Networks, Volume 37, 2013, Pages 52-65, ISSN 0893-6080, https://doi.org/10.1016/j.neunet.2012.09.018.