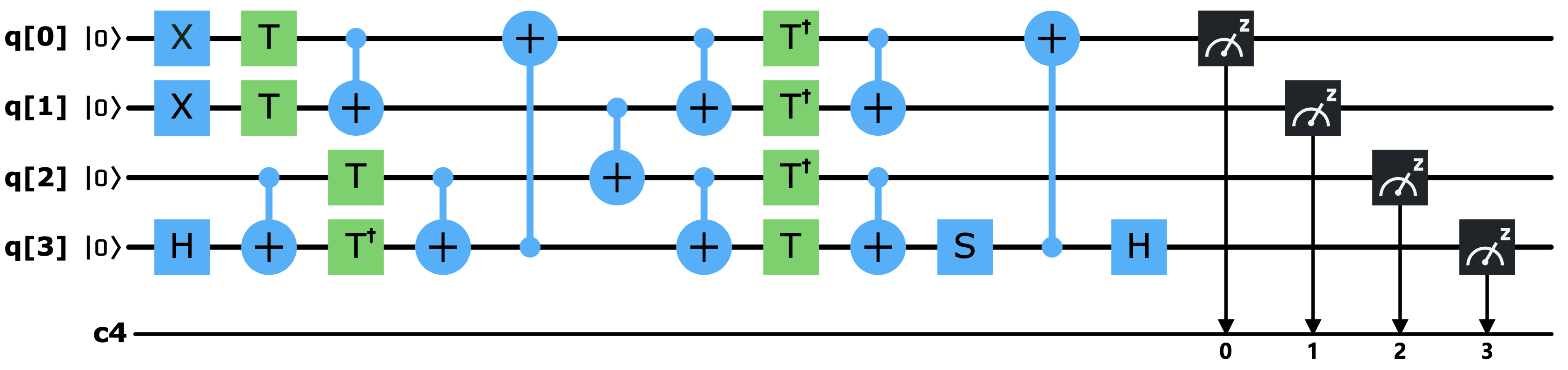
QASMBench is an OpenQASM benchmark suite for NISQ evaluation. The .qasm code can be directly loaded in IBM Quantum Experience for execution. Please see our (paper or arXiv) for details.
Latest version: 1.3
The rapid development of quantum computing (QC) in the NISQ era urgently demands a light-weighted, low-level benchmark suite and insightful evaluation metrics for characterizing the properties of prototype NISQ devices, the efficiency of QC programming compilers, schedulers and assemblers, and the capability of quantum simulators in a classical computer. We propose QASMBench as a low-level, easy-to-use benchmark suite based on the OpenQASM assembly representation. It consolidates commonly used quantum routines and kernels from a variety of domains including chemistry, simulation, linear algebra, searching, optimization, arithmetic, machine learning, fault tolerance, cryptography, etc., trading-off between generality and usability. Most of the QASMBench application code can be launched and verified in IBM-Q directly. For simulation purposes, you may also want to use our State-Vector simulator (SV-Sim) and Density-Matrix simulator (DM-Sim) to run on GPU/CPU HPC clusters.
To analyze these kernels in terms of NISQ device execution, in addition to circuit width and depth, we propose four circuit metrics including gate density, retention lifespan, measurement density, and entanglement variance, to extract more insights about the execution efficiency, the susceptibility to NISQ error, and the potential gain from machine-specific optimizations. We provide script under the metric folder to analyze the OpenQASM circuit and report the metrics we defined.
Depending on the number of qubits used, QASMBench includes three categories. For the introduction of the benchmarking routines under each category, please see our paper for detail. For each benchmark in the following tables, we list its name, brief description, and the algorithm category it belongs to, which is based on this Nature paper by adding the categories of quantum arithmetic, quantum machine learning and quantum communication.
The 'Gates' here refers to the number of Standard OpenQASM gates (see our paper) but excluding those gates in a branching if statement. It is known that physical qubits in an NISQ device follow a certain topology. Since the 2-qubit gates such as CNOT or CX can only be performed between two adjacent physical qubits, a series of SWAP operations can be required to move the relevant qubits until they become directly-connected. This is an important issue in machine-specific mapping and optimization, implying a significant potential overhead. Consequently, we also list the number of CNOT gates in the tables.
Qunatum circuits using 2 to 5 qubits.
| Benchmark | Description | Algorithm | Qubits | Gates | CNOT | Reference |
|---|---|---|---|---|---|---|
| wstate | W-state preparation and assessment | Logical Operation | 3 | 30 | 9 | OpenQASM |
| adder | Quantum ripple-carry adder | Quantum Arithmetic | 4 | 23 | 10 | Scaffold |
| basis_change | Transform the single-particle baseis of an linearly connected electronic structure | Quantum Simulation | 3 | 53 | 10 | OpenFermion |
| basis_trotter | Implement Trotter steps for molecule LiH at equilibrium geometry | Quantum Simulation | 4 | 1626 | 582 | OpenFermion |
| cat_state | Coherent superposition of two coherent states with opposite phase | Logical Operation | 4 | 4 | 3 | Scaffold |
| deutsch | Deutsch algorithm with 2 qubits for f(x) = x | Hidden Subgroup | 2 | 5 | 1 | OpenQASM |
| error_correctiond3 | Error correction with distance 3 and 5 qubits | Error Correction | 5 | 114 | 49 | Ref |
| fredkin | Controlled-swap gate | Logical Operation | 3 | 19 | 8 | Scaffold |
| grover | Grover’s algorithm | Search and Optimization | 2 | 16 | 2 | AgentANAKIN |
| hs4 | Hidden subgroup problem | Hidden Subgroup | 4 | 28 | 4 | Scaffold |
| inverseqft | Performs an exact inversion of quantum Fourier tranform | Hidden Subgroup | 4 | 8 | 0 | OpenQASM |
| ipea | Iterative phase estimation algorithm | Hidden Subgroup | 2 | 68 | 30 | OpenQASM |
| iswap | An entangling swapping gate | Logical Operation | 2 | 9 | 2 | OpenQASM |
| linearsolver | Solver for a linear equation of one qubit | Linear Equation | 3 | 19 | 4 | Ref |
| lpn | Learning parity with noise | Machine Learning | 5 | 11 | 2 | sampaio96 |
| pea | Phase estimation algorithm | Hidden Subgroup | 5 | 98 | 42 | OpenQASM |
| qec_sm | Repetition code syndrome measurement | Error Correction | 5 | 5 | 4 | OpenQASM |
| qft | Quantum Fourier transform | Hidden Subgroupe | 4 | 36 | 12 | OpenQASM |
| qec_en | Quantum repetition code encoder | Error Correction | 5 | 25 | 10 | sampaio96 |
| teleportation | Quantum teleportation | Quantum Communication | 3 | 8 | 2 | Ref |
| toffoli | Toffoli gate | Logical Operation | 3 | 18 | 6 | Scaffold |
| variational | Variational ansatz for a Jellium Hamiltonian with a linear-swap network | Quantum Simulation | 4 | 54 | 16 | OpenFermion |
| vqe_uccsd | Variational quantum eigensolver with UCCSD | Linear Equation | 4 | 220 | 88 | Scaffold |
| shor | Shor’s algorithm | Hidden Subgroup | 5 | 64 | 30 | Qiskit |
| bell | Circuit equivalent to Bell inequality test | Logic Operation | 4 | 33 | 7 | Cirq |
| qrng | Quantum random number generator | Quantum Arithmetic | 4 | 4 | 0 | Paper, Repo |
| qaoa | Quantum approximate optimization algorithm | Search and Optimization | 3 | 15 | 6 | Repo |
| quantumwalks | Quantum walks on graphs with up to 4 nodes | Quantum Walk | 2 | 11 | 3 | Repo |
| dnn | 3 layer quantum neural network sample | Machine Learning | 2 | 226 | 42 | Ref |
Quantum circutis using 6 to 15 qubits.
| Benchmark | Description | Algorithm | Qubits | Gates | CNOT | Reference |
|---|---|---|---|---|---|---|
| adder | Quantum ripple-carry adder | Quantum Arithmetic | 10 | 142 | 65 | OpenQASM |
| bv | Bernstein-Vazirani algorithm | Hidden Subgroup | 14 | 41 | 13 | OpenQASM |
| cc | Counterfeit coin finding problem | Search and Optimization | 12 | 22 | 11 | OpenQASM |
| ising | Ising model simulation via QC | Quantum Simulation | 10 | 480 | 90 | Scaffold |
| multiply | Performing 3×5 in a quantum circuit | Quantum Arithmetic | 13 | 98 | 40 | AgentANAKIN |
| qf21 | Using quantum phase estimation to factor the number 21 | Hidden Subgroup | 15 | 311 | 115 | AgentANAKIN |
| qft | Quantum Fourier transform | Hidden Subgroup | 15 | 540 | 210 | OpenQASM |
| qpe | Quantum phase estimation algorithm | Hidden Subgroup | 9 | 123 | 43 | AgentANAKIN |
| sat | Boolean satisfiability problem | Search and Optimization | 11 | 679 | 252 | OpenQASM |
| seca | Shor's error correction algorithm for teleportation | Error Correction | 11 | 216 | 84 | AgentANAKIN |
| simons | Simon’s algorithm | Hidden Subgroup | 6 | 44 | 14 | AgentANAKIN |
| vqe_uccsd | Variational quantum eigensolver with UCCSD | Linear Equation | 6 | 2282 | 1052 | Scaffold |
| vqe_uccsd | Variational quantum eigensolver with UCCSD | Linear Equation | 8 | 10808 | 5488 | Scaffold |
| qaoa | Quantum approximate optimization algorithm | Search and Optimization | 6 | 270 | 54 | Cirq |
| bb84 | A quantum key distribution circuit | Quantum Communication | 8 | 27 | 0 | Cirq |
| multiplier | Quantum multiplier | Quantum Arithmetic | 15 | 574 | 246 | Cirq |
| dnn | 16-dimension quantum neural network sample | Machine Learning | 8 | 1008 | 192 | Ref |
Quantum circuits using more than 15 qubits.
| Benchmark | Description | Algorithm | Qubits | Gates | CNOT | Reference |
|---|---|---|---|---|---|---|
| dnn | quantum neural network sample | Machine Learning | 16 | 2016 | 384 | Ref |
| bigadder | Quantum ripple-carry adder | Quantum Arithmetic | 18 | 284 | 130 | OpenQASM |
| cc | Counterfeit coin finding problem via QC | Hidden Subgroup | 18 | 34 | 17 | OpenQASM |
| bv | Bernstein-Vazirani algorithm | Hidden Subgroup | 19 | 56 | 18 | OpenQASM |
| qft | Quantum Fourier tranform | Hidden Subgroup | 20 | 970 | 380 | OpenQASM |
| bwt | Binary Welded Tree: a quantum walk algorithm in continuous time domain | Quantum Walk | 21 | 462001 | 174800 | QASMBench |
| cat_state | Coherent superposition of two coherent states with opposite phase | Logical Operation | 22 | 22 | 21 | QASMBench |
| ghz_state | Greenberger-Horne-Zeilinger (GHZ) state for max entanglement | Logical Operation | 23 | 23 | 22 | QASMBench |
| ising | Ising model simulation via QC | Quantum Simulation | 26 | 280 | 50 | QASMBench |
| multiplier | Quantum multiplier | Quantum Arithmetic | 25 | 1743 | 750 | Cirq |
| square_root | Computing the square root of an number via amplitude amplification | Quantum Arithmetic | 18 | 2300 | 898 | Scaffold |
| swap_test | Swap test to measure quantum state distance | Machine Learning | 25 | 230 | 96 | QASMBench |
| vqe | Variational quantum eigensolver with UCCSD | Quantum Simulation | 24 | 2306072 | 1538240 | QASMBench |
| ising | Ising model simulation via QC | Quantum Simulation | 500 | 5494 | 998 | Scaffold |
| ising | Ising model simulation via QC | Quantum Simulation | 1000 | 10994 | 1998 | Scaffold |
| class_number | Compute the class group of a real quadratic number field | Hidden Subgroups | 60052 | 31110504 | 12460637 | Scaffold |
OpenQASM header file that defines all the gates. Please see OpenQASM and our paper for details.
Each benchmark folder include the following file:
- bench.qasm: OpenQASM source file.
- bench.png: Visualization of the circuit from IBM QE.
- res_bench.png: Running results from IBM QE quantum backends (mainly 5-qubit Burlington, 15-qubit Melbourne, and 27-qubit Paris).
The QASMBench circuits can be directly uploaded and verified on IBM-Q NISQ quantum device.
You may also want to use our state-vector and density-matrix quantum circuit simulator (SV-Sim and DM-Sim) for simulating the QASMBench benchmark circuits efficiently on modern CPU (Intel X86, AMD X86, IBM Power), GPU (NVIDIA GPU and AMD GPU) and Xeon-Phi workstations or HPC clusters (e.g., ORNL Summit/Frontier, ANL Theta, and NERSC Cori/Perlmutter Supercomputers).
We propose a set of circuit based evaluation metrics representing various features of a quantum application. These metrics are designed such that through them certain estimation can be performed on executing a particular circuit over a particular NISQ device. The metrics serve as useful indicators on how a quantum circuit can stress a NISQ hardware device. Please see our paper for the math formula and analysis.
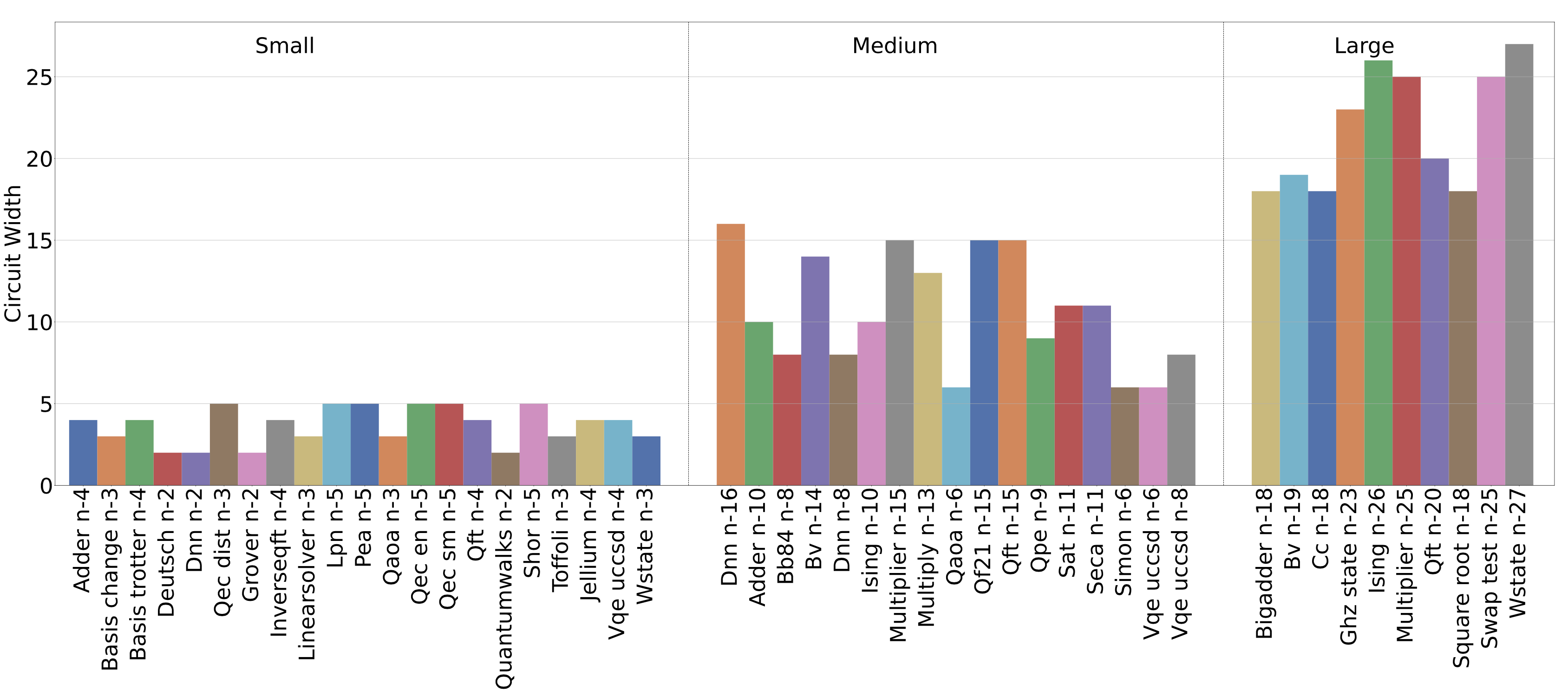
Circuit width is defined as the number of qubits that enter the superposition state at least once within an application’s lifespan. Qubits that are measured in the interim of a circuit and re-enter superposition are only counted as one qubit towards the circuit width. Circuit width dictates the spatial capacity required for a quantum device in order to run the quantum circuit. The following figure show the circuit width of QASMBench:
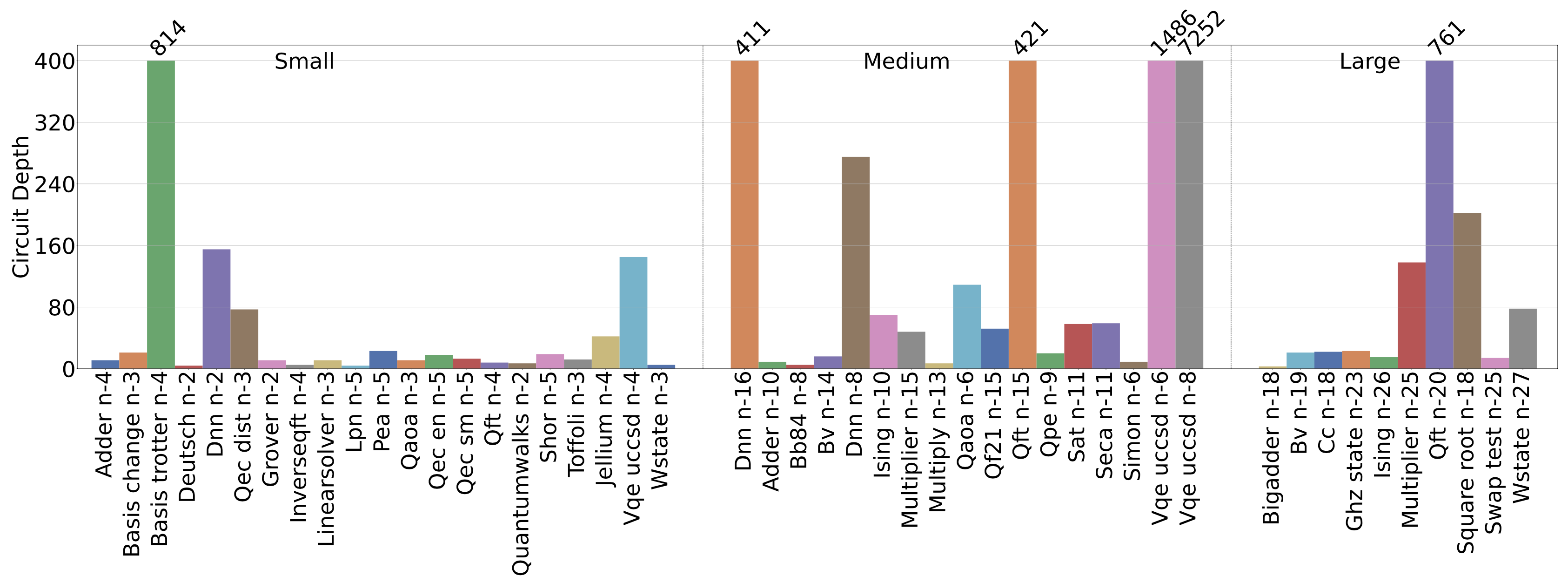
Circuit depth is defined as the minimum time-evolution steps required to complete a quantum application. Time evolution is the process of completing all gates defined at time T=T(j), and once these are completed, the circuit moves onto time T = T(j+1), where the following gates are to be processed. Circuit depth can be computed by decomposing OpenQASM code into a n(q) x T matrix Q, where Q(q(i),t(j)) is the time-evolution steps to complete the gate on qubit i at time j. The sum of the maximum time in each column is then equal to the minimum time required for a quantum application. The following figure show the circuit depth of QASMBench:
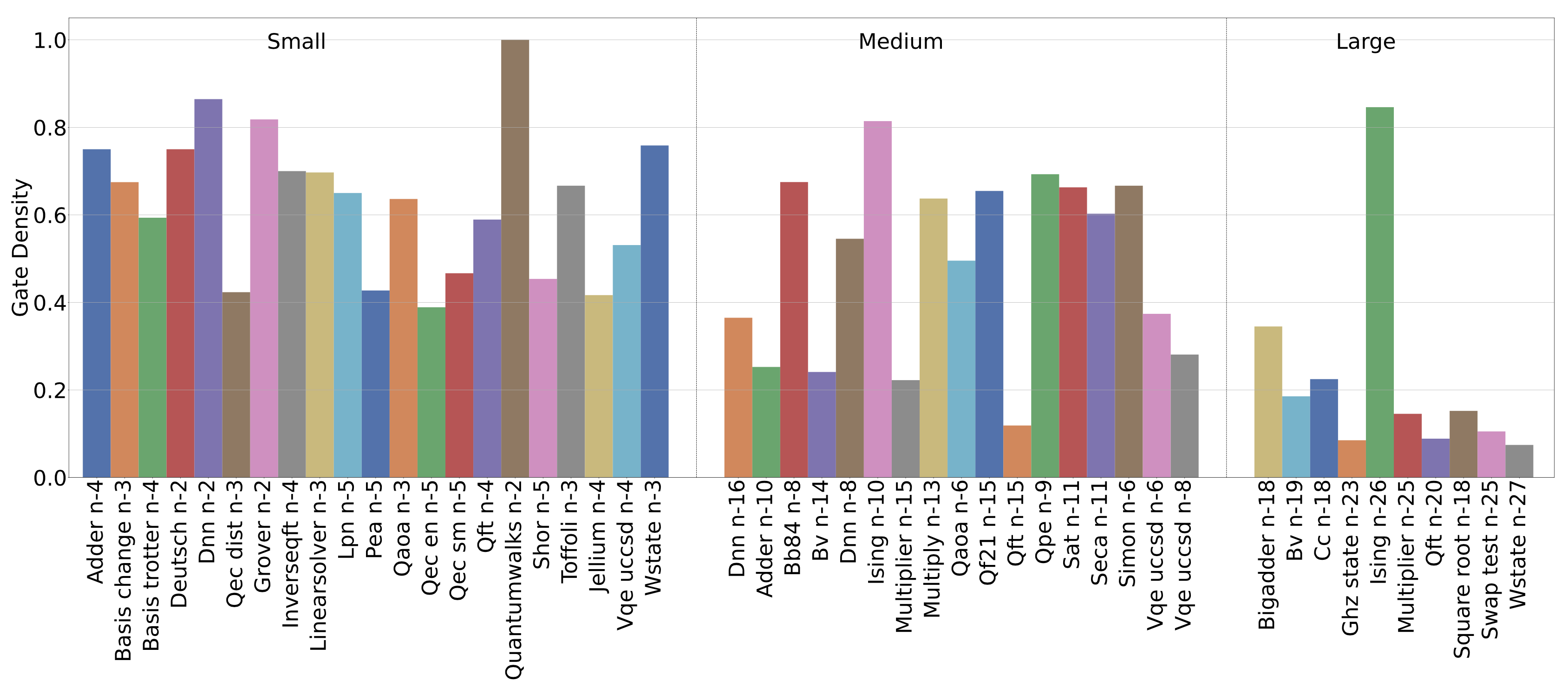
Gate density, or operation density, describes the occupancy of gate slots along the time-evolution steps of a quantum circuit. As certain qubits might need to wait for other qubits in the time evolution (i.e, gate dependency), they remain idle by executing the identity gate (ID gate). Consequently, if a gate slot is empty due to dependency, it implies a lower occupancy for the quantum hardware. This is similar to a classical processor, where data dependency introduces pipeline bubbles and reduced occupancy. We propose Gate Density to measure the likely occupancy of a circuit when mapping to a quantum hardware. The following figure show the gate density of QASMBench:
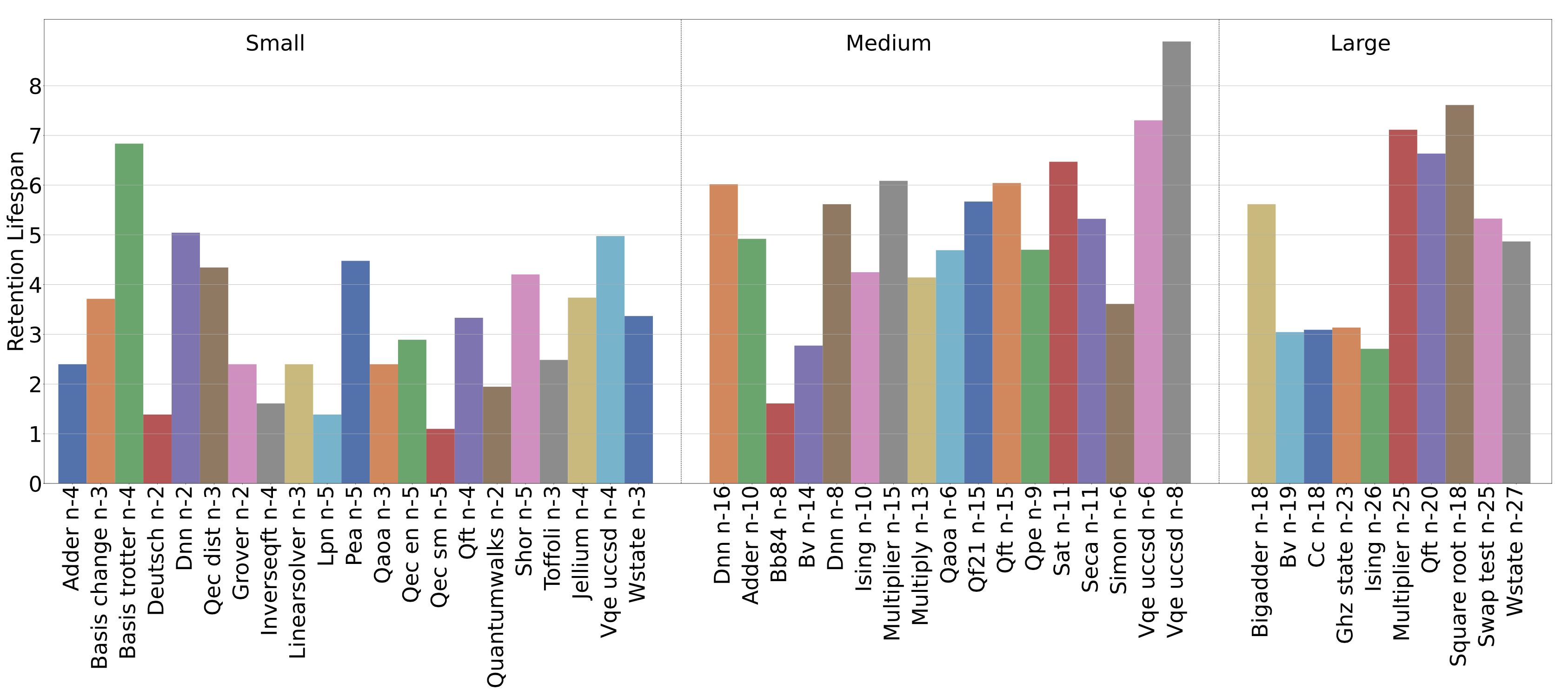
Retention Lifespan describes the maximum lifespan of a qubit within a system, and is motivated by the T1 and T2 coherence time of a quantum device. A longer lifespan of a quantum system implies more decay to the ground state (T1) and state-transition due to environment noise (T2), thus is more susceptible to information loss. Therefore, we propose taking the qubit with the longest lifespan to determine the system’s retention lifespan. Using this metric, one can estimate if a particular circuit can be executed in a NISQ device with high fidelity, given its T1/T2 coherence time. Note, all IBM-Q machines offer T1/T2 coherence time as status indicators for the hardware. As circuit depth can grow substantially, we introduce the log operator to shrink the scale. The following figure show the retention lifespan of QASMBench:
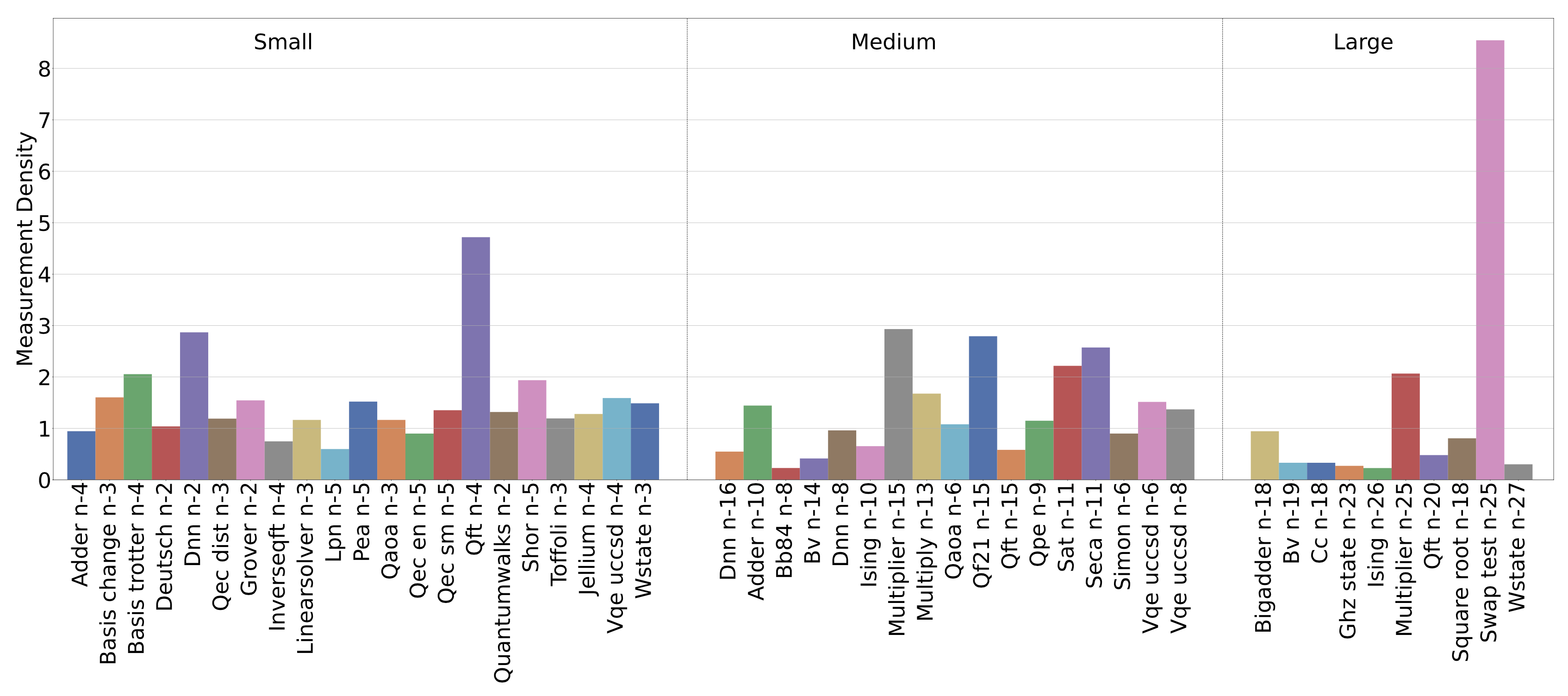
Measurement density assesses the importance of measurements in a circuit. A higher measurement count implies the fact that each measurement might be of relatively less importance (e.g., periodic measurement in QEC, or measurement over ancilla qubits), whereas for application with less measurements, the measurement may be of utmost importance. The importance also increases when a measurement accounts for a wider and/or deeper circuit. A good example is the SWAP test, where the circuit can be very large but only one measurement is taken to report the similarity. Consequently, this measurement is extremely important to the application. Since the circuit depth/width can be large and the importance of measurement decays when circuit depth/width keeps on increasing, we add a log to shrink the scale. The following figure show the retention lifespan of QASMBench:
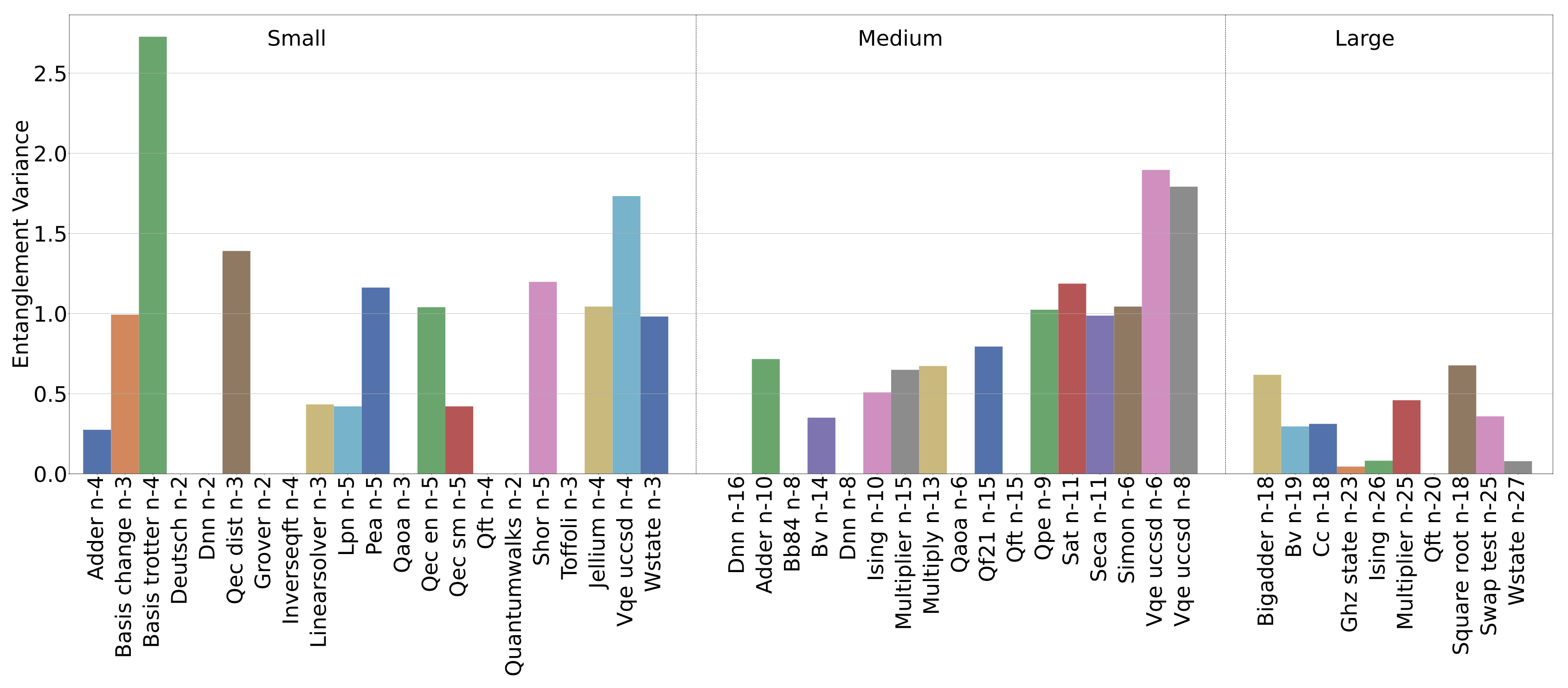
Entanglement Variance measures the balance of entanglement across the qubits of a circuit. Circuits with a higher Entanglement Variance indicate that certain qubits are more connected than other qubits (i.e., using more 2-qubit gates such as CX than others). This metric implies that when the circuit is mapped to a NISQ device: (i) less SWAP gates are needed if those hotspot qubits are mapped to the central vertices in the NISQ device topology, such as Qubit-1 in ibmq-belem and Qubit-2 in ibmq-yorkton). A higher entanglement variance implies a higher potential benefit from a good logic-physical qubit-mapping through quantum transpilation. If the entanglement variance is zero, little benefit should be expected from a better transpilation strategy; (ii) Given 2-qubit gate is one of the major sources introducing error, a higher Entanglement Variance implies uneven error introduction among qubits. The following figure show the entanglement variance of QASMBench:
OpenQASM (Open Quantum Assembly Language) is a low-level quantum intermediate representation (IR) for quantum instructions, similar to the traditional Hardware-Description-Language (HDL) like Verilog and VHDL. OpenQASM is the open-source unified low-level assembly language for IBM quantum machines publically available on cloud that have been investigated and verified by many existing research works. Several popular quantum software frameworks use OpenQASM as one of their output-formats, including Qiskit, Cirq, Scaffold, ProjectQ, etc.
The Quantum Information Software Kit (Qiskit) is a quantum software developed by IBM. It is based on Python. OpenQASM can be generated from Qiskit via:
QuantumCircuit.qasm()
Cirq is a quantum software framework from Google. OpenQASM can be generated from Cirq (not fully compatible) via:
cirq.Circuit.to_qasm()
Scaffold is a quantum programming language embedded in the C/C++ programming language based on the LLVM compiler toolchain. A Scaffold program can be compiled by Scaffcc to OpenQASM via "-b" compiler option.
ProjectQ is a quantum software platform developed by Steiger et al. from ETH Zurich. The official website is here. ProjectQ can generate OpenQASM when using IBM quantum machines as the backends:
IBMBackend.get_qasm()
Ang Li, Pacific Northwest National Laboratory (PNNL)
Samuel Stein, Pacific Northwest National Laboratory (PNNL)
Sriram Krishnamoorthy, Pacific Northwest National Laboratory (PNNL)
James Ang, Pacific Northwest National Laboratory (PNNL)
And also the original authors that developed these quantum routines.
For research articles, please cite our paper:
- Ang Li, Samuel Stein, Sriram Krishnamoorthy and James Ang, "QASMBench: A Low-level QASM Benchmark Suite for NISQ Evaluation and Simulation" [arXiv:2005.13018].
Bibtex:
@article{li2021qasmbench,
title={QASMBench: A Low-level QASM Benchmark Suite for NISQ Evaluation and Simulation},
author={Li, Ang and Stein, Samuel and Krishnamoorthy, Sriram and Ang, James},
journal={arXiv preprint arXiv:2005.13018},
year={2021}
}
This project is licensed under the BSD License, see LICENSE file for details.
We thank the many developers and open-source community for providing these awesome quantum circuits online so we are able to collect and form this benchmark suite.
PNNL-IPID: 31924-E, IR: PNNL-SA-153380, PNNL-SA-162867, ECCN:EAR99
This work is supported by U.S. DOE Co-design Center for Quantum Advantage (C2QA) Quantum Information Science (QIS) center XCITe crosscut. The Pacific Northwest National Laboratory (PNNL) is operated by Battelle for the U.S. Department of Energy (DOE) under contract DE-AC05-76RL01830.
Please contact us If you'd like to add your circuits into the benchmark suite or you'd like to remove your circuits from the suite.