GAN: generative adversarial nets; MMD: maximum mean discrepancy; TF: TensorFlow
This repository contains codes for MMD-GAN and the repulsive loss proposed in ICLR paper [1]:
Wei Wang, Yuan Sun, Saman Halgamuge. Improving MMD-GAN Training with Repulsive Loss Function. ICLR 2019. URL: https://openreview.net/forum?id=HygjqjR9Km.
The code defines the neural network architecture as dictionaries and strings to ease test of different models. It also contains many other models I have tried, so sorry if you find it a little bit confusing.
The structure of code:
- DeepLearning/my_sngan/SNGan defines how a general GAN model is trained and evaluated.
- GeneralTools contains various tools:
- graph_func contains functions to run a model graph and metrics for evaluating generative models (Line 1595).
- input_func contains functions to handle datasets and input pipeline.
- layer_func contains functions to convert network architecture dictionary to operations
- math_func defines various mathematical operations. You may find spectral normalization at Line 397, loss functions for GAN at Line 2088, repulsive loss at Line 2505, repulsive with bounded kernel (referred to as rmb) at Line 2530.
- misc_fun contains FLAGs for the code.
- my_test_ contain the specific model architectures and hyperparameters.
- Modify GeneralTools/misc_func accordingly;
- Read Data/ReadMe.md; download and prepare the datasets;
- Run my_test_ with proper hyperparameters.
Here we introduce the algorithms and tricks.
The paper [1] proposed three methods:
- Repulsive loss
where - real samples,
- generated samples,
- kernel formed by the discriminator
and kernel
. The discriminator loss of previous MMD-GAN [2], or what we called attractive loss, is
.
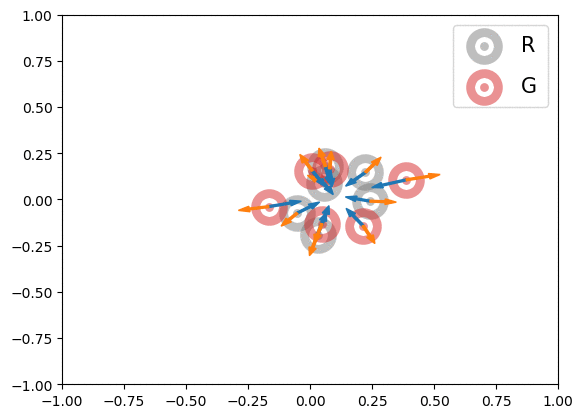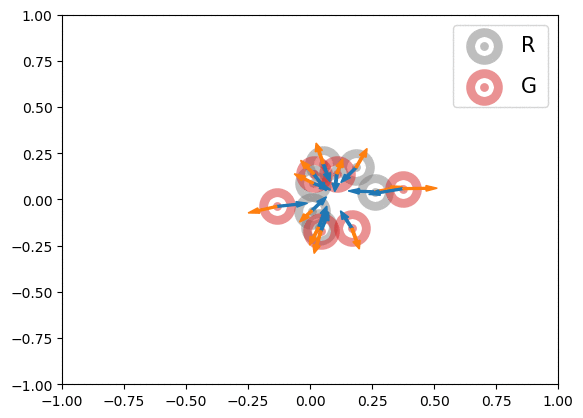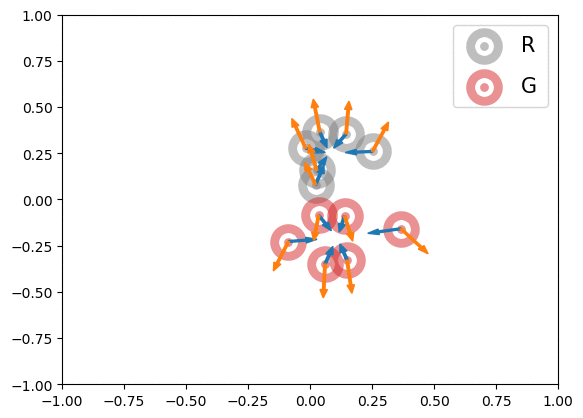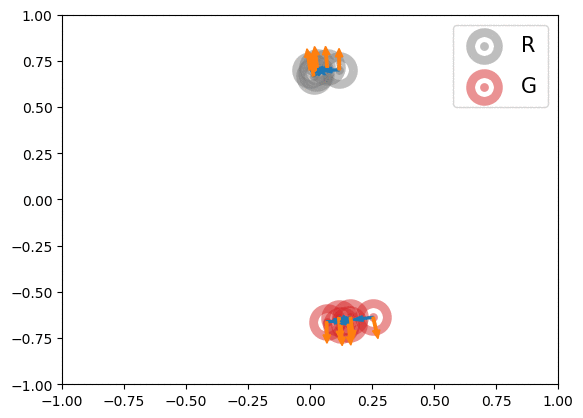
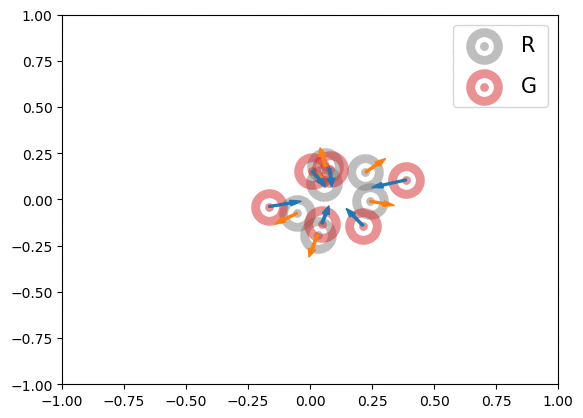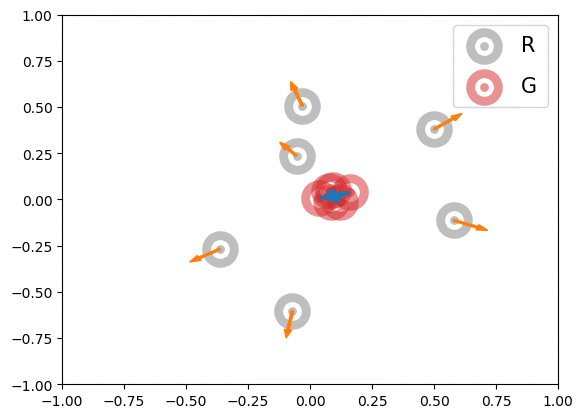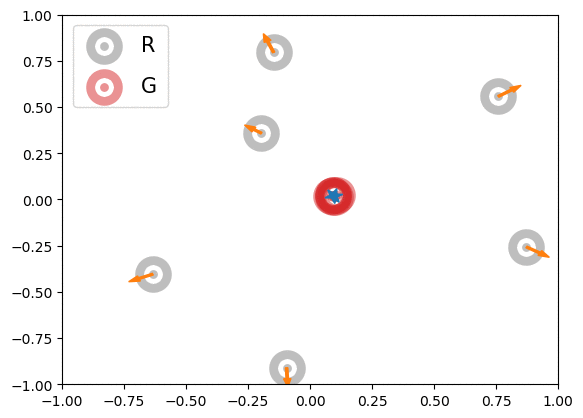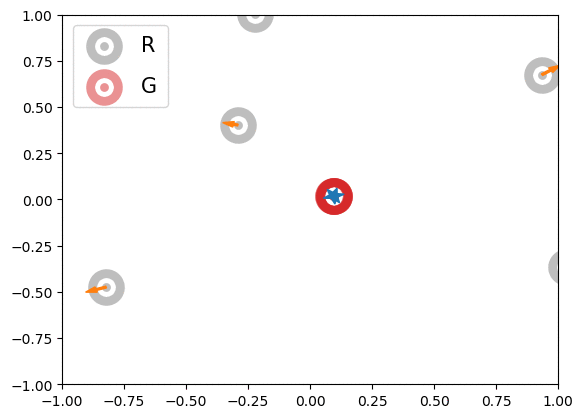
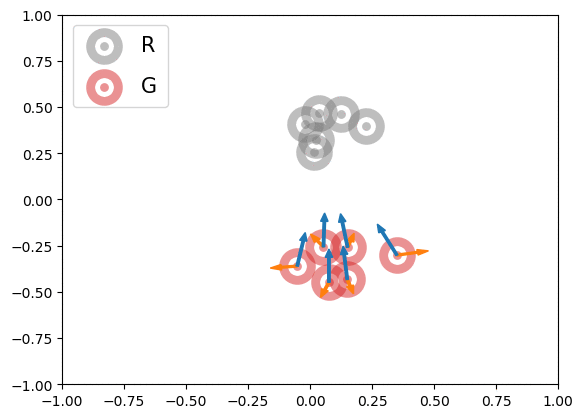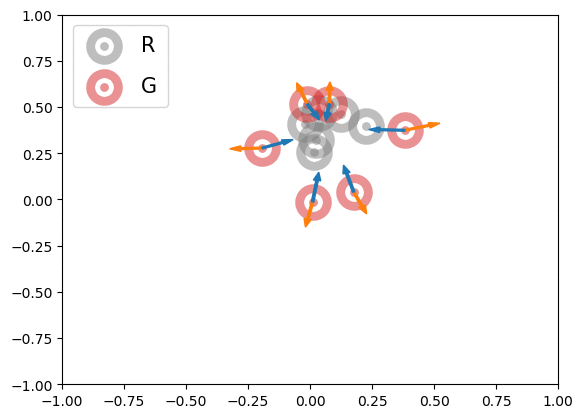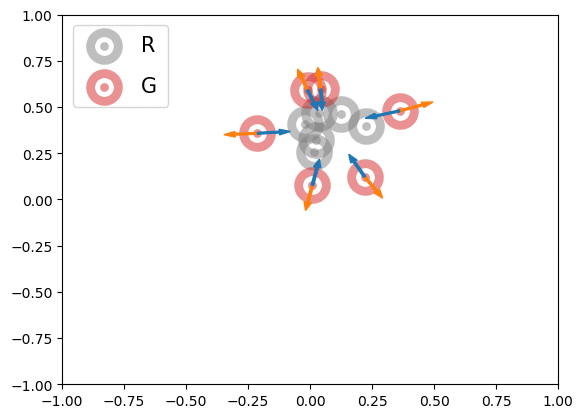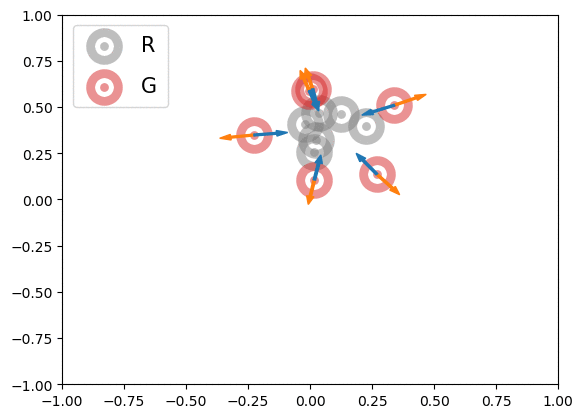
Below is an illustration of the effects of MMD losses on free R(eal) and G(enerated) particles (code in Figures folder). The particles stand for discriminator outputs of samples, but, for illustration purpose, we allow them to move freely. These GIFs extend the Figure 1 of paper [1].
 |
 |
 |
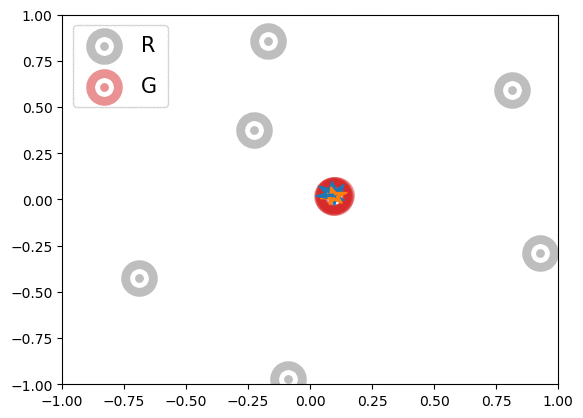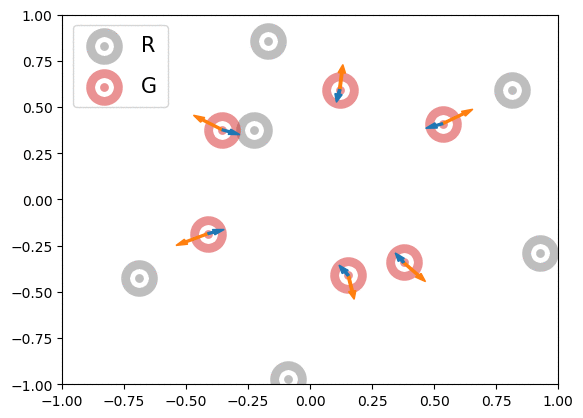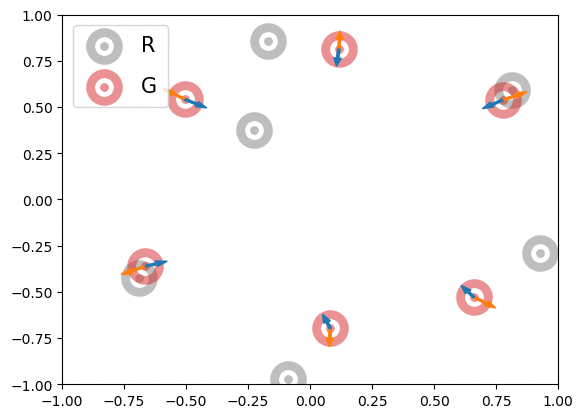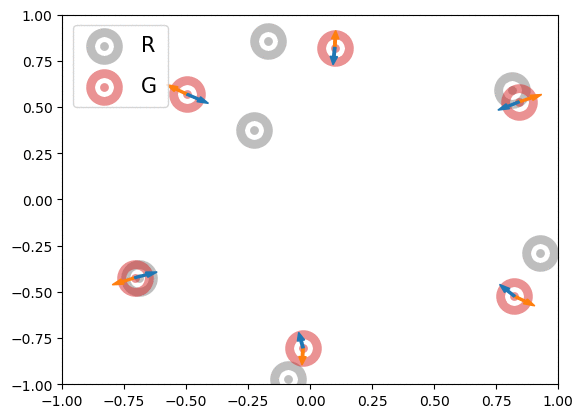 |
In the first row, we randomly initialized the particles, and applied or
for 600 steps. The velocity of each particle is
. In the second row, we obtained the particle positions at the 450th step of the first row and applied
for another 600 steps with velocity
. The blue and orange arrows stand for the gradients of attractive and repulsive components of MMD losses respectively. In summary, these GIFs indicate how MMD losses may move the free particles. Of course, the actual case of MMD-GAN is much more complex as we update the model parameters instead of output scores directly and both networks are updated at each step.
We argue that may cause opposite gradients from attractive and repulsive components of both
and
during training, and thus slow down the training process. Note this is different from the end-stage training when the gradients should be opposite and cancelled out to reach 0. Another way of interpretation is that, by minimizing
, the discriminator maximizes the similarity between the outputs of real samples, which results in D focusing on the similarities among real images and possibly ignoring the fine details that separate them. The repulsive loss
actively learns such fine details to make real sample outputs repel each other.
The gradient of Gaussian kernel is near 0 when the input distance is too small or large. The bounded kernel avoids kernel saturation by truncating the two tails of distance distribution, an idea inspired by the hinge loss. This prevents the discriminator from becoming too confident.
- Power iteration for convolution (used in spectral normalization)
At last, we proposed a method to calculate the spectral norm of convolution kernel. At iteration t, for convolution kernel , do
,
, and
. The spectral norm is estimated as
.
We recommend using the following tricks.
- Spectral normalization, initially proposed in [3]. The idea is, at each layer, to use
for convolution/dense multiplication. Here we multiply the signal with a constant
after each spectral normalization to compensate for the decrease of signal norm at each layer. In the main text of paper [1], we used
empirically. In Appendix C.3 of paper [1], we tested a variety of
values.
- Two time-scale update rule (TTUR) [4]. The idea is to use different learning rates for the generator and discriminator.
Unlike the case of Wasserstein GAN, we do not encourage using the repulsive loss for discriminator or the MMD loss for generator
to indicate the progress of training. You may find that, during the training process,
- both
and
may be close to 0 initially; this is because both G and D are weak.
may gradually increase during training; this is because it becomes harder for G to generate high quality samples and fool D (and G may not have the capacity to do so).
For balanced and capable G and D, we would expect both and
to stay close to 0 during the whole training process and any kernel (i.e.,
,
and
) to be away from 0 or 1 and stay in the middle (e.g., 0.6).
In some cases, you may find training using the repulsive loss diverges. Do not panic. It may be that the learning rate is not suitable. Please try other learning rate or the bounded kernel.
Thank you for reading!
Please feel free to leave comments if things do not work or suddenly work, or if exploring my code ruins your day. :)
[1] Wei Wang, Yuan Sun, Saman Halgamuge. Improving MMD-GAN Training with Repulsive Loss Function. ICLR 2019. URL: https://openreview.net/forum?id=HygjqjR9Km.
[2] Chun-Liang Li, Wei-Cheng Chang, Yu Cheng, Yiming Yang, and Barnabas Poczos. MMD GAN: Towards deeper understanding of moment matching network. In NeurIPS, 2017.
[3] Takeru Miyato, Toshiki Kataoka, Masanori Koyama, and Yuichi Yoshida. Spectral normalization
for generative adversarial networks. In ICLR, 2018.
[4] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. GANs Trained by a Two Time-Scale Update Rule Converge to a Nash Equilibrium. In NeurIPS, 2017.