hexutil

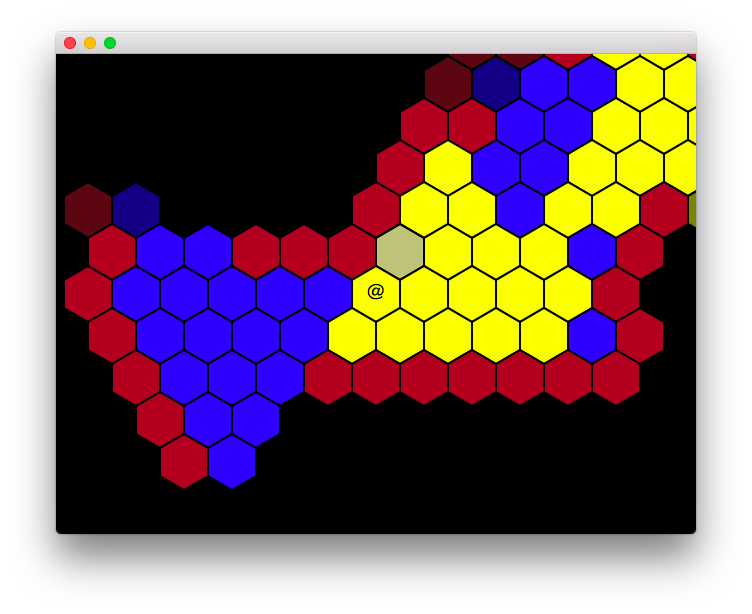
Classes and functions to deal with hexagonal grids.

Introduction

This module provides the following functionality.

Manipulation of grid coordinates in a hexagonal grid.
Converting between hexagonal grid coordinates and screen coordinates.
Field-of-view calculation on a hexagonal grid.
A* path-finding on a hexagonal grid.

All this is provided by the module hexutil. The file example.py contains example coding using this functionality. The above image is a screenshot from this example.

Manipulation of grid coordinates in a hexagonal grid.

The class hexagon.Hex represents a particular hexagon in a grid. Class Hex takes two integer arguments, x and y. These need to satisfy the property that their sum is even.

The following (x,y) coordinate system is used to address hexagons in the grid.

At first, it may seem weird that this coordinate system leaves "holes" in the representation, i.e. there is no hexagon corresponding to, say, (0, 1). However, that turns out to be not a real problem in practise. The advantage is that relationship to the actual center points of the hexagons becomes very simple, namely, just multiply y with √3. This also simplifies screen coordinate calculations.

The only time the "holes" are an issue is if you want to pack grid data densely into a 2D (numpy) array or a list-of-lists. In that case, just use ar[hexagon.x//2][hexagon.y] to index into array ar.

The constructor of Hex checks the "x+y is even" property. If it is not satisfied, an InvalidHex exception is thrown.

Note that Hex is a namedtuple. That means that it can be used wherever a 2-tuple (x, y) is required. It also means that is is immutable.

Important functionality on instances of Hex.

The hex.x and hex.y fields for accessing the x- and y-coordinate, respectively.
Arithmetic operations hex1 + hex2, hex1 - hex2 and - hex are supported.
The method hex.neighbours() returns the 6 direct neighbours of a hex.
The method hex1.distance(hex2) returns the distance in terms of steps on the hexagon grid between hex1 and hex2.

Converting between hexagonal grid coordinates and screen coordinates.

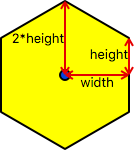
The mapping of a hexagon to screen (pixel) coordinates can be described by two parameters width and height. The following image shows how these relate to the hexagon size.

For a perfectly regular hexagon, the relationship height = ⅓√3 width should hold. In practice, we typically want integral pixel coordinates.

The class HexGrid captures such a pair of width and height values. It can be initialized as HexGrid(width, height) or HexGrid(width). In the latter case, height is automatically computed as round(⅓√3 * width).

Important functionality on instances of Hex.

The hexgrid.width and hexgrid.height fields for accessing the width and height, respectively.
Method hexgrid.center(hex) returns a pair (x, y) of screen coordinates of the center of hex.
Method hexgrid.corners(hex) returns a sequence of 6 pairs (x, y) of screen coordinates of the 6 corners of hex.
Method hexgrid.bounding_box(hex) returns a hexutil.Rectangle object describing the bounding box of hex.
Method hexgrid.hex_at_coordinate(x, y) returns the Hex at screen coordinate (x,y).
Method hexgrid.hexes_in_rectangle(rect) returns a sequence of all Hex-es which overlap with Rectangle rect.

Field-of-view calculation on a hexagonal grid.

Field-of-view calculation is done by the following method on Hex instances.

hex.field_of_view(self, transparent, max_distance, visible=None)

transparent -- from a Hex to a boolean, indicating of the Hex is transparent
max_distance -- maximum distance you can view
visible -- if provided, should be a dict which will be filled and returned

Returns a dict which has as its keys the hexagons which are visible. The value is a bitmask which indicates which sides of the hexagon are visible. The bitmask is useful if you want to use this function also to compute light sources.

view_set = player_pos.field_of_view(...)
light_set = light_source.field_of_view(...)

# Is pos visible?
if view_set.get(pos, 0) & light_set.get(pos, 0):
    # yes it is

A* path-finding on a hexagonal grid.

Path-finding (using the A* algorithm) is done by the following method on Hex instances.

hex.find_path(self, destination, passable, cost=lambda pos: 1)

hex -- Starting position (Hex object) for path finding.
destination -- Destination position for path finding.
passable -- Function of one position, returning True if we can move through this hex.
cost -- cost function for moving through a hex. Should return a value ≥ 1. By default all costs are 1.