Source code for "Space-time design for deep joint source channel coding of images Over MIMO channels", SPAWC 2023, https://ieeexplore.ieee.org/document/10304536
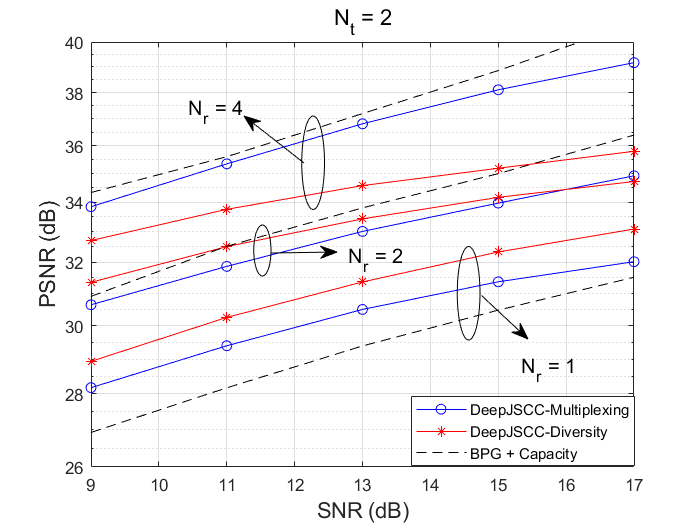
Diversity-Multiplexing trade-off for MIMO systems has been extensively studied in digital communication systems (Zheng & Tse). However, for the emerging semantic communications
there is no prior work exploring this. Thus, we first explore the simplest diversity-multiplexing trade-off for the semantic communications, where the system performance using
orthogonal space-time codes (OSTBC) which represents diversity and the spatial multiplexing scheme representing multiplexing are studied.
It is shown that by using the OSTBC, the diversity system can outperform the multiplexing scheme when
- Python (3.6.9 or above)
- numpy
- pytorch 1.10.0+cu102
- compressai (pip install compressai)
Basically, directly run the 'run.py' will generate the performance of the diversity scheme for a 2x2 MIMO system. To generate the performance for other scenarios, please alternate the parameters in 'get_args.py'.
E.g., for multiplexing scheme, change the 'args.diversity' to false. args.distributed assumes that the two antennas may belong the
two users (distributed MIMO), for conventional MIMO system, place it to false. Also,
Note that the SNR defination in this repo is different from our another DeepJSCC-MIMO paper (https://arxiv.org/abs/2309.00470), where another one can be implementated via belows lines: `noise_stddev=torch.sqrt(10**(-snr/10)*Nt/2)'.
It is worth mentioning the implementation of the baseline as follows:
We only provide the BPG + MIMO capacity scheme which is because our implementation for digital baseline gives a very bad PSNR performance, thus we only provide the upper bound of all digital schemes by assuming MIMO capacity.
The MIMO Capacity is calculated as
Interested readers can also implement the baseline where the transmitter uses BPG + LDPC + QAM and the receiver employs Sphere decoding + LDPC decoder. Based on our experiments, this gives unstatsifactory results. The sphere decoding block can be found in Matlab builtin function: comm.SphereDecoder.
Thanks for Tung-Tze Yang for providing the codes for the DeepJSCC-Q paper.