Time Series Tokenizer for Transformers inspired by Symbolic Aggregate approXimation (SAX) [ ts-tok ]
This repo is an experimental approach that explores a tokenization method that can efficiently tokenize a time-series, for consumption by a NLP Language Model.
The method was developed as an intuitive way to get an approximate token representation for a time-series, that can be used across time-series while their relative values within a training sequence being preserved and also enabling re-construction of original time-series (with some approximation errors).
The training process used here is a generic training method one would use for a Language Modelling task using Transformers.
Since values of a time-series can vary in a wild range, a transformation that converts the series into a fixed interpretable vocabulary of tokens is required, which is taken care of by the tokenization process. To ensure a fixed vocabulary for all time-series, the tokenization process used in this project involves standardizing and binning each context window seperately to create a sequence of tokens.
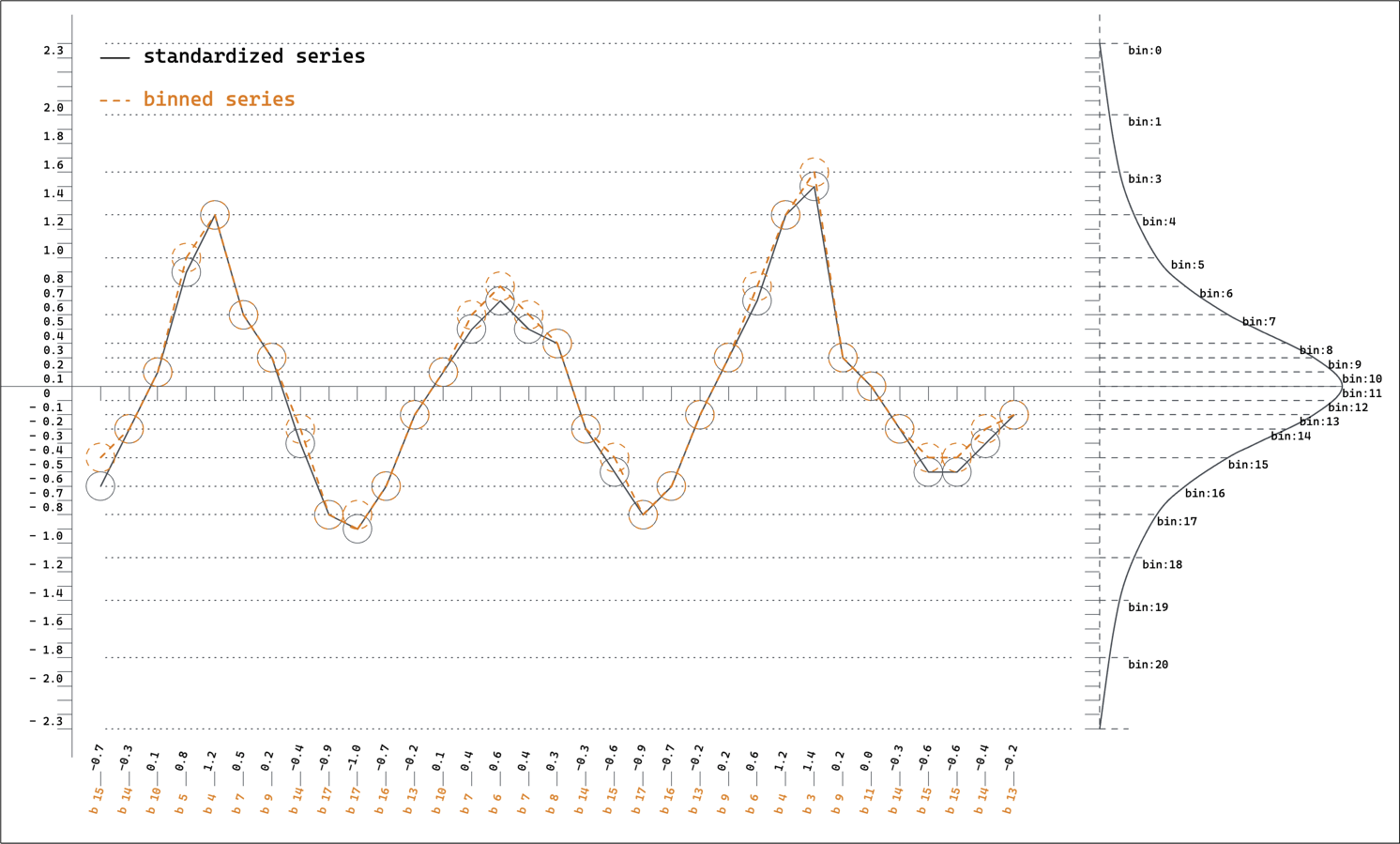Instead of fixed size bins, the bins are created such that each bin holds a fixed percentage of the total data distribution. This in turn means that the bins around the data mean is much smaller, thus this binning reduces reconstruction error introduced by tokenization.
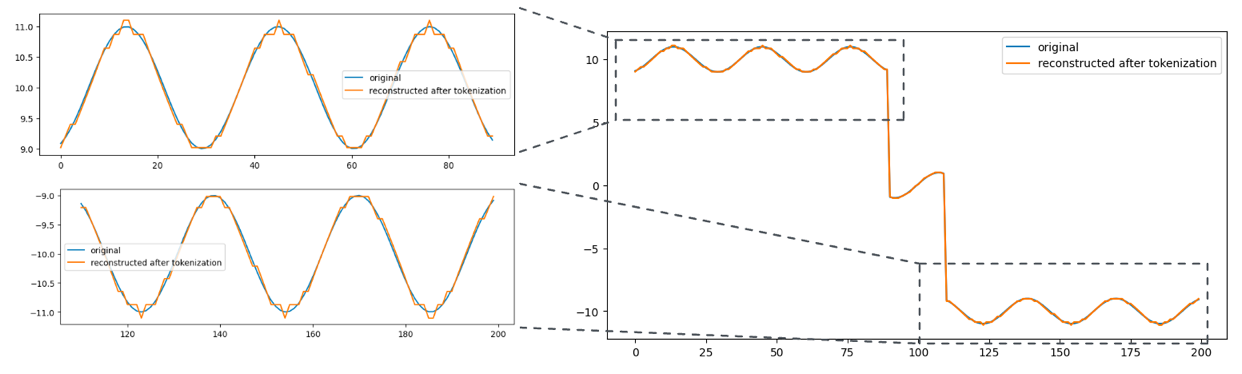This also means that reconstruction is wild for data that do not fit well to gaussians. This is a limitation of the approach, but we believe that this is a reasonable trade-off for the simplicity of the approach.
Gaussian Binning is implemented in tstok.tokenizer.Tokenizer
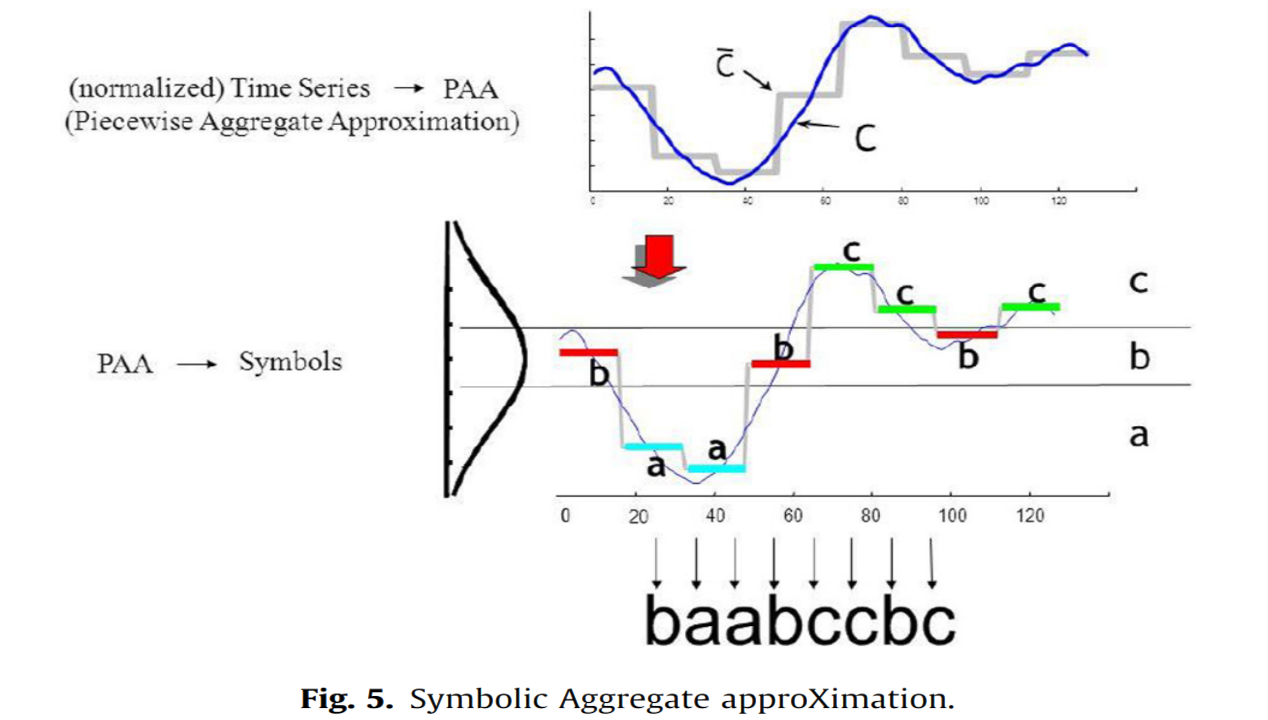Symbolic Aggregate approXimation (SAX) does Gaussian Binning as a specials case, but also does dimensionality reduction. SAX was invented by Dr. Eamonn Keogh of the University of California, Riverside. More details about it can be found here: https://www.cs.ucr.edu/~eamonn/SAX.htm
The targets are also standardized using the same parameters as the context window before being binned. This approach enables forecasting of monotonically increasing/decreasing sequences, even when the context window is not stationary.
Also, the target at sequence position t is normalized using the standardization parameters from the beginning of the context window to sequence position t-1.
example:
context window size = 5
sequence: [V1, V2, V3, V4, V5, V6]
standardized sequence: [v1, v2, v3, v4, v5, v6]
context window:
[v1, v2, v3, v4, v5] --gaussian binning--> [b1, b2, b3, b4, b5]
target window:
[v2, v3, v4, v5, v6] -- standardized --> [s(v2), s(v3), s(v4), s(v5), s(v6)] --gaussian binning--> [b6, b7, b8, b9, b10]
where,
s(v2) = [v1] - (mean([v1]) / std([v1]))
s(v3) = [v1, v2] - (mean([v1, v2]) / std([v1, v2]))
s(v4) = [v1, v2, v3] - (mean([v1, v2, v3]) / std([v1, v2, v3]))
s(v5) = [v1, v2, v3, v4] - (mean([v1, v2, v3, v4]) / std([v1, v2, v3, v4]))
s(v6) = [v1, v2, v3, v4, v5] - (mean([v1, v2, v3, v4, v5]) / std([v1, v2, v3, v4, v5]))
(For getting the standardized value of value v4 in target window, it is standardized using the loc and scale parameters of [v1, v2, v3])
The process of gaussian binning of target window is same as that of context window.
This means that when the value V4 appeared in context window, it was assigned a token b4.
And when it appeared in target window, it was assigned a token b8.
b4 and b8 may or may not be same, depending on the stationarity of the series.
Targe Tokenization is implemented in tstok.data.CustomDataset
The predictions need to be de-tokenized to get the actual time-series value. It's done by first mapping the predicted token id to a bin, and then denormalizing the bin value using parameters of the input series.
This is how a series is tokenized for inference, and how the prediction is de-tokenized.
series = np.random.rand(101)
input = series[:-1]
target = series[1:] # shifted by 1
input_ids, p = tokenizer.encode(input)
target_ids = tokenizer.encode(enc, p)
predict_ids = model.generate(input_ids, max_new_tokens=20)
predictions = tokenizer.decode(predict_ids, p)
Using mostly everything as described in the last section, except changed the causalLM model here, and did not use the Target Tokenization scheme described above.
Instead, a sequence of length max_seq_len was normalized using its own statistics, and digitized to get the input_ids.
Using LlamaForCausalLM implementation from HF.
model_config = {
"vocab_size": None,
"hidden_size": 256,
"intermediate_size": 512,
"num_hidden_layers": 4,
"num_attention_heads": 4,
"max_position_embeddings": None
}
The dataset used was 414 hourly time-series from the M4 dataset. The minimum and maximum number of observations in the time-series were 700~900, excluding the test observations.
m4_trainer.py is the training script for this experiment.
The m4_evaluator.py script can be used to generate the test plots and report the sMAPE and MASE numbers for this dataset.
A small sample of forecasts/generations on the test set of the M4 hourly dataset is shown here:
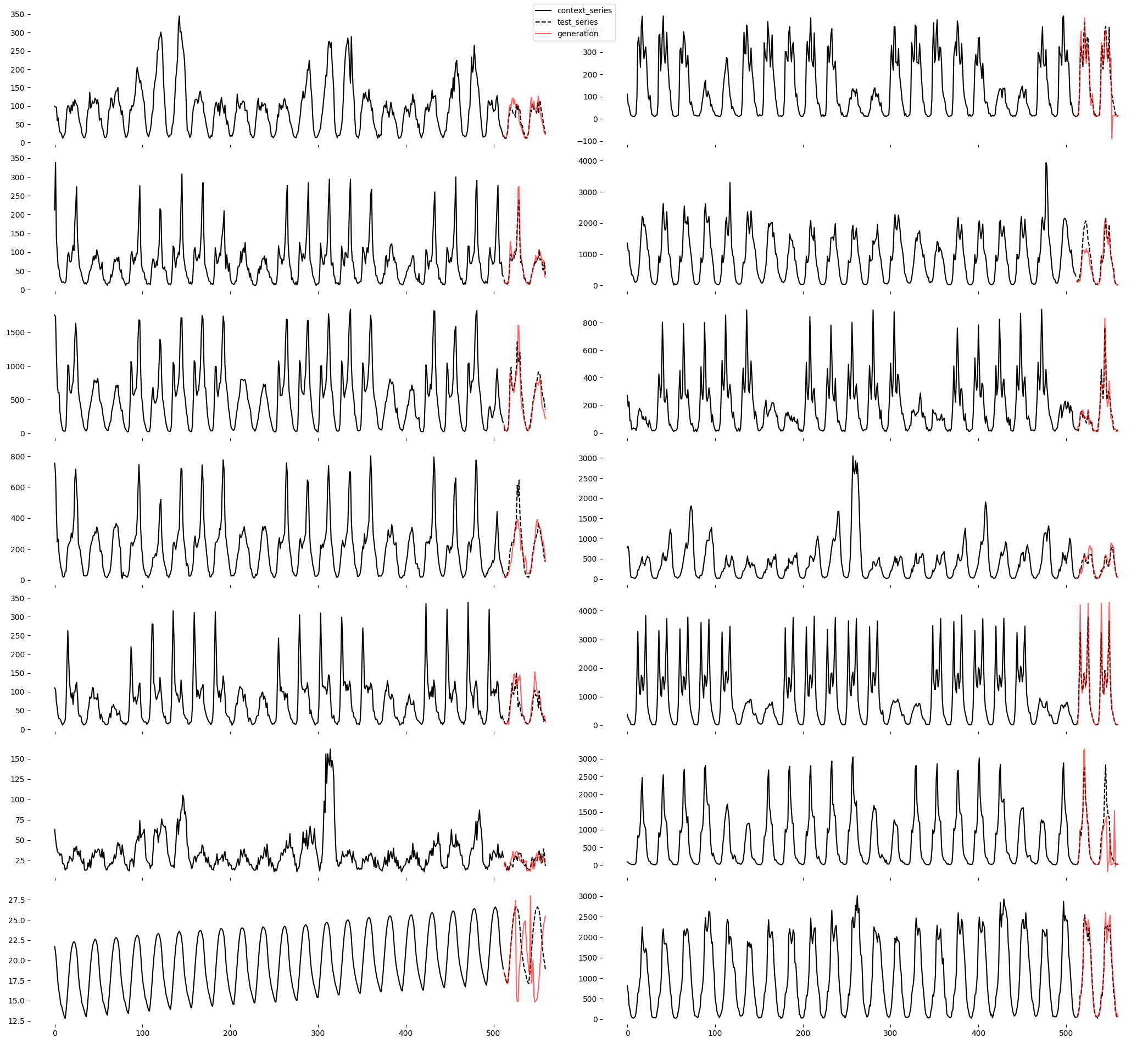
Using vanilla GPT-2 model and trainer from Andrej Karparthy's nanoGPT repo, with the introduced time-series tokenization scheme that converts time-series into sequences of tokens. These tokens are then fed into the GPT model as input during training. The model is trained to predict the next token in the sequence, which is then decoded back into its corresponding time-series value. This experiment was used to test the feasibility of this tokenization scheme
Some forecasting results can be found in output/. The results are from a 6.5M parameters model trained on ~3000 timeseries with a total of ~3M timestamps for 1000 iterations with the following configuration:
model.n_embd = 128
model.n_head = 8
model.block_size = 256
model.n_layer = 8
model.dropout = 0.05