Purely Functional, Real-Time Deques with Catenation [284ko postscript]
by Haim Kaplan and Robert E. Tarjan
journal of the ACM 31:11-16 (1999) 1709-1723 https://doi.org/10.1145/324133.324139
Following the paper, this library provides 4 implementations of double-ended queues which let you push, pop and append elements at both ends of an ordered collection in worst-case constant time (strict! not amortized) :
| Module | cons | uncons | snoc | unsnoc | append | rev | nth |
|---|---|---|---|---|---|---|---|
| Dequeue | O(1) | O(1) | O(1) | O(1) | 🚫 | O(1) | O(log min(i, N-i)) |
| Steque | O(1) | O(1) | O(1) | 🚫 | O(1) | 🚫 | 🚫 |
| Deck | O(1) | O(1) | O(1) | O(1) | O(1) | 🚫 | 🚫 |
| Deckrev | O(1) | O(1) | O(1) | O(1) | O(1) | O(1) | 🚫 |
Check out the online documentation for the full interface -- which should be mostly compatible with OCaml's standard List module.
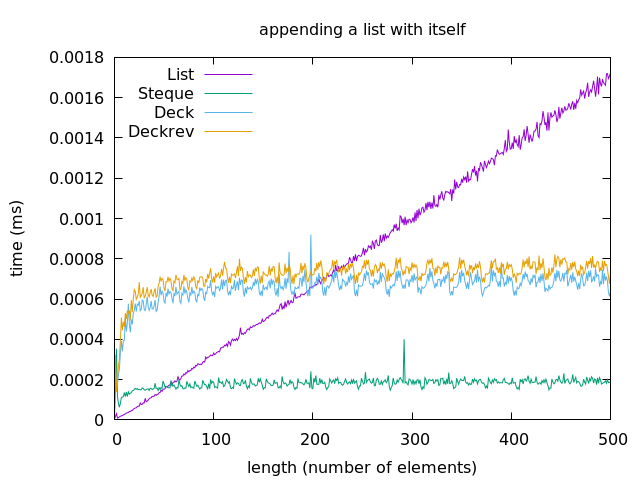
Even though the algorithmic complexity is great, these deques add a significant overhead when compared to lists:
| List | Dequeue | Steque | Deck | Deckrev | |
|---|---|---|---|---|---|
cons |
1x | 1.5x | 1.6x | 1.6x | 2.5x |
uncons |
1x | 13x | 13x | 19x | 22x |
fold_left |
1x | 4.5x | 4.5x | 4.5x | 11.1x |
Example applications include:
- ngrams.ml uses a sliding window to enumerate the ngrams of a string.
- knuth_plass.ml implements the optimal line breaking algorithm of Knuth & Plass (of TeX fame) as described by Oege de Moor and Jeremy Gibbons in Bridging the algorithm gap: A linear-time functional program for paragraph formatting.
- string_builder.ml shows how to improve the asymptotics of a monoidal "concat" operator, a common design pattern in purely functional libraries. Surprisingly, this benchmark reveals that the simpler difference lists may exhibit weird edge cases in addition to being less flexible. See Reflection without remorse by Atze van der Ploeg and Oleg Kiselyov for a non-obvious application to monadic computations.
- zipper.ml is a classic zipper to iterate over an
ordered collection, with the added benefit that one can instantly close the
traversal in
O(1)rather thanO(length traversed). Such a zipper is a prerequisite for Brodal's Fast Join-trees and the Functional Link-Cut trees of Erik Demaine. - Finally, these deques are suitable for marshalling and serialization as they do not use lazy or functional values in their spine.
None of this code would have been possible without the fantastic support for GADTs in OCaml. The invariants are encoded inside each datatypes: the algorithms then follow, guided by the type checker and the lack of recursion. As this does not result in the most readable code, you should read the paper if you want to understand the big ideas:
- Skewed number systems to deamortize carry propagation
- Recursive slowdown and bootstrapping
- Datastructures with a hole / with a preferred path to define
O(1)fingers inside a purely functional tree
The core types and algorithms described in the paper can be found in the
src/*_internal.ml files.