artificial-scientist-lab/Impact4Cast

Forecasting high-impact research topics via machine learning on evolving knowledge graphs

Forecasting high-impact research topics via machine learning on evolving knowledge graphs

Authors: Xuemei Gu, Mario Krenn
Preprint: arXiv:2402.08640

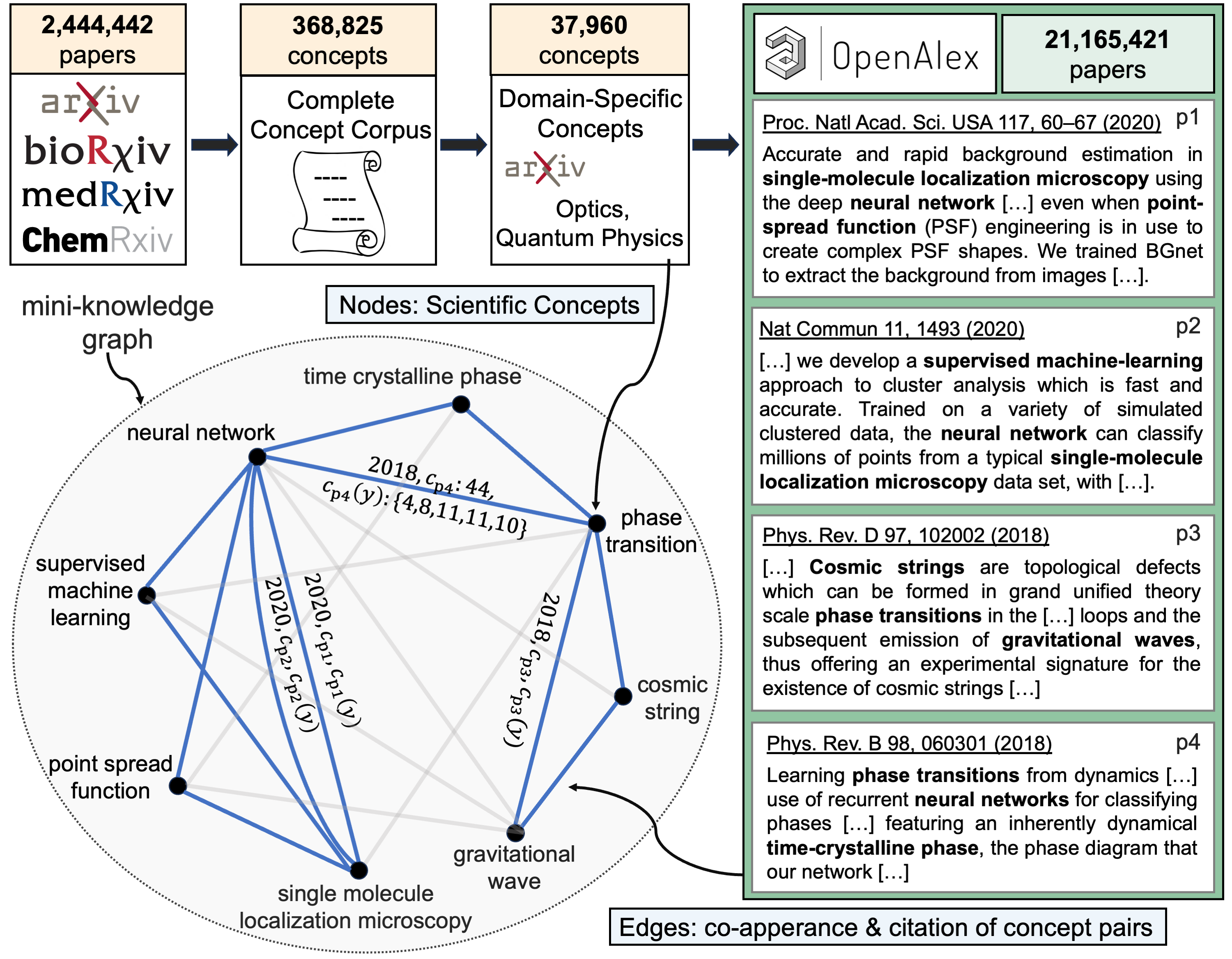
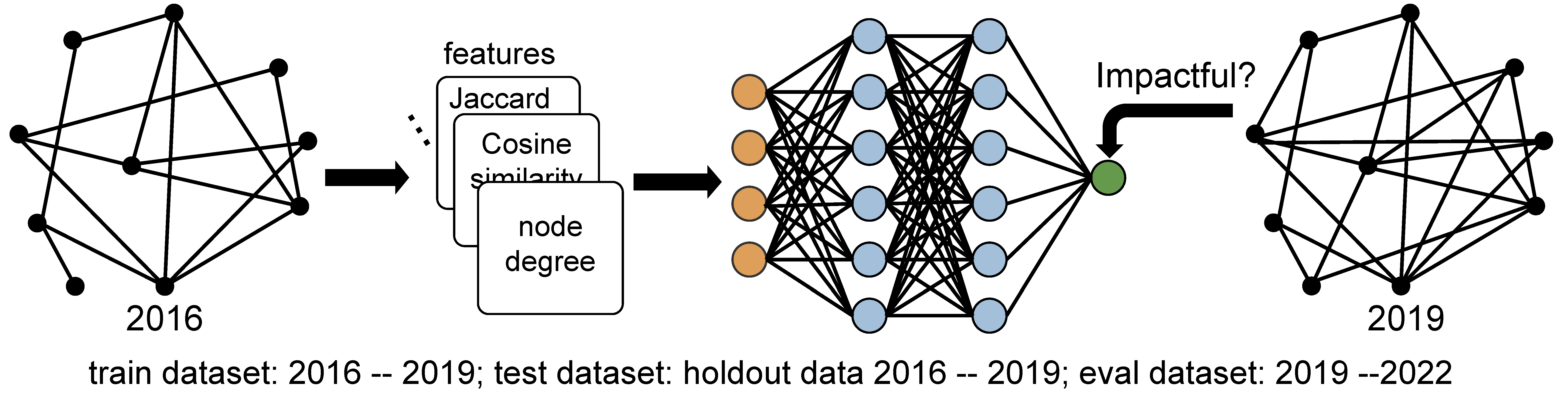
Which scientific concepts, that have never been investigated jointly, will lead to the most impactful research?

Note

Full Dynamic Knowledge Graph and Datasets can be downloaded via zenodo.org

Prepare an evolving, citation-augmented knowledge graph

Creating a list of scientific concepts

create_concept
│ 
├── Concept_Corpus
│   ├── s0_get_preprint_metadata.ipynb: Get metadata from chemRxiv, medRxiv, bioRxiv (arXiv data from Kaggle)
│   ├── s1_make_metadate_arxivstyle.ipynb: Preprocessing metadata from different sources
│   ├── s2_combine_all_preprint_metadate.ipynb: Combining metadata
│   ├── s3_get_concepts.ipynb: Use NLP techniques (for instance RAKE) to extract concepts
│   └── s4_improve_concept.ipynb: Further improvements of full concept list
│   
└── Domain_Concept
    ├── s0_prepare_optics_quantum_data.ipynb: Get papers for specific domain (optics and quantum physics in our case).
    ├── s1_split_domain_papers.py: Prepare data for parallelization.
    ├── s2_get_domain_concepts.py: Get domain-specific vertices in full concept list.
    ├── s3_merge_concepts.py: Postprocessing domain-specific concepts
    ├── s4_improve_concepts.ipynb: Further improve concept lists
    ├── s5_improve_manually_concepts.py: Manually inspect the concepts in the very end for grammar, non-conceptual phrases, verbs, ordinal numbers, conjunctions, adverbials and so on, to improve quality
    └── full_domain_concepts.txt: Final list of 37,960 concepts (represent vertices of knowledge graph)

Creating dynamic knowlegde graph

create_dynamic_edges
├── _get_openalex_workdata.py: Get metadata from OpenAlex)
├── _get_openalex_workdata_parallel_run1.py: Get parts of the metadata from OpenAlex (run in many parts)
├── get_concept_pairs.py: Create edges of the knowledge graph (edges carry the time and citation information).
├── merge_concept_pairs.py: Combining edges files
└── process_edge_to_pandas_frame.py: Post-processing, store the full dynamic knowledge graph

Prepare other data

.
├── prepare_unconnected_pair_solution.ipynb: Find unconnected concept pairs (for training, testing and evaluating)
├── prepare_adjacency_pagerank.py: Prepare dynamic knowledge graph and compute properties
├── prepare_node_pair_citation_data_years.ipynb: Prepare citation data for both individual concept nodes and concept pairs for specific years
│
├──create_dynamic_concepts
│  ├── get_concept_citation.py: Create dynamic concepts from the knowledge graph (concepts carry the time and citation information). 
│  ├── merge_concept_citation.py: Combining dynamic concepts files
│  └── process_concept_to_pandas_frame.py: Post-processing, store the full dynamic concepts
│  ├── merge_concept_pairs.py: Combining dynamic concepts
│  └── process_edge_to_pandas_frame.py: Post-processing, store the full dynamic concepts
│
└──prepare_eval_data
   ├── prepare_eval_feature_data.py: Prepare features of knowledge graph (for evaluation dataset)
   └── prepare_eval_feature_data_condition.py: Prepare features of knowledge graph (for evaluation dataset, conditioned on existence in the future)

🤖Forecasting with Neural Network

.
├── train_model_2019_run.py: Training neural network from 2016 -> 2019 (evaluated form 2019 -> 2022).
├── train_model_2019_condition.py: Training neural network from 2016 -> 2019 (evaluated form 2019 -> 2022, conditioned on existence in the future)
├── train_model_2019_individual_feature.py: Training neural network from 2016 -> 2019 (evaluated form 2019 -> 2022) on individual features
└── train_model_2022_run.py: Training 2019 -> 2022 (for real future predictions of 2025)

Feature descriptions for an unconnected pair of concepts (u, v)

Feature Type	Feature Index	Feature Description
node feature	0-5	the number of neighbours for vertices $u$ and $v$ in years $y$, $y-1$, $y-2$ denoted as: $N_{u,y}$, $N_{v,y}$, $N_{u,y-1}$, $N_{v,y-1}$, $N_{u, y-2}$, $N_{v, y-2}$
	6-7	the number of new neighbors since 1 years prior to $y$ for vertices $u$ and $v$ denoted as: $N_{u,y}^{\Delta}$, $N_{v,y}^{\Delta}$
	8-9	the number of new neighbors since 2 years prior to $y$ for vertices $u$ and $v$ denoted as: $N_{u,y}^{\Delta 2}$, $N_{v,y}^{\Delta 2}$
	10-11	the rank of the number of new neighbors since 1 years prior to $y$ for vertices $u$ and $v$ denoted as: $rN_{u,y}^{\Delta}$, $rN_{v,y}^{\Delta}$
	12-13	the rank of the number of new neighbors since 2 years prior to $y$ for vertices $u$ and $v$ denoted as: $rN_{u,y}^{\Delta 2}$, $rN_{v,y}^{\Delta 2}$
	14-19	the PageRank score for vertices $u$ and $v$ in years $y$, $y-1$, $y-2$ denoted as: $PR_{u,y}$, $PR_{v,y}$, $PR_{u,y-1}$, $PR_{v,y-1}$, $PR_{u, y-2}$, $PR_{v, y-2}$
node citation feature	20-25	yearly citation for vertices $u$ and $v$ during the years $y$, $y-1$, $y-2$ denoted as: $c_{u,y}$ , $c_{v,y}$, $c_{u,y-1}$, $c_{v,y-1}$, $c_{u,y-2}$, $c_{v,y-2}$
	26-31	total citation for vertices $u$ and $v$ since their first publications to the year $y$, $y-1$, $y-2$ denoted as: $ct_{u,y}$ , $ct_{v,y}$, $ct_{u,y-1}$, $ct_{v,y-1}$, $ct_{u,y-2}$, $ct_{v,y-2}$
	32-37	total citation for vertices $u$ and $v$ in three-year period ending with the year $y$, $y-1$, $y-2$ denoted as: $ct^{\Delta 3}_{u,y}$ , $ct^{\Delta 3}_{v,y}$, $ct^{\Delta 3}_{u,y-1}$, $ct^{\Delta 3}_{v,y-1}$, $ct^{\Delta 3}_{u,y-2}$, $ct^{\Delta 3}_{v,y-2}$
	38-43	the number of papers mentioning either concept ($u$ or $v$) until the year $y$, $y-1$, $y-2$ denoted as: $pn_{u,y}$ , $pn_{v,y}$, $pn_{u,y-1}$, $pn_{v,y-1}$, $pn_{u,y-2}$, $pn_{v,y-2}$
	44-49	The average yearly citation for vertices $u$ and $v$ during the years $y$, $y-1$, and $y-2$ calculated based on the total citations received during the year divided by the number of papers mentioning the vertices from their first publications up to the respective year denoted as: $cm_{u,y}$ , $cm_{v,y}$, $cm_{u,y-1}$, $cm_{v,y-1}$, $cm_{u,y-2}$, $cm_{v,y-2}$; as an example: $cm_{u,y}$ is $\frac{c_{u,y}}{pn_{u,y}}$
	50-55	The average total citation for vertices $u$ and $v$ since their first publications to the year $y$, $y-1$, $y-2$ determined by dividing the cumulative citations by the count of papers that mentioned these vertices since their first publications denoted as: $ctm_{u,y}$ , $ctm_{v,y}$, $ctm_{u,y-1}$, $ctm_{v,y-1}$, $ctm_{u,y-2}$, $ctm_{v,y-2}$; as an example: $ctm_{u,y}$ is $\frac{ct_{u,y}}{pn_{u,y}}$
	56-61	The average total citation for vertices $u$ and $v$ in three-year period ending with the year $y$, $y-1$, $y-2$ calculated by dividing the cumulative three-year period citations by the count of papers that mentioned these vertices since their first publications denoted as: $ctm^{\Delta 3}_{u,y}$ , $ctm^{\Delta 3}_{v,y}$, $ctm^{\Delta 3}_{u,y-1}$, $ctm^{\Delta 3}_{v,y-1}$, $ctm^{\Delta 3}_{u,y-2}$, $ctm^{\Delta 3}_{v,y-2}$; as an example: $ctm^{\Delta 3}_{u,y}$ is $\frac{ct^{\Delta 3}_{u,y}}{pn_{u,y}}$
	62-63	the number of new citations for vertices $u$ and $v$, since 1 years prior to y denoted as: $cnew^{\Delta 1}_{u,y}$ , $cnew^{\Delta 1}_{v,y}$
	64-65	the number of new citations for vertices $u$ and $v$, since 2 years prior to y denoted as: $cnew^{\Delta 2}_{u,y}$ , $cnew^{\Delta 2}_{v,y}$
	66-67	the rank of the number of new citations for vertices $u$ and $v$, since 1 year prior to y denoted as: $rcnew^{\Delta 1}_{u,y}$ , $rcnew^{\Delta 1}_{v,y}$
	68-69	the rank of the number of new citations for vertices $u$ and $v$, since 2 years prior to y denoted as: $rcnew^{\Delta 2}_{u,y}$ , $rcnew^{\Delta 2}_{v,y}$
	70-71	the number of new papers mentioning vertices $u$ and $v$, since 1 year prior to y denoted as: $pnew^{\Delta 1}_{u,y}$ , $pnew^{\Delta 1}_{v,y}$
	72-73	the number of new papers mentioning vertices $u$ and $v$, since 2 years prior to y denoted as: $pnew^{\Delta 2}_{u,y}$ , $pnew^{\Delta 2}_{v,y}$
	74-75	the rank of the number of new papers mentioning vertices $u$ and $v$, since 1 year prior to y denoted as: $rpnew^{\Delta 1}_{u,y}$ , $rpnew^{\Delta 1}_{v,y}$
	76-77	the rank of the number of new papers mentioning vertices $u$ and $v$, since 2 years prior to y denoted as: $rpnew^{\Delta 2}_{u,y}$, $rpnew^{\Delta 2}_{v,y}$
pair feature	78-80	the number of shared neighbors between vertices $u$ and $v$ for the years $y$, $y-1$, $y-2$ denoted as: $ns_{y}$, $ns_{y-1}$, $ns_{y-2}$
	81-83	the geometric coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by number_shared_neighbor**2 / (deg_u * deg_v), deg_u is the degree of vertex $u$ denoted as: $geo_{y}$, $geo_{y-1}$, $geo_{y-2}$
	84-86	the cosine coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by geometric_index**0.5 denoted as: $cos_{y}$, $cos_{y-1}$, $cos_{y-2}$
	87-89	the simpson coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by number_shared_neighbor / np.min([deg_u, deg_u]) denoted as: $spi_{y}$, $spi_{y-1}$, $spi_{y-2}$
	90-92	the preferential attachment coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by deg_u*deg_u denoted as: $pre_{y}$, $pre_{y-1}$, $pre_{y-2}$
	93-95	the Sørensen–Dice coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by 2*num_shared_neighbor / (deg_u + deg_v) denoted as: $sod_{y}$, $sod_{y-1}$, $sod_{y-2}$
	96-98	the jaccard coefficient for the pair ($u$ and $v$) for the years $y$, $y-1$, $y-2$ calculated by num_shared_neighbor/(deg_u + deg_v - num_shared_neighbor) denoted as: $jac_{y}$, $jac_{y-1}$, $jac_{y-2}$
pair citation feature	99-101	the ratio of the sum of citations received by concepts $u$ and $v$ in the year $y$ to the sum of number of papers mentioning either concept, similar for years $y-1$, $y-2$ calculated by ($c_{u,y}$ + $c_{v,y}$) / ($pn_{u,y}$ + $pn_{v,y}$)
	102-104	the ratio of the product of citations received by concepts $u$ and $v$ in the year $y$ to the sum of number of papers mentioning either concept, similar for years $y-1$, $y-2$ calculated by ($c_{u,y}$ * $c_{v,y}$) / ($pn_{u,y}$ + $pn_{v,y}$)
	105-107	the sum of the average citations received by concepts $u$ and $v$ in the year $y$, $y-1$, $y-2$ e.g., calculated by ($cm_{u,y}$ + $cm_{v,y}$) for year y
	108-110	the sum of the average total citations received by concepts $u$ and $v$ from their first publication up to the year $y$, $y-1$, $y-2$ e.g., calculated by ($ctm_{u,y}$ , $ctm_{v,y}$) for year y
	111-113	the sum of the citations received by concepts $u$ and $v$ in the three-year period ending with year $y$, $y-1$, $y-2$, e.g., calculated by ($ct^{\Delta 3}_{u,y}$ + $ct^{\Delta 3}_{v,y}$) for year y
	114-116	the sum of the average citations received by concepts $u$ and $v$ in the three-year period ending with year $y$, $y-1$, $y-2$, e.g., calculated by ($ctm^{\Delta 3}_{u,y}$ + $ctm^{\Delta 3}_{v,y}$) for year y
	117-119	the minimum number of the citations received by either concept $u$ or $v$ in the year $y$, $y-1$, $y-2$, e.g., min($c_{u,y}$, $c_{u,y}$)
	120-122	the maximum number of the citations received by either concept $u$ or $v$ in the year $y$, $y-1$, $y-2$, e.g., max($c_{u,y}$, $c_{u,y}$)
	123-125	the minimum number of the total citations received by either concept $u$ or $v$ since its frist publication to the year $y$, $y-1$, $y-2$, e.g., min($ct_{u,y}$, $ct_{u,y}$)
	126-128	the maximum number of the total citations received by either concept $u$ or $v$ since its frist publication to the year $y$, $y-1$, $y-2$, e.g., max($ct_{u,y}$, $ct_{u,y}$)
	129-131	the minimum number of total citations received by either concept $u$ or $v$ in the three-year period ending with year $y$, $y-1$, $y-2$, e.g., min($ct^{\Delta 3}_{u,y}$ , $ct^{\Delta 3}_{v,y}$)
	132-134	the maximum number of total citations received by either concept $u$ or $v$ in the three-year period ending with year $y$, $y-1$, $y-2$, e.g., max($ct^{\Delta 3}_{u,y}$ , $ct^{\Delta 3}_{v,y}$)
	135-137	the minimum number of papers mentioning either concept $u$ or $v$, for year $y$, $y-1$, $y-2$; e.g., min($pn_{u,y}$ , $pn_{v,y}$), min($pn_{u,y-1}$ , $pn_{v,y-1}$), min($pn_{u,y-2}$ , $pn_{v,y-2}$)
	138-140	the maximum number of papers mentioning either concept $u$ or $v$, for year $y$, $y-1$, $y-2$; e.g., max($pn_{u,y}$ , $pn_{v,y}$), max($pn_{u,y-1}$ , $pn_{v,y-1}$), max($pn_{u,y-2}$ , $pn_{v,y-2}$)