/stable-marriage-problem

Repo to simulate the Stable Marriage Problem

Primary LanguagePython

Stable Marriage Problem

This repo attempts to implement the classic algorithm to the Stable Marriage Problem and other variants.

More information can be found on my blog post.

File Structure

  • /classic
    • stable_marriage_problem_classic.py
      • This file implements a Community object which represents the actors and algorithm in the SMP
      • In root directory, run: python3 -m classic.stable_marriage_problem_classic
    • simulations.py
      • This is the file to execute in order to run some simulations of the algorithm
      • Adjust the values in main() to tweak executions of the simulation
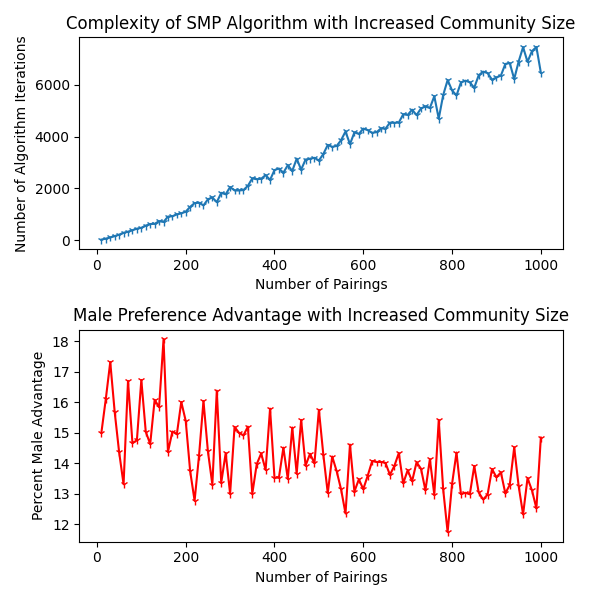
      • In root directory, run: python3 -m classic.simulations
        • Executing the code as is should produce the following graph:

  • /distribution
    • stable_marriage_problem_distribution.py
      • This file implements a Community object which represents the actors and algorithm in the SMP, but applies a normal/pareto asymmetry in preferences between men/women
      • In root directory, run: python3 -m distribution.stable_marriage_problem_distribution
    • simulations.py
      • This is the file to execute in order to run some simulations of the algorithm
      • Adjust the values in main() to tweak executions of the simulation
      • This is pretty much the same code as the simulations.py in the /classic package
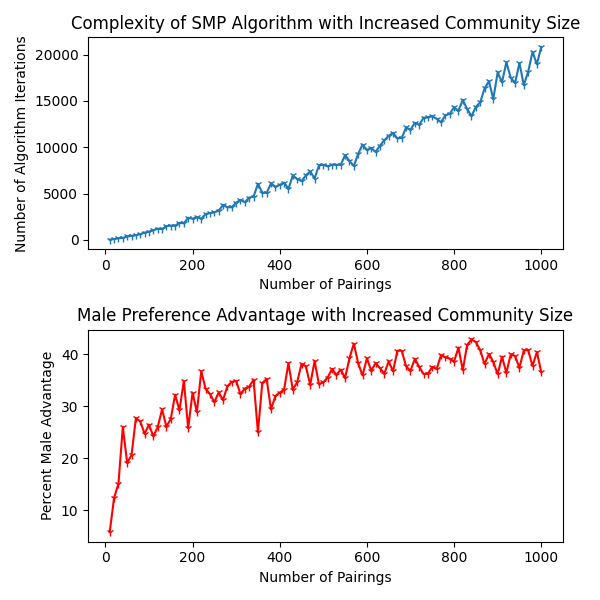
      • In root directory, run: python3 -m distribution.simulations
        • Executing the code as is should produce the following graph:

Future Considerations

  • Different distributions and analyzing the asymmetry

    • Currently only the normal/pareto distributions were analyzed
    • How would advantage be affected with different distribution parameters (e.g. Different alpha values for pareto)
    • How would advantage be affected with different distributions entirely (e.g. Poisson)

  • "Subgroup" preference

    • As a community grows larger, there are usually smaller subgroups formed (e.g. neighborhoods in Manhattan)
    • With this in mind, we can tweak the preference lists to favor proposals within one's subgroup, even if there are more "attractive" people in another subgroup
    • Subgroups would most probably be formed by analyzing the distribution of subgroup populations