MatrixAnalysis101

The goal of MatrixAnalysis101 is to … Run some elementary matrix algebra proprieties

Installation

Você pode fazer o download do pacote no R usando:

if(!require(devtools)) install.packages("devtools")
devtools::install_github("arzevedo/MatrixAnalysis101")

library(MatrixAnalysis101)

[G = (A + C B D)]

Processo de aprendizado e Objetivos faltantes

Lista de coisas que eu precisei aprender ou revisitar para chegar até onde cheguei.

✔️ Relembrar conceitos operações básicas com matrizes
✔️ Relembrar Propriedades da matrix inversa e seu caracter exclusivo
✔️ Operações com matrizes em blocos
✔️ Encontrar (A), (B), (C) e (D)
✔️ Complemento de Schur
✔️ *Encontrar a inversa da matrizes densas de uma maneira mais eficiente do que tirar a inversa na mão

O teorema 1.9 de Schott [1]

Sejam (A_{mxm}) e (B_{nxn}) matrizes não singulares ((det(A) \neq 0) e (det(B) \neq 0)). Para qualquer matriz (C_{mxn}) e qualquer matriz (D_{nxm}), vale que (A + CBD) é não singular, então [G^{-1} = (A + CBD)^{-1} = A^{-1} - A^{-1}C(B^{-1}+DA^{-1}C)^{-1} DA^{-1}]

Na mesma aula em que passou a atividade Kim deu a dica de que (A) ou (B) deveriam ser a matrix identidade com a dimensão pertinente a matrix (G), para comportar a dimensão na igualdade (G = A + CBD).

A busca por (CBD)

Intuitivamente, meu ponto de partida foi ir atrás de (A), (B), (C) e (D). Com a dica do Kim (A = I_{m}) foquei em ir atrás do resultado (G - A = CBD) e após assitir alguns videos de Gilbert Strang para relembrar conceitos fundamentais de factorização, autovalores, autovetores e decomposição espectral (Acabei vendo os videos sobre SVD que eu não havia visto em algebra linear!)

Funcionamento das funções

A função theorem_1_9 executa todos os passos expostos acima

theorem_1_9 <- function(W, extra_output = FALSE){
  
  if(det(W) == 0) stop("\nErro!\nA matriz input é singular !\nNão faça isso!\nReveja seus conceitos")
  Inde <- diag(nrow(W))
  #Quantas linhas são Linearmente independentes ----
  reduc_depen <- pracma::rref(W - Inde)
  n_depen <- dim(reduc_depen[rowSums(reduc_depen),])[1]
  
  # SVD ----
  S_svd <- svd(W - Inde,
               # Ja que a matriz e quadrada:
               nu = n_depen, nv = n_depen)
  S_sig <- diag(S_svd$d)
  S_sig_f <- S_sig[rowSums(S_sig) > 1e-10, colSums(S_sig) > 1e-10]
  S_v <- S_svd$v
  S_u <- S_svd$u
  
  S_svd_output <- zapsmall(S_u %*% S_sig_f %*% t(S_v))
  
  out_inverse <- (Inde - Inde %*% S_u %*% solve(solve(S_sig_f)+ t(S_v) %*% Inde %*% S_u) %*% t(S_v) %*% Inde)
  
  out_inverse <- zapsmall(out_inverse)
  
  if(extra_output == TRUE){
    out <- out <- list(sua_matriz = W,
                       suas_ABCD = list(
                         A = diag(nrow(W)),
                         B = S_sig_f,
                         C = S_u,
                         D = t(S_v)
                       ),
                       sua_inversa = out_inverse
                       )
  
  } else {
      out <- out_inverse
    }
  
  return(out)
  
}

Caso queira visualizar o resultado das matrizes (A), (B), (C) e (D) coloque extra_output = TRUE.

Opção ao teorema 1.9

Não fiquei satisfeito com o resultado da função do Teorema 1.9. 1º porque não consegui obter os valores iguas ao do livro e 2º porque não senti tanta praticidade assim, o processo me parece mais custoso do que simplesmente aplicar afunção solve na matriz.

schur_inv <- function(A, extra_output = FALSE){

  if(det(A) == 0) stop("\nErro!\nA matriz input é singular !\nNão faça isso!\nReveja seus conceitos")
  
  n_row <- dim(A)[1]
  n_col <- dim(A)[2]
  th <- ifelse(dim(A)[1]%/%2, 2, 3)
  
  E_m <- A[1:(n_row - th), 1:(n_col - th)]
  F_m <- A[1:(n_row - th), (n_col - th + 1):n_col]
  P_m <- A[(n_row - th + 1):n_row, 1:(n_col - th)]
  H_m <- A[(n_row - th + 1):n_row, (n_col - th + 1):n_col]
  
  H_1 <- solve(H_m)
  E_1 <- solve(E_m)
  
  S <- H_m - (P_m %*% E_1 %*% F_m)
  S_1 <- solve(S)
  T_m <- E_m - (F_m %*% H_1 %*% P_m)
  T_m_1 <- solve(T_m)
  
  
  A_1 <- matrix(0, ncol = n_col, nrow = n_row)
  A_1[1:(n_row - th), 1:(n_col - th)] <- T_m_1
  A_1[1:(n_row - th), (n_col - th + 1):n_col] <- - E_1 %*% F_m %*% S_1
  A_1[(n_row - th + 1):n_row, 1:(n_col - th)] <- - H_1 %*% P_m %*% T_m_1
  A_1[(n_row - th + 1):n_row, (n_col - th + 1):n_col] <- S_1
  
  
  if(extra_output == TRUE){
    out <- list(
      sua_matriz = A,
      suas_ABCD = list(
        T_m_1 = T_m_1,
        A_12 = - E_1 %*% F_m %*% S_1,
        A21 = - H_1 %*% P_m %*% T_m_1,
        S_1 = S_1
        ),
      sua_inversa = A_1
      )
  } else {
      out <- A_1
    }

  return(out)
}

Conclusões

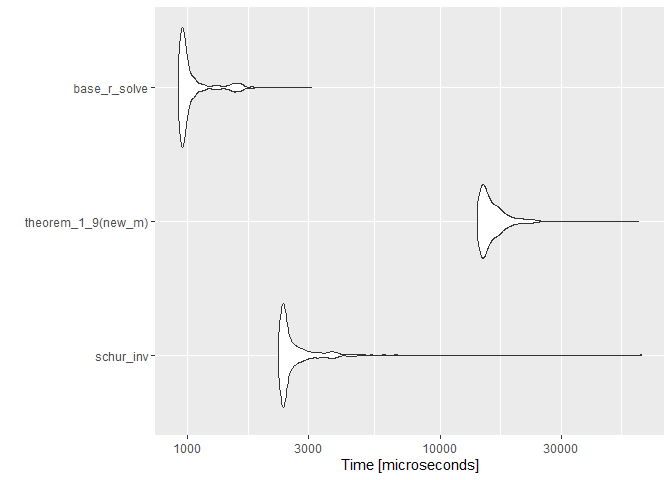
Como eu achei muito mais tranquilo entender a inversa usando o metodo de partições de Schur, acabei tomando a liberdade de testar a performance das duas funções para ver qual é a mais eficiente.

all.equal(
  schur_inv(new_m),
  solve(new_m)
)
#> [1] TRUE
all.equal(
  theorem_1_9(new_m),
  solve(new_m)
)
#> [1] "Mean relative difference: 3.384245e-07"
all.equal(
  theorem_1_9(new_m),
  schur_inv(new_m)
)
#> [1] "Mean relative difference: 3.384245e-07"

Fontes

James R. Schott (2017) Matrix Analysis for Statistics