Finite difference discretization scheme for diffusion in a sphere with variable diffusivity
This code solves the PDE for Fickian diffusion with variable diffusivity within a radially symmetric sphere. The PDE is solved numerically using method of lines, the spherical finite difference discretization scheme defined and analyzed in the reference, and any built-in MATLAB ODE solver. Examples are provided for variable diffusivity cases I-IV presented in the reference listed below. The use of ode45 solver is shown in this code. Any ODE solver could be selected.
Ashlee N. Ford Versypt, School of Chemical Engineering, Oklahoma State University ashleefv@okstate.edu
When using this software, please cite:
A. N. Ford Versypt & R. D. Braatz, Analysis of finite difference discretization schemes for diffusion in spheres with variable diffusivity, Computers & Chemical Engineering, 71 (2014) 241-252, https://doi.org/10.1016/j.compchemeng.2014.05.022
DCASE = 1; Case I: constant diffusivity with alpha = alpha0
DCASE = 2; Case II: time-dependent diffusivity alpha = alpha0 for t =< tau and alpha = alpha0exp(k(t - tau)) for t > tau
DCASE = 3; Case III: spatially dependent diffusivity alpha = alpha0*r^2
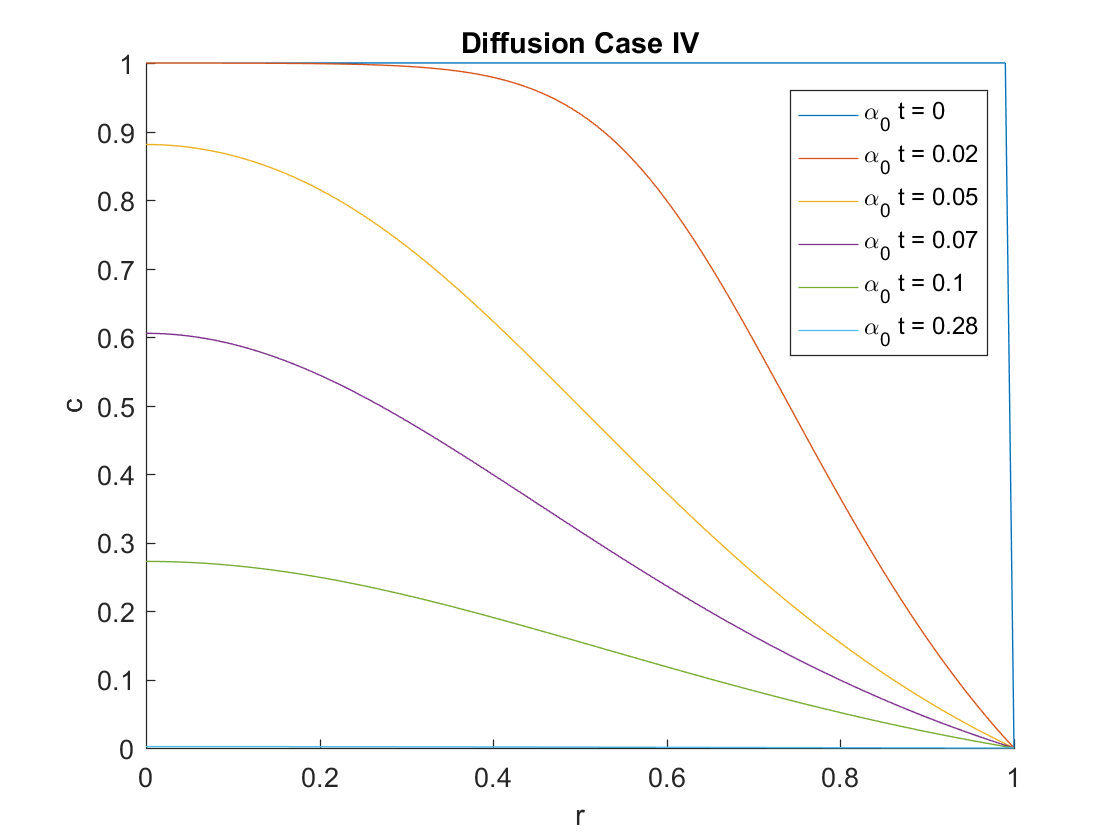
DCASE = 4; CASE IV: concentration-dependent diffusivity alpha = alpha0exp(k-kc)
solve_FD_spheres_variable_diffusivity.m solves the diffusion PDE in spherical coordinates for c(r,t) with variable diffusivity defined by DCASE
FD_spheres_variable_diffusivity uses the finite difference discretization scheme defined in the reference as Scheme 1 and the variable diffusivity Cases I-IV analyzed in that work.