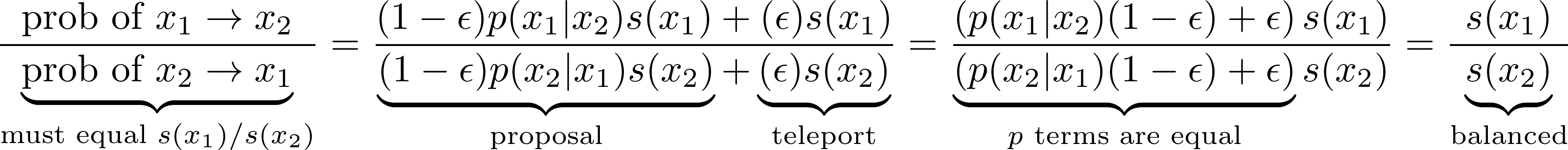Laith Alhussein, Nathaniel Burbank, Shawn Pan, Andrew Ross, and Rohan Thavarajah
We've moved our project website! It's now at http://teleporting-parallel-mcmc.s3-website-us-east-1.amazonaws.com.
The rest of this is now old, but you can still read if you like:
Markov Chain Monte Carlo (MCMC) is a statistical method that allows us to draw samples from complicated probability distributions for which we can only calculate relative likelihoods between locations. It operates by starting at a particular location on the distribution, proposing a next location, and making a random decision to move or stay put based on that relative likelihood. After many iterations of this process, the resulting "trace" of locations converges to samples from the distribution of interest -- if the process by which the algorithm proposes and chooses points satisfies a condition known as detailed balance.
MCMC is a major enabler of "big science"; beyond pure statistics, many important simulations in physics, chemistry, and even weather forecasting [cite] involve taking samples or averages (computed from samples) of distributions intractable to direct integration.
However, MCMC suffers from a major problem when it comes to multimodal distributions. These are cases in which there exist multiple disjoint outcome regions that are each equally likely. In particular, the local stepping method which lets MCMC algorithms handle intractable distributions is exactly what hampers it from multimodal sampling; to move from one mode to another, the chain must bridge a chasm of very low probability density, which is unlikely. In these cases, the MCMC chain frequently gets “stuck” in one of the modes and fails to converge. The results from a trace generated under these circumstances are biased and no longer representative of the distribution we were attempting to sample from.
In theory, even with a multimodal distribution a chain run for an infinite number of iterations will eventually explore all of the modes if we use a proposal distribution whose support is infinite. Additionally, running parallel chains may also help, as would more high-powered proposal methods like Hamiltonian Monte-Carlo (HMC), which introduces the concept of momentum to allow the chain to more efficiently explore its space. In practice however, even with many chains run in parallel for many iterations, we still may not solve the problem efficiently.
For a distribution we know beforehand, there are a variety of convergence
metrics we can apply (which we will detail later). We can analyze the extent to
which parallelism helps us converge faster in the framework of parallel
computing. In particular, for a given MCMC algorithm and a given distribution,
we can define T₁ as the number of iterations required to converge for a
single chain, and T∞ as the number of iterations required to converge if we
combine results from an infinite number of parallel chains. For many
distributions, there is some "burnin" B, which is the number of samples we
need to discard from the beginning of the chain that are unrepresentative,
since they depend on the arbitrary location where we start (not on the
distribution itself). In this case, we actually have T∞ = B+1, since we can
take one sample from infinitely many chains after burnin.
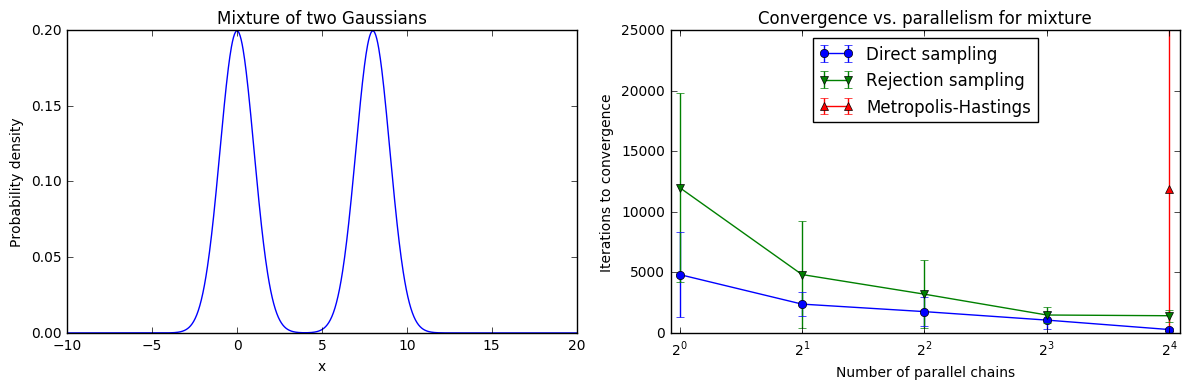
Following this analysis, we can plot speedup, efficiency, and cost graphs for a number of sampling algorithms on a number of different distributions. For example, here is a comparison of how the convergence time of three sampling methods on a simple, 1D Gaussian mixture varies with the degree of parallelism of the sampler:
where we defined "convergence time" as the number of iterations until the sample mean stayed within 0.05 of the true mean for a large number of iterations.
Note that direct sampling is the most reliable and fastest to converge, while rejection sampling is less efficient and has higher variance (since it must reject a large percentage of the samples it draws). Metropolis-Hastings, the classic MCMC algorithm, fails to converge entirely even with 50,000 iterations per chain until we concatenate together 16 parallel chains because it cannot handle even basic multimodality efficiently.
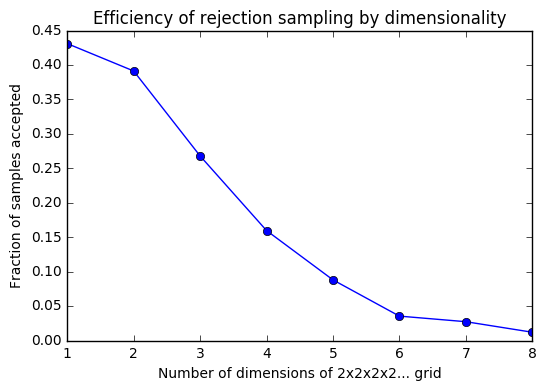
However, in general, direct sampling isn't usually possible for problems we care about, and the efficiency of rejection sampling drops exponentially as we increase the number of dimensions:
So we generally must use local sampling techniques. But rather than trying to speed up their convergence by adding more parallel machines running the same unsuitable algorithm, we can parallelize the problem in a different way to allow faster convergence.
The intuition behind this approach is to combine MCMC (which efficiently
produces biased samples) with rejection sampling (which inefficiently produces
unbiased samples). On one set of nodes, we run many parallel copies of an
inefficient rejection sampler for a distribution s that only has a
probability ɛ of generating a sample. Whenever we generate a sample, we send
it asynchronously via MPI to a shared buffer.
On another set of nodes, we run many parallel copies of an efficient but biased
MCMC sampler that normally uses a symmetric proposal p(x2|x1) and accepts
proposals with probability min(1, p(x2|x1)s(x2)/p(x1|x2)s(x2)) = min(1, s(x2)/s(x1)). However, these MCMC samplers are modified to teleport with
probability ɛ to a random rejection sample they claim from the shared
buffer (which they always accept). We can see that this modified proposal still
satisfies detailed balance:
If a rejection sample is unavailable, we block until one is generated, but because the teleportation probability is related to the rate at which we can generate rejection samples (and because we have many nodes independently generating rejection samples), we are unlikely to be blocked by the unavailability of samples. This process ideally allows us to calculate unbiased expectations using MCMC even though our target distribution is multimodal.
To evaluate this method, we would determine if:
- sampling with teleportation gives more accurate expectations than sampling without, for various proposals and numbers of iterations
- splitting nodes between rejection sampling and MCMC performs better than simply allocating all nodes to one or the other
- there is an ideal ratio / teleportation probability
ɛfor a given distributionsthat determines how we should allocate our nodes
We have implemented this teleporting scheme in sequential code, but plan to parallelize it using MPI (for interchain communication and aggregation) and OpenMP (to parallelize rejection sampling locally on each node).
We have parallelized the normal MCMC algorithms with MPI on Odyssey (using pymc3 and mpi4py). Code is available here.
A natural model to test these methods on is a mixture of Gaussians. These distributions are naturally multimodal, but their full distribution is known and easy to sample from, so we can easily evaluate a number of exact rather than approximate convergence metrics. We can also vary the parameters of the mixture (i.e. the proximity and width of each mode as well as the number of modes and dimensions) and evaluate how our convergence metrics differ under these conditions.
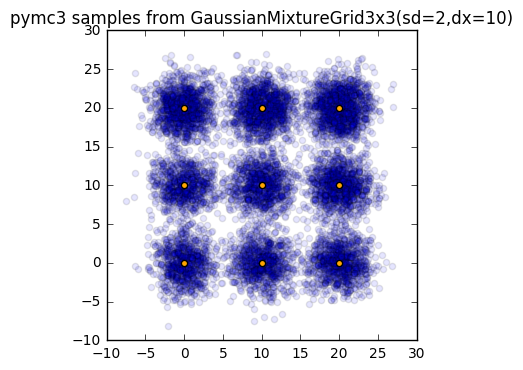
For the above mixture of 2D Gaussians, which overlap significantly, it is easy for MCMC methods to converge quickly:
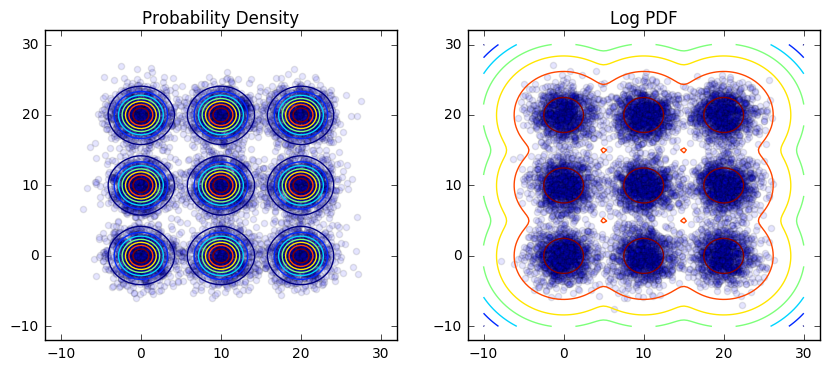
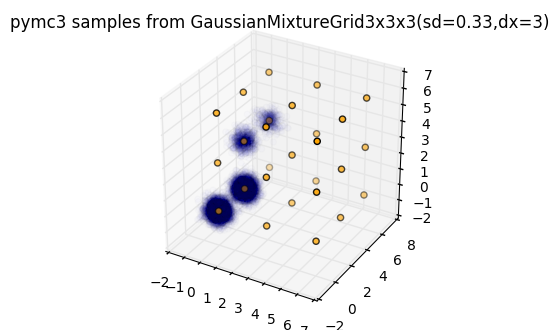
However, when we try to sample from a lattice of 3D Gaussians, convergence is more difficult to achieve:
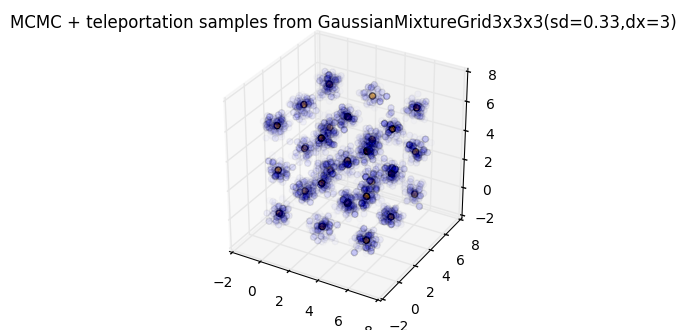
If we switch to our teleporting sampler (with ɛ≈0.05), our samples appear
much less biased:
We are working on larger scale convergence results for this scheme vs. MCMC vs. rejection sampling, as well as finding a suitable real-world dataset to test against.