RandLib

With RandLib one can easily work with probability distributions. One of the major advantages of this library (apart from being free and open-source) is that it doesn't require any additional packages. All you need is C++17 compiler support.

What can be done via RandLib? Here are some useful examples:

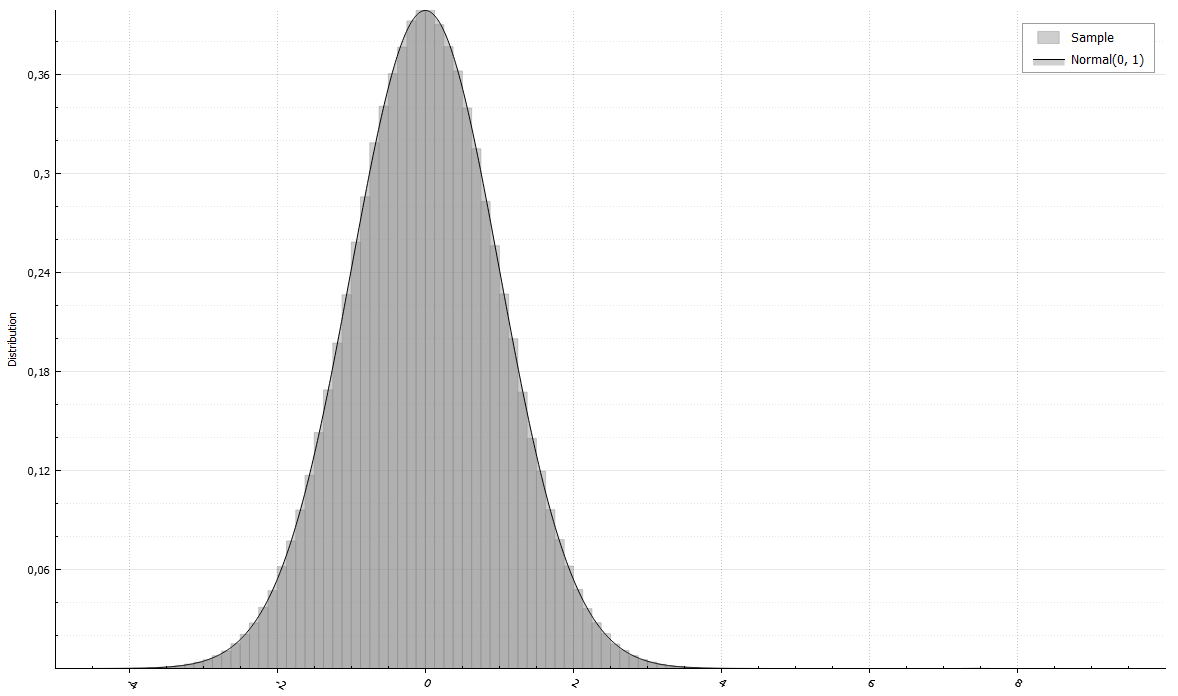
Fast sampling. For instance, generate million variates from standard normal distribution:

NormalRand X(0, 1);
std::vector<double> data(1e6);
X.Sample(data);

Calculate moments and other properties:

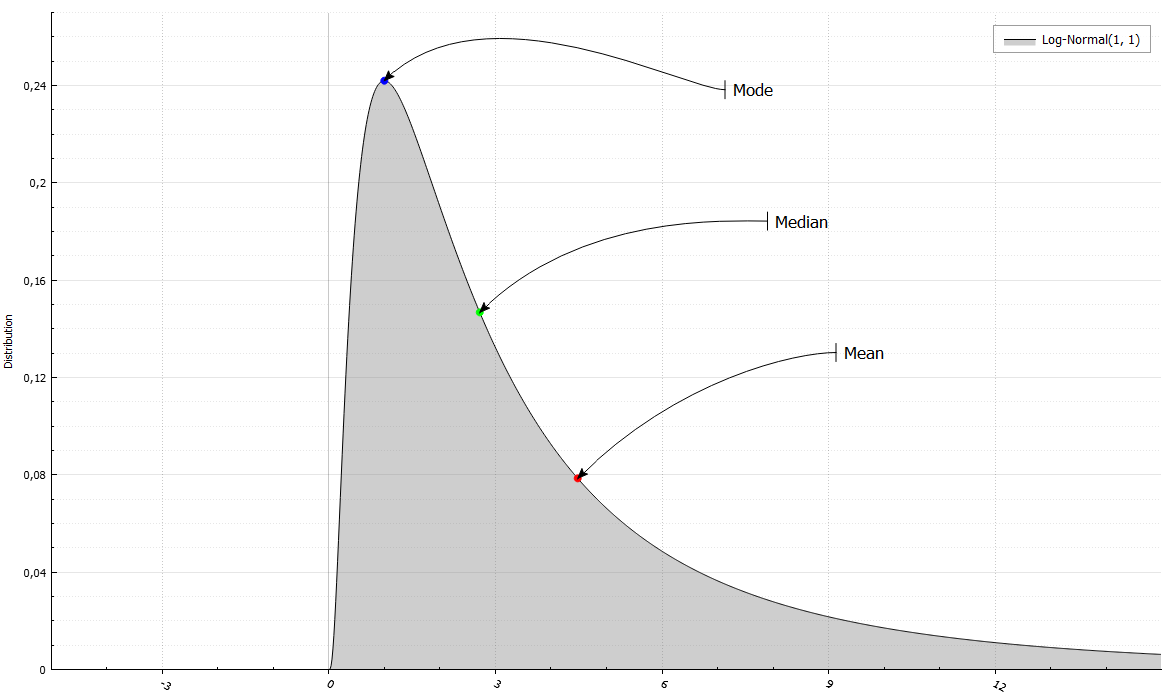
LogNormalRand X(1, 1);
std::cout << " Mean = " << X.Mean()
          << " and Variance = " << X.Variance()
          << "\n Median = " << X.Median()
          << " and Mode = " << X.Mode()
          << "\n Skewness = " << X.Skewness()
          << " and Excess kurtosis = " << X.ExcessKurtosis();

Mean = 4.48169 and Variance = 34.5126
Median = 2.71828 and Mode = 1
Skewness = 6.18488 and Excess Kurtosis = 110.936

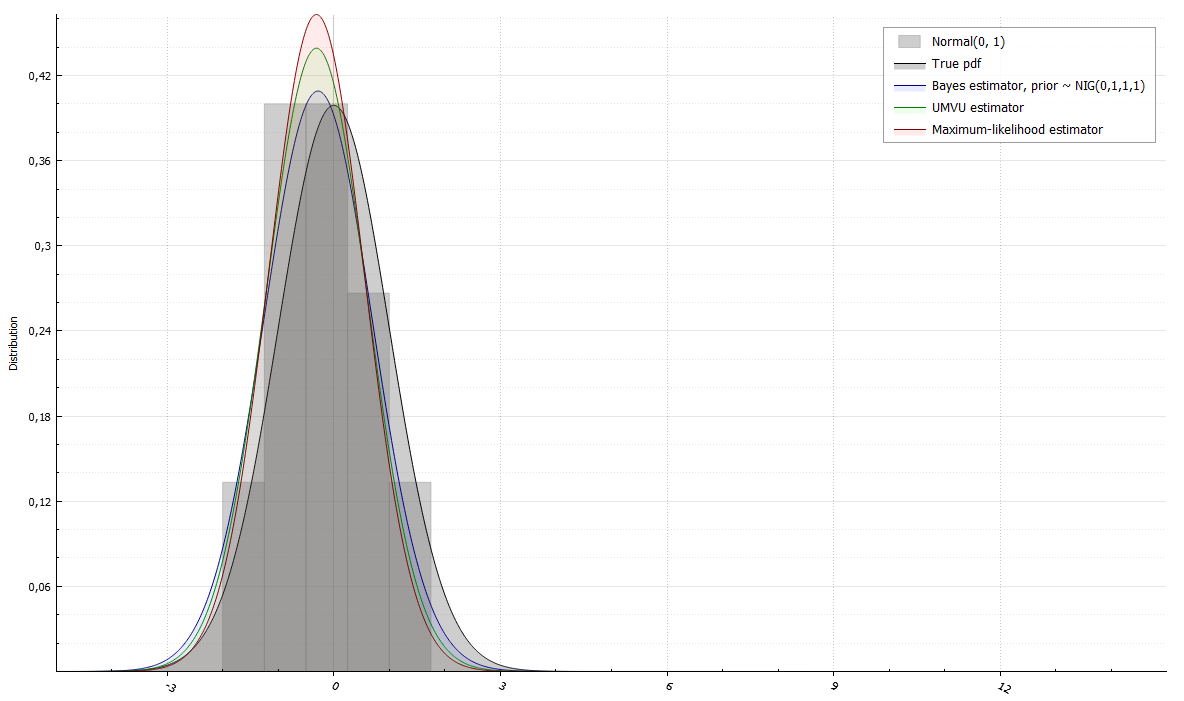
Fitting parameters using different estimators:

using std::cout;

NormalRand X(0, 1);
std::vector<double> data(10);
X.Sample(data);
cout << "True distribution: " << X.Name() << "\n";
cout << "Sample: ";
for (double var : data)
    cout << var << "  ";
cout << "\n";

/// Bayesian estimation
NormalInverseGammaRand prior(0, 1, 1, 1);
NormalInverseGammaRand posterior = X.FitBayes(data, prior);
cout << "Bayesian estimator: " << X.Name() << "\n";
cout << "(Posterior distribution: " << posterior.Name() << ")\n";

/// Uniformly minimum variance unbiased estimator
X.Fit(data, true);
cout << "UMVU estimator: " << X.Name() << "\n";

/// Maximum-likelihood estimator
X.Fit(data);
cout << "Maximum-likelihood estimator: " << X.Name() << "\n";

True distribution: Normal(0, 1)
Sample: -0.328154  0.709122  -0.607214  1.11472  -1.23726  -0.123584  0.59374  -1.20573  -0.397376  -1.63173
Bayesian estimator: Normal(-0.283042, 0.951348)
(Posterior distribution: Normal-Inverse-Gamma(-0.283042, 11, 6, 4.75674))
UMVU estimator: Normal(-0.311347, 0.82504)
Maximum-likelihood estimator: Normal(-0.311347, 0.742536)

For documentation look up here

astralord/RandLib

RandLib