averyanalex/quantpiler

Сompiler of classical algorithms into oracles for quantum computing

Сompiler of classical algorithms into oracles for quantum computing

Achievements:

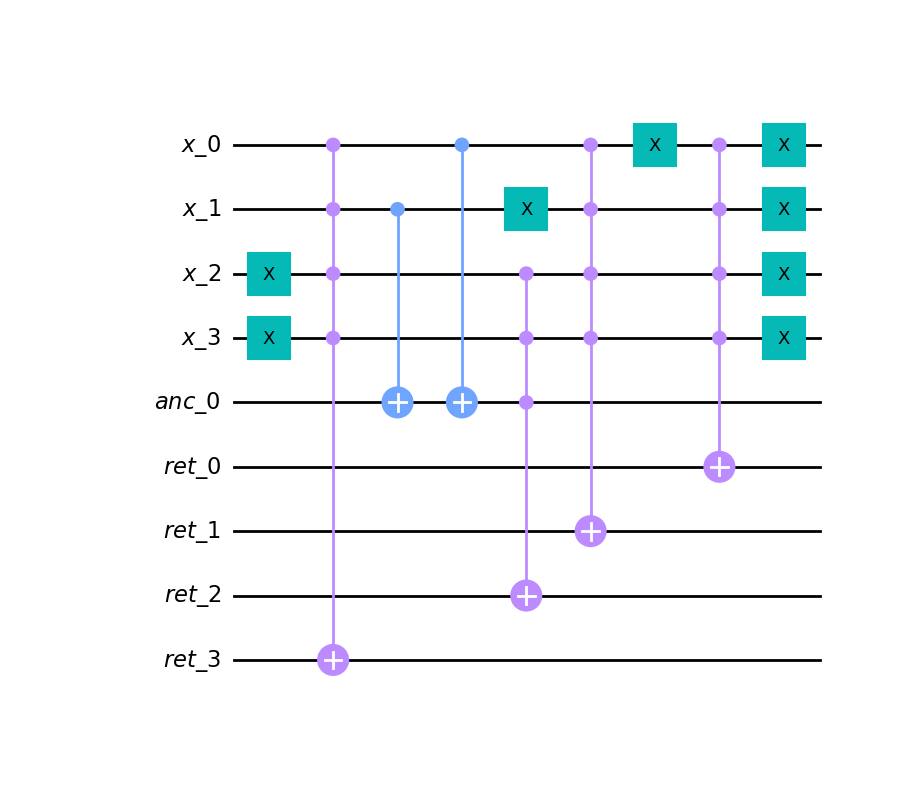
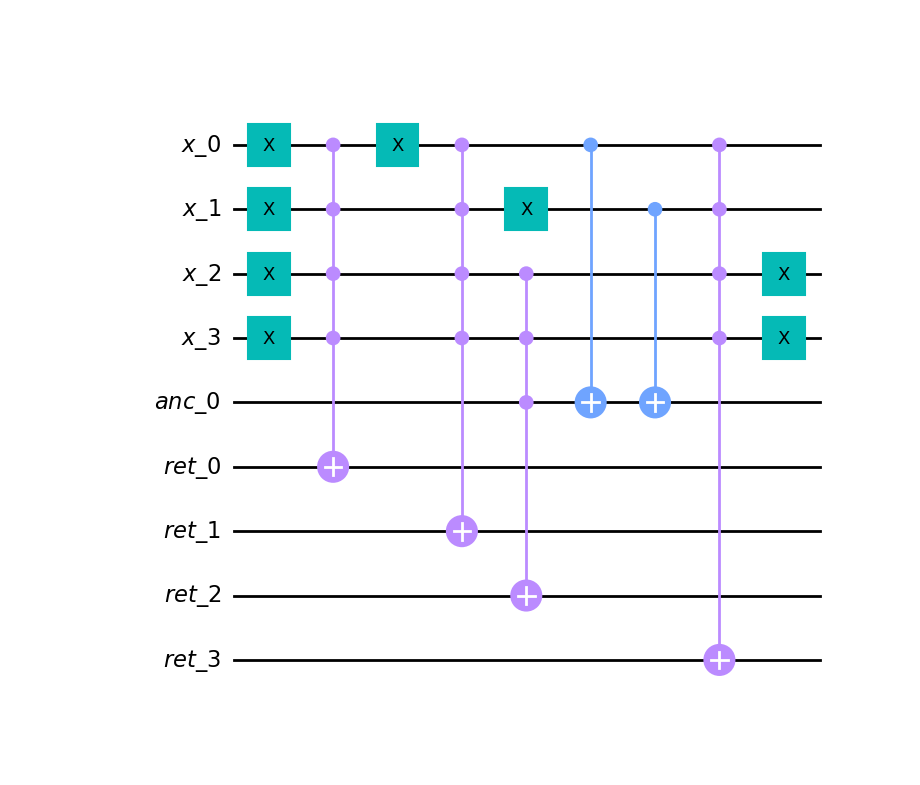
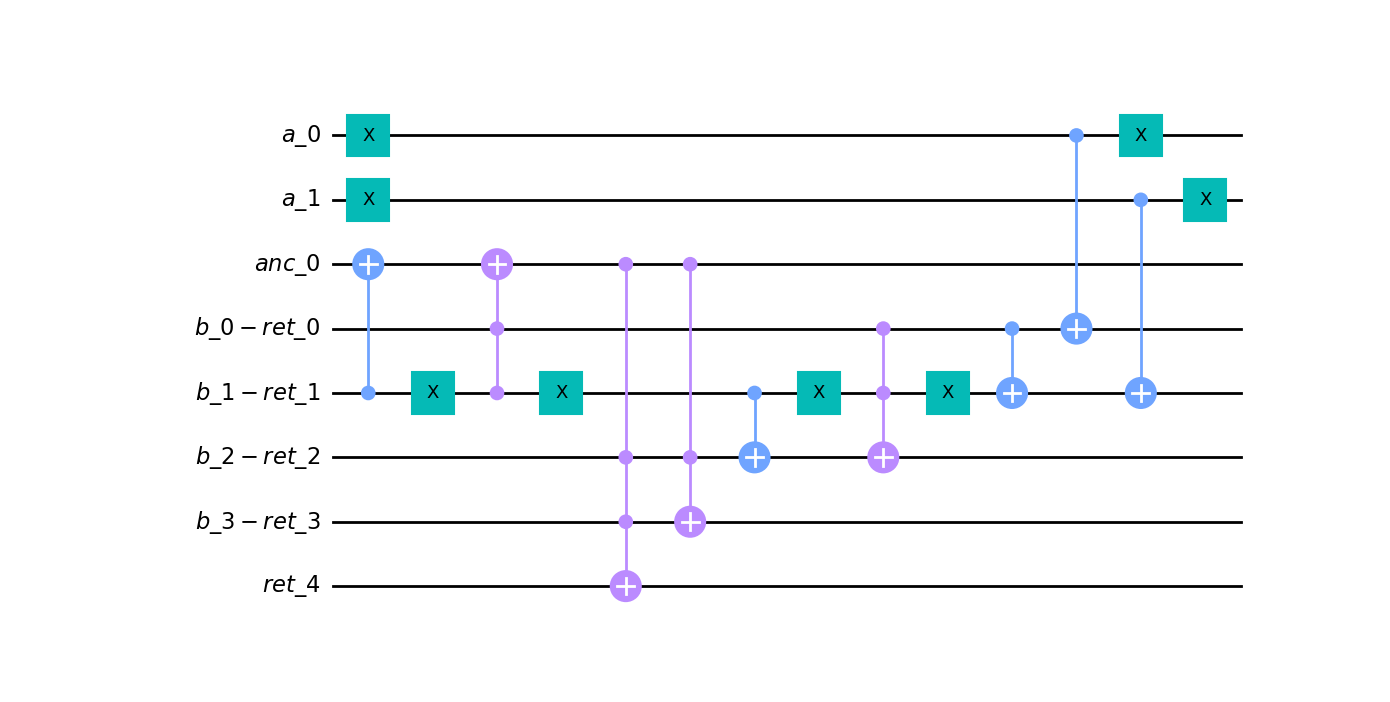
• CRC32 hash function (4 byte input) - 116 qubits.

Architecture:

1. Building expression.
2. Optimizing expression.
3. Constructing list of logical gates (logical expressions) for each bit of optimized expression.
4. Logical gates optimization (minimizing unique logic operations and qubit allocations).
5. Generation of a quantum circuit from a DAG of logical gates.

Authors:

• Alexander Averyanov - author
• Evgeny Kiktenko - mentor
• Dmitry Ershov - helped with the optimizer design

Example:

import quantpiler

x_len = 4
x = quantpiler.argument("x", x_len)

a = 6
# N = 2**4

prod = 1
for i in range(x_len):
    prod = ((x >> i) & 1).ternary(prod * a**(2**i), prod) & 0b1111

circ = prod.compile()
qc = quantpiler.circuit_to_qiskit(circ)

qc.draw("mpl")

# returning ancillas and arguments to their original state
rqc = quantpiler.circuit_to_qiskit(circ, rev=True)

rqc.draw("mpl")

User guide

Installation

pip install quantpiler

Binary releases on PyPI only available for Windows (x86, x86_64) and GNU/Linux (x86_64).

Now you can import library in Python:

import quantpiler

Creating input variables

a = quantpiler.argument("a", 2)
b = quantpiler.argument("b", 4)

This will create argument "a" with length of 2 qubits and "b" with length of 4 qubits. You can't use arguments with same name but with different lengths.

Expressions

Any argument variable, constant, or combination thereof is an expression. Expressions are actually lists of logic gates representing each bit. For example, a ^ b is effectively [[a[0] ^ b[0], [a[1] ^ b[1], b[2], b[3]].

Output expression lengths

Let's a -- length of first operand, b -- length (value for bitshifts) of second operand.

Name	Notation	Length
Binary invert	~	a
Bitwise XOR	^	max(a, b)
Bitwise OR	|	max(a, b)
Bitwise AND	&	min(a, b)
Sum	+	max(a, b) + 1
Product	*	a + b
Right bitshift	>>	a - b
Left bitshift	<<	a + b

Length is the maximum possible length of result. Actual length depends on optimizer decitions: for example, the length of a ^ a will be 0 (no qubits, empty expression).

Estimating length of expression:

# you can use builtin python's len to get estimated expression's length
length = len(a ^ b + 1)

Please note that this is an estimated length as actual length may vary depending optimizer solutions.

Debugging expression:

print(str(a ^ b + 1))

or, for jupyter:

a ^ b + 1

This will print (^ "a(2)" (+ 1 "4(2)")) for a of length 2 and b of length 4.

Bitwise binary operations

r = ~a
r = a ^ b
r = a | b
r = a & b

You can also do this with constants:

r = 0b101 ^ a
b |= 1
r = b & 0b11

Bit shifting

r = a << 2
r = b >> 3

Please note that only constant distance shifting is supported at this time.

Arithmetic operations

r = a + b
r = 2 * a * b

Ternary operations

If you want to emulate if statements, i.e.

if cond:
    r = a + b
else:
    r = b & 0b11

you can use ternary operators:

r = cond.ternary(a + b, b & 0b11)

Note that cond must be an expression exactly 1 qubit long. You can achieve this by using bitwise and with 1.

Compiling

Let's compile something:

r = a ^ b + 3

# internal circuit representation
circ = r.compile()

# QuantumCircuit from qiskit
qc = quantpiler.circuit_to_qiskit(circ)

# let's draw our circuit
qc.draw("mpl")