awestover/cupgame

The cup game is a cool problem in theoretical computer science.

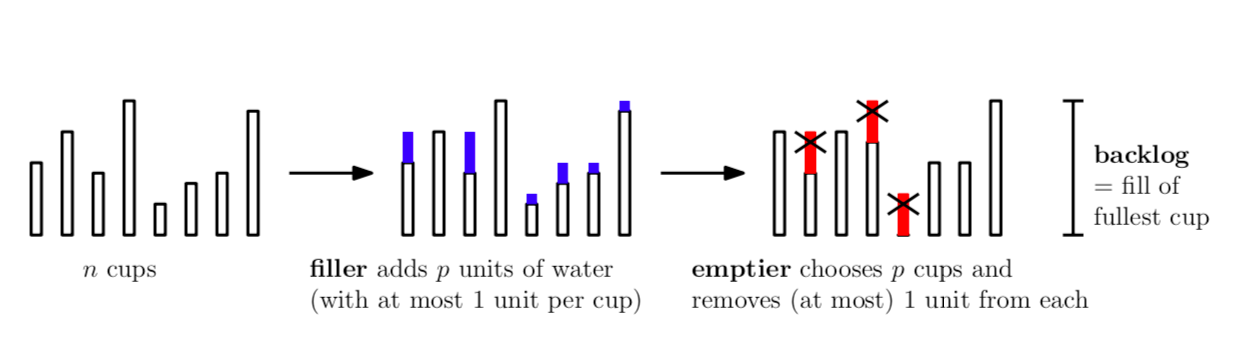
The Cup Game

The cup game is a classic problem in computer science that models work scheduling. In the cup game on n cups, a filler and an emptier take turns adding and removing water from cups (i.e. new tasks come in and the scheduler must allocate processors to handle the incoming work). On each round the filler will distribute some new amount of water among the cups, and the emptier will remove some amount of water from some of the cups. The filler can distribute the water however it wants (as long as it places at most a single unit of water in each cup), but the emptier has an added "discretization constraint": it can only remove water from some fixed number of cups (it removes a unit of water from each cup). The problem is to analyze how well each player can do, that is, how much water can the filler force to be in the fullest cup, and what is the upper bound on this fill that an appropriate emptying strategy can guarantee? We study several variants of the problem and answer some open questions.

results

• (main results) Variable-Processor cup game

We ask the natural question: "what if the number of processors is allowed to change?" Allowing the filler to change the resources drastically alters the game.

• An adaptive filler can achieve backlog linear in the number of cups! Classically there is a logarithmic upper bound! Wow!
  • An adaptive filler can achieve backlog $\Omega(n^{1-\epsilon})$ for constant $\epsilon$ in running time $2^{\log^2 n}$
  • An adaptive filler can achieve backlog $\Omega(n)$ in running time $O(n!)$
• A greedy emptier never lets backlog exceed $O(n)$
• An oblivious filler can still get polynomial backlog! But only against "greedy-like" emptiers.
  • In particular, we show that an oblivious filler can achieve backlog $\Omega(n^{1-\epsilon})$ against an $O(1)$-greedy-like emptier with probability at least $1-2^{-\polylog(n)}$ in running time $2^{\polylog(n)}$.

• (minor result) Multi-Processor Cup Game: Adaptive lower bound

We provide a simple construction that an adaptive filler can use to get large backlog. Combined with previous work by Kuszmaul this implies that backlog $\Theta(\log n)$ is tight for the adaptive case of the multi-processor cup game, regardless of the number of processors.