A camera projects 3D world-points onto the 2D image plane. Traditional cameras have some internal parameter which affect imaging process such as, Image center, Focal length and Lens distortion parameters. In addition to this almost unknown (actually all manufacturers gives their parameters but note that focal lenght will be change when you zoom in or out, and also in order to pyhsical deformations, other parameters might be changed as well) instrinsic parameters, if you want to calculate depth information of scene or 3d scene reconstruction, you have to know positions of cameras according to any reference point. In case of stereo vision application, one camera can be selected as reference point too. That time we need to know rotation and translation of one camera according to another in addition to instrinsic parameters. Generally 1 checkerboard plane is widely used for this aim. Accoding to theoretical background, we need at least 3 different view of one checker board image for all camera. But the more and different image you take, the better accuracy you gain. But if we use 2 or 3 ortogonal checkerboard, we can obtain both instrinsic and extrinsic parameters using only one shot.
In this research, we developed fully automatic 3 orthogonal checkerboards calibration techniques either mono or stereo camera. Actually we calculated the extrinsic parameters according to outher reference point which is intersection point of 3 orthogonal plane.
The main issue of this task is find all necessary point and their world plane positions automatically. To reach this aim, we make some assumtions, such the X,Y plane checkerboard should be 7x6 points, Y,Z plane checkerboard should be 8x6 points, and X,Z plane checkerboard should be 6x8 points. In this way we can easily recognize which sensed plane refers which plane. And also in order to prevent some confussion of intersection line of 3 planes, we do not use that the first row of intersection lines. The row image of our left camera image is in following figure.
We manually painted the intersection part of the plane to get the calibration size become as how we desing. Please note that does not mean we all need manual painiting. if you use appropriate calibration checkerboard, you wont need any pre-processing. After all we detect all planes, their image plane locations in superpixel resolution and their real word locations as you can see in following figure. You can find the code that perform this result in following function;
> [Ipoints Wpoints]=findpoints768686(Iin,sg,pk)
where Iin is the RGB image, sg is sigma value we used it sg=2, and pk is peakThreshold value we selected it 0.15 in our test. It return world plane point location and image plane point locations. Please note that function was written hard coded manner. But you can easily change it according to your demands. Please note in following figure, you see just unit coordinate. We multiply that unit coordinate to 2.8 where each small square length is 2.8 cm. So our final translation results will be in cm.
Assume we say ith point’s real world coordinate is [xi,yi,zi] and its camera image plane pixel locations is [pxi,pyi]. According to Hall algorithm the camera model should be represented by 3x4 matrix A, whose bottom left element is 1. So, we can define calibration matrix as followings.
A=[a1 a2 a3 a4;a5 a6 a7 a8;a9 a10 a11 1] To calculate 11 unknown element of A, First of all, we should define matrix Q and matrix B as follows.
Q=[x1 y1 z1 1 0 0 0 0 -px1x1 -px1y1 -px1z1; 0 0 0 0 x1 y1 z1 1 -py1x1 -py1y1 -py1z1;........;xn yn zn 1 0 0 0 0 -pxnxn -pxnyn -pxnzn; 0 0 0 0 xn yn zn 1 -pynxn -pynyn -pynzn]
As above equation Q matrix have to has 2n rows and 11 columns. Subsequent two rows is belongs to the certain order fo data points. For instance first 2 rows are for 1st element, 3 and 4 th rows are for 2nd element and so on so forth. In that equation n is the number of points which we know the correspondence of those points both 3d location and their image plane locations. B=[px1;py1;.....pxn;pyn]
As you can see above, B matrix has just one column matrix (actually it is a vector) it has 2n number of rows where subsequent two rows are belong to certain points image location as x and y. First two rows is x and y location of 1st pixel, 3 and 4 rows are x and y location of second pixel so on so forth. To solve the unknown camera matrix A we should solve following equation
Q*[a1;a2;.....a11]=B
To solve above equation, we can use least square error minimization which can be known as pseudo inverse process. As a result we can calculate unknown “a” vector with followings.
[a1;a2;.....a11]=(Q^T Q)^(-1) Q^T B
After finding unknown 11 element “a” vector, we can reconstruct A matrix which was describe above. Using found A matrix we can calculate the points image plane pixel location when we know its 3d location using following equations.
[kxi;kyi;ti]=A.[xi;yi;zi;1]
Where, predicted pixel locations pxi and pyi can be calculated with followings
pxi=kxi/ti, pyi=kyi/ti
After that, we can calculate the distance of given image plane locations and predicted one with following equations.
di=sqrt(pxi-xi)^2+(pyi-yi)^2)
Normally we expect the distance could be as low as possible.
Above explanation is not for if corresponded points location has significant error. If there is significant error then we can use RANSAC algorithm to get rid of noisy data. To do than we do not take all given data points and its correspondences. Because some of them could be outlier and it could be cause of wrong prediction of camera parameter. According to RANSAC algorithm we just select minimum number of random data points in given correspondences [xi,yi,zi,pxi, pyi]. Since Q matrix has 11 element ( in other words we have 11 unknown params in A matrix) we need at least 11 equations. For every data point we obtain 2 equations ( 2 rows) so if we have 6 data points we obtain 12 equations (12 rows of Q matrix) then we can obtain A matrix. It means in every iteration we should select random 6 different data points and its correspondence. Within those [x1,y1,z1,px1, py1,....,x6,y6,z6,px6, py6] we can calculate Q and B matrix then we can calculate A matrix. Using this found A matrix e can predict all given 3d points image plane location prediction and we can calculate how many data points distance is less than certain threshold. We should do this process in certain number of times. ( for instance 10000 times, select random 6 data calculate Q B and then find A matrix then predict location and calculate distance) our aim is find 6 random points where the model which created with this 6 data point has maximum number of inlier data. To do that we always count how many data points has less distance then any certain threshold. When the maximum number of iteration is finished, then we should use the A matrix which is the best model we can find.
With above explanation we obtain camera model A, but we should decompose camera intrinsic and extrinsic parameters.
u0=(a1a9+a2a10+a3a11)/(a9^2+a10^2+a11^2)
v0=(a5a9+a6a10+a7a11)/(a9^2+a10^2+a11^2)
where ⊗ is cross product operator and ‖ ‖ is norm operator
αu=‖[a1 a2 a3 ]⊗[a9 a10 a11 ]‖/(a9^2+a10^2+a11^2)
αv=‖[a9 a10 a11 ]⊗[a5 a6 a7 ]‖/(a9^2+a10^2+a11^2)
Intrinsic camera parameter K as follows;
K=[αu 0 u0; 0 αv v0; 0 0 1]
Lets assume that Extrinsic R matrix is 3x3 martix and T Extrinsic matrix is 3x1 matrix as depicted follows.
R=[r1 r2 r3;r4 r5 r6;r7 r8 r9],T=[tx;ty;tz]
We can calculate tz as follows
tz=1/(a9^2+a10^2+a11^2)
Then R T K and found A matrix should meet following equation
K[R T]=A.tz
K A and tz are known. So we can take inverse of K matrix and multiply it with right side of equation to find the R and T matrix. [R T]=K^(-1)Atz
Then we can figure out what is the element of R and T easily.
According to our test we took following R , T, and K values for left camera;
R1 =
-0.6882 0.7250 0.0292
0.5059 0.5001 -0.7028
-0.5241 -0.4689 -0.7109
T1 =
1.6614
-4.7742
81.1783
K1 =
1649.4 0 793.3
0 1654.1 614.4
0 0 1
For right camera, we took following output.
R2 =
-0.9322 0.3617 -0.0112
0.2732 0.6621 -0.6979
-0.2450 -0.6536 -0.7161
T2 =
6.6994
-2.3526
77.8675
K2 =
1631.7 0 789.1
0 1625.7 634.8
0 0 1
To interpret the result we found focal length fx=1631.7, focal lenght fy=1625.7, center of image is (789.1 634.8) for right camera. please note our images has 1200x1600 resolution which means expected center point is (800,600). For extrinsic parameter, we found rotational matrix but it is not understandable for us. To get it more nderstandable, we need to convert it into vector with following comamnd.
rot = rotationMatrixToVector(R1)
-0.5262 -2.7480 1.1218
now you can see all rotations for both x, y and z axis respectively for right camera. but what about translation?. So what we know about the position of both left and right camera according to intersection point reference?. Since referencePoint(0,0,0)= R*Camera+T, So Camera=-R'*T. To do that we need to run following commmand.
> -R1'*T2
> -R2'*T2
left camera position
46.0793
39.2640
54.3177
right camera position
25.9359
50.0053
54.2249
You can see relative transformation from Left camera to the right camera with following commands.
R=R2*R1'
T=T2-R*T1
R =
0.9038 -0.2757 0.3275
0.2804 0.9593 0.0336
-0.3234 0.0615 0.9443
T =
-22.92279
-1.74840
3.81712
Also in that expression please note that TT variable means translation from left to right and its norm is the same almost 23 which menas the cameras have 23 cm baseline again.
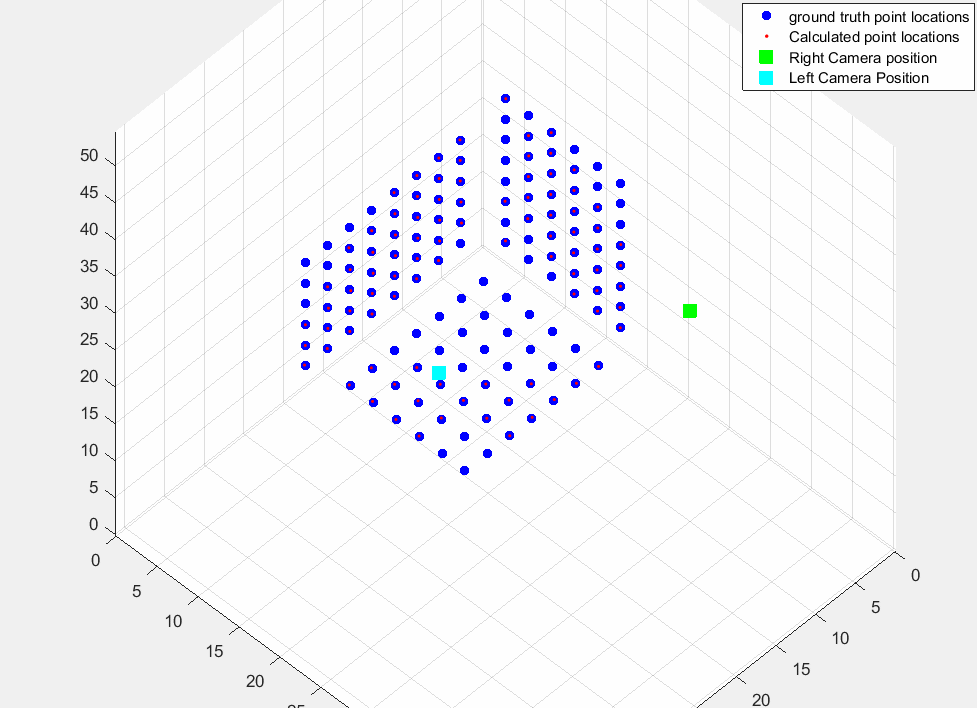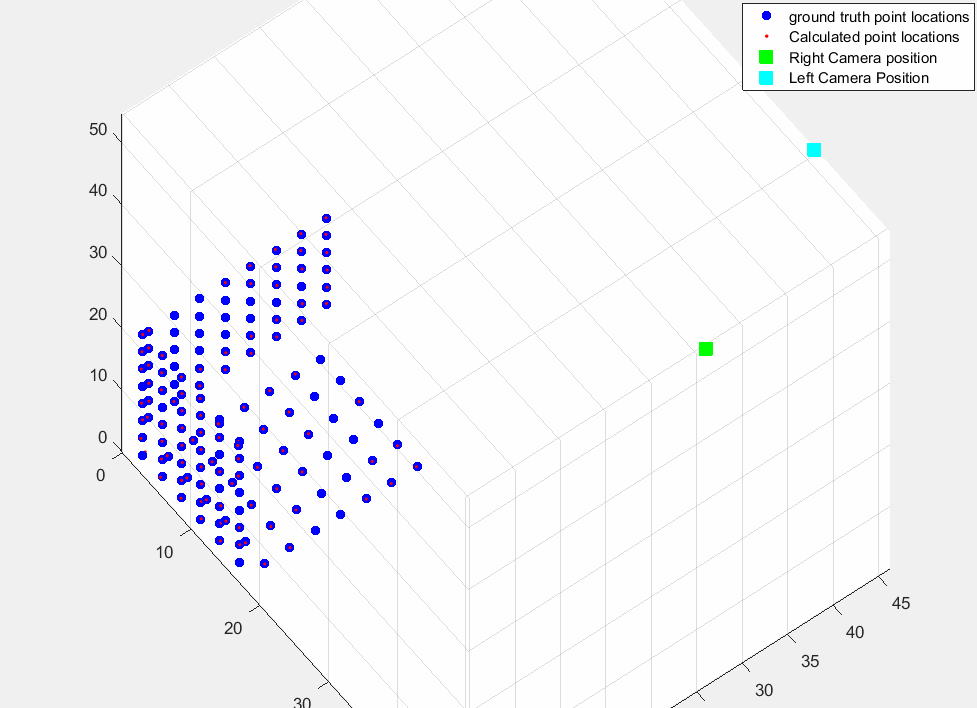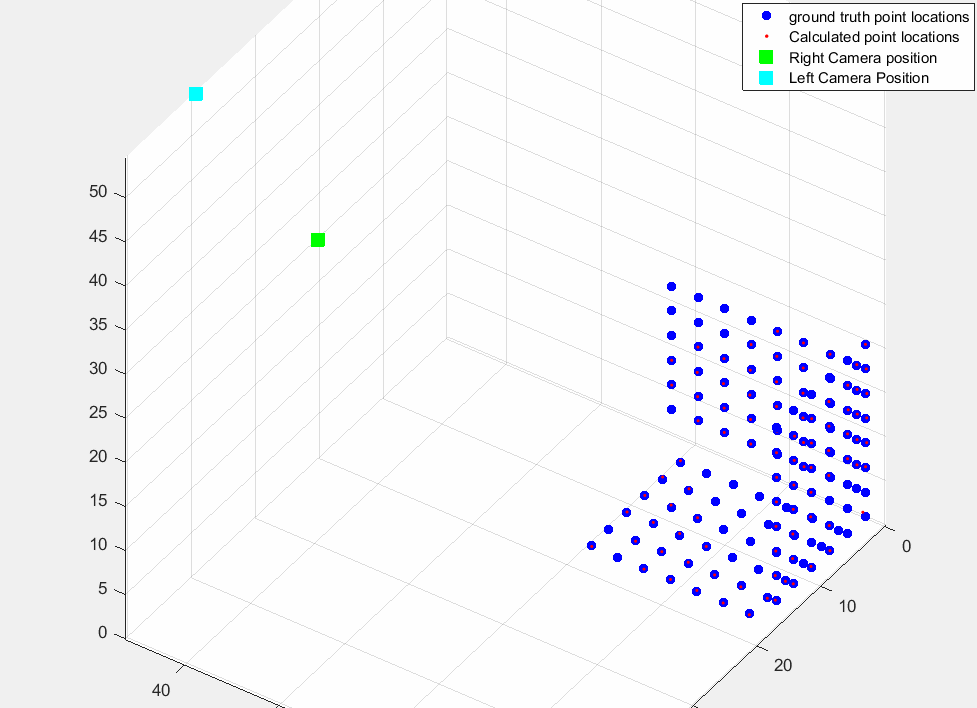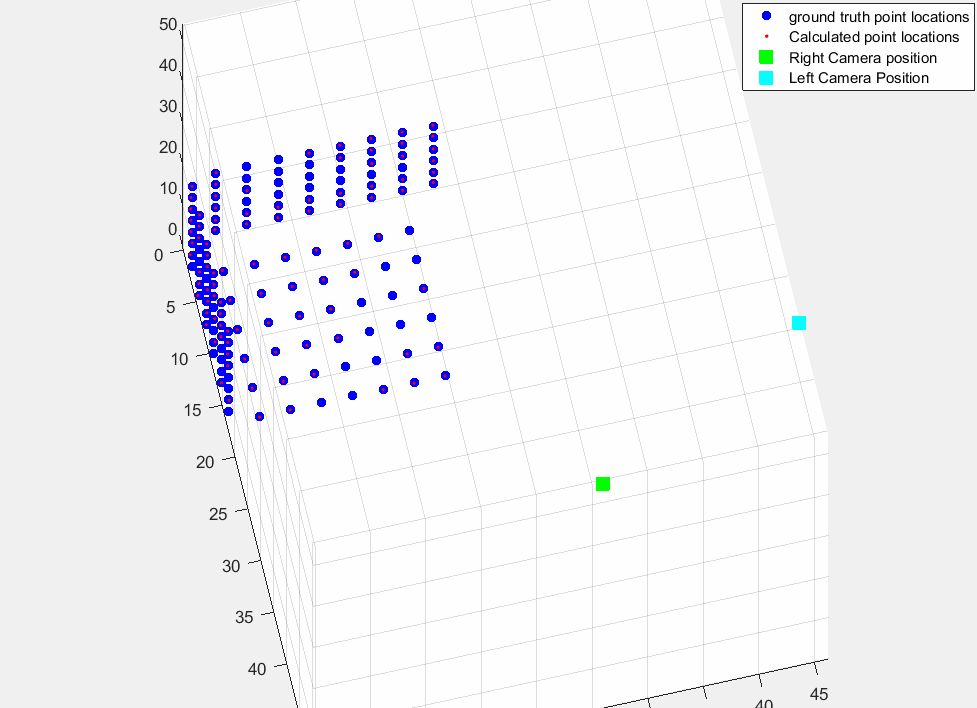
Here you saw x,y,z position of both cameras. the norm of left camera is around 81.3 which means it has 81.3cm distance to the reference point (plane intersection point). And if you calculate norm of relative position of cameras you will see there is almost 23 cm differneces between these two cameras which is baseline of our stereo vision system.
At the end, we can plot groundt truth point positions, calculated positions from stereo camera using triangulation, and both two camera positions as following figure.
Fundamental and Essential matrixes are so important to find epipolar line. Here is how we calculated these matrix and their results.
> tx = [0 -T(3) T(2); T(3) 0 -T(1); -T(2) T(1) 0];
> E = tx * R
> F = K2' \ E / K1
E =
-0.1029 -20.2744 -16.3279
-59.5467 8.1424 224.3821
-50.0707 -226.5122 -3.5875
F =
-0.0000 -0.0000 -0.0053
-0.0000 0.0000 0.1528
-0.0159 -0.1317 10.1045
To show how we can find epipolar line on right image for pixel of (218,398) position in left image here is the given command and found epipolar line
> lf=F*[218;398;1];
> spx=[1 size(IinR,2)];
> spy(1,1)=(-lf(3)-lf(1)*spx(1))/lf(2);
> spy(1,2)=(-lf(3)-lf(1)*spx(2))/lf(2);
> figure;imagesc(IinR);hold on;
> plot(spx,spy,'b-','linewidth',4);
We know all rotations and translation. also we know the query point on the left is on y=0 plane. Within th eepipolar line we know that query points on that line, but can we calculate its exact position?. Within the knowledge of that point is on y=0 plane, we can do it. Suppose H=K1x[R1 T1] and H is 3x4 matrix. we assume all elemen of H is h11 , h12 ..to h34. So if query point location is [X;0;Z] we can write following equation.
λ[218;398;1]=Hx[X;0;Z;1]
Since 2nd elemen of world coord vector is 0 and last one is 1 as known parameter we rewrite the equation as follows;
λ[218;398;1] -[h14;h14;h34]=[h11 h13;h21 h23;h31 h33]x[X;Z]
since we do not know λ, there are X,Y, λ unknow variable and we collect them on the left and rewrite them as a matrix form as follows.
- -[h14;h14;h34]=[h11 h13 -218;h21 h23 -398;h31 h33 -1]x[X;Z;λ]*
now we can calculate unknow part with matrix inversion as follows.
- [X;Z;λ] = - inv([h11 h13 -218;h21 h23 -398;h31 h33 -1])x[h14;h24;h34]*
So within that calculation, we found X and Z, as we know Y=0, so it is quite easy to calculate any X,Y,Z world coordinate point to the right image coordinate as follows;
- [λpx;λpy;λ]=K2*[R2 T2]*[X;0;Y;1] *
note we should divide λpx and λpy to λ to find exact pixel position. here is how we calculate it in matlab and find point on image.
H=K1*[R1 T1];
w=inv([H(:,1) H(:,3) -[218;398;1]])*-H(:,4);
W(1,1)=w(1);
W(2,1)=0;
W(3,1)=w(2);
q=K2*[R2 T2]*[W;1]
ip=q/q(3);
plot(ip(1),ip(2),'r*','MarkerSize',10);
Here is the query point of the left camera image, its epipolar line on the right camera image and assumption of this point on Y=0 plane, its exact position on right image. as you can see the epipolar line is not parallel,that is because the cameras were not mounted at the same straigth line properly.
You can run all steps with just one main script as following command.
> main