/tmc-analysis

Voltage and current distribution analysis of a resonant lumped LC circuit

Primary LanguageMATLABMIT LicenseMIT


Logo

Tune & Match Circuit Analysis

About the project

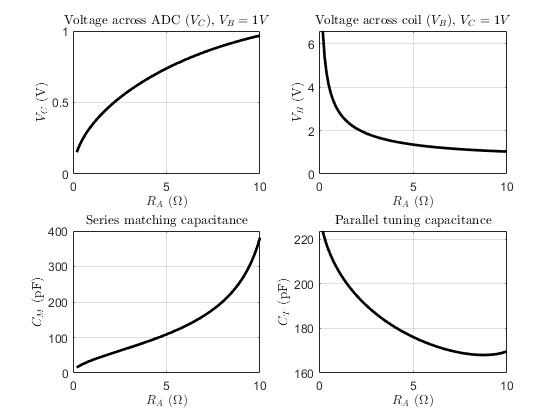
The script computes the the transformation of 1V incduced by a:

  • locally tuned and matched reciever across a 50 ohm receiver terminal.
  • A 50 ohm reciever (geneartor) across the terminals of a locally tuned and matched coil.

Software

  • MATLAB

circuit

Computation

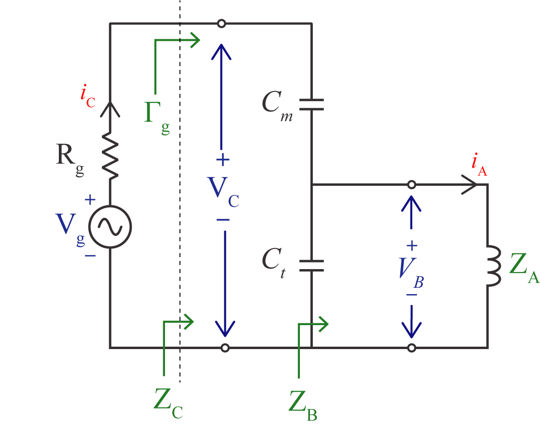
Complex coil impedance is defined as:

Z_A = R_A+jX_A

The tuning (Ct) and matching (Cm) element values are found by solving the matching conditions

B = \frac{X_A\pm\sqrt{R_A/Z0}: \sqrt{R_A(R_A-Z_0)+X_A^2}}{R_A^2+X_A^2}

C_t = B/\omega_0

Z_B = \frac{1}{j\omega C_t+1/Z_A}

X = \frac{1}{B}+\frac{X_A Z_0}{R_A}-\frac{Z0}{R_A B}

C_m = \frac{-1}{\omega X}

Ct and Cm values are only valid when B and X are positive, therefore an appropriate sign is to be chosen in for the Ct equation. Subsequently, the input impedance of the parallel LC resonant circuit is defined as:

Z_C=Z_B+\frac{-j}{\omega C_m}

Voltage and current distribution (Generator POV)

The reflection coefficient looking through the generator terminals (Gen->Load)

\Gamma_G=\frac{Z_C-Z_0}{Z_C+Z_0}

The accepted power by the circuit from the generator is computed as

P_{in}=P_{av}(1-|\Gamma_G|^2)

As such the voltage induced across the generator terminals and current flowing through them are

V_C = \sqrt{4 P_{in} Z_C}

i_C = V_C /Z_C

Similallry the voltage induced across the parallel resonator is

V_B=V_C \cdot \frac{Z_B}{Z_B+jX}

The current flowing through the coil is evaluated by

i_A = V_B/Z_A

Therefore the power delivered to the coil is

P_L = \frac{1}{2}\mathbb{R} (i_A^*V_B)

(back to top)

Results


result

License

Distributed under the MIT License. See LICENSE.txt for more information.

Contact

Mohammed M. Albannay - @Bannay - bannay@gmail.com

Project Link: https://github.com/bannay/tmc-analysis

Acknowledgments

(back to top)