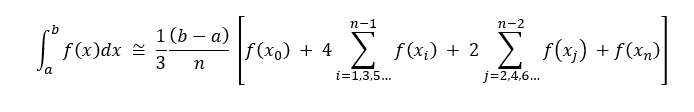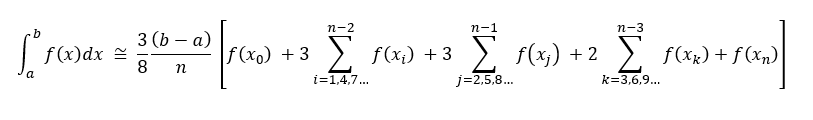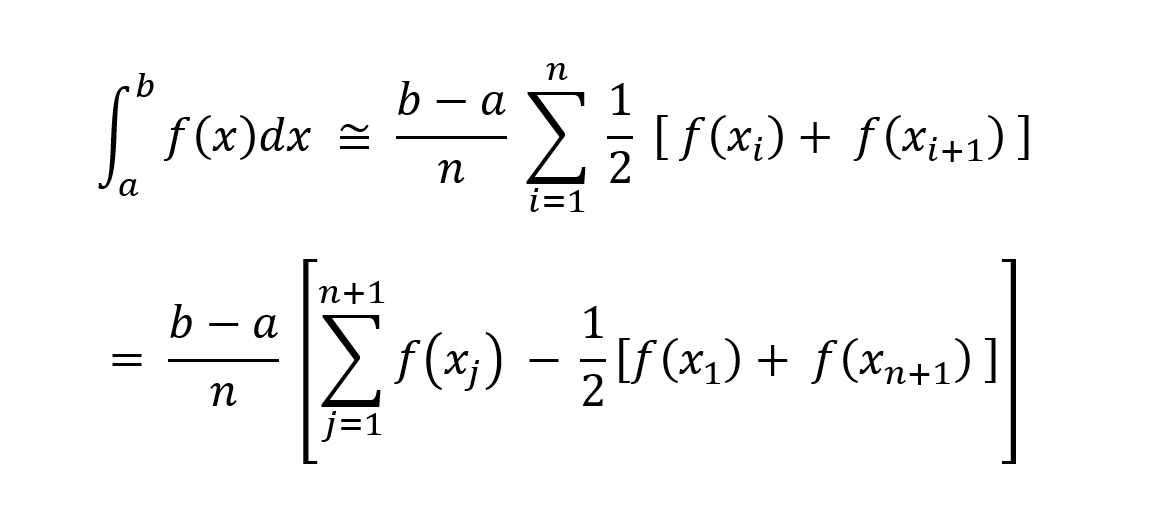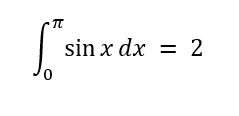Numerical Integration

Performs numerical integration on x-y data. Uses Simpson's Rule where applicable, and the Trapezoidal Rule in all other cases.

Returns the result, as well as a string indicating the method used.

    [method, result] = NumIntgrl(x, y);

Methods

Simpson's 1/3 Rule:

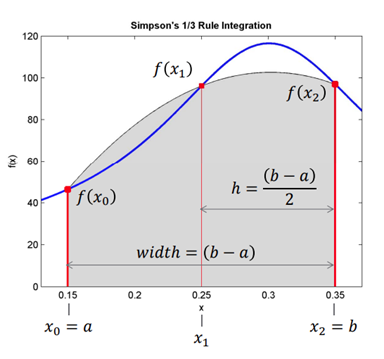
Approximates a function using 2nd order polynomials.

For n equal segments (i.e., n+1 evenly spaced data points), the definite integral can be approximated as follows. Note that n must be even.

Here (b-a)/n is the spacing between data points.

Simpson's 3/8 Rule:

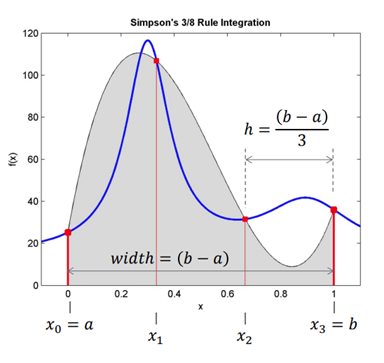
Approximates a function using 3rd order polynomials.

For n equal segments (i.e., n+1 evenly spaced data points), the definite integral can be approximated as follows. Note that n must be an integer multiple of 3.

Here (b-a)/n is the spacing between data points.

Trapezoidal Rule:

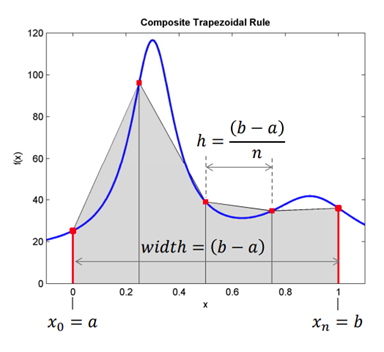
Approximates a function using trapezoids.

For n equal segments (i.e., n+1 evenly spaced data points), the definite integral can be approximated as follows.

Here (b-a)/n is the spacing between data points.

Test code:

for Npts = logspace(1, 4, 4) + 1
    x = pi*linspace(0, 1, Npts);
    y = sin(x);
    [method, result] = NumIntgrl(x, y);
    fprintf('n = %-6d \tTrapz = %.6f \t%s = %.6f\n', Npts-1, trapz(x, y), method, result)
end

n = 10     	Trapz = 1.983524 	Simp 1/3 = 2.000110
n = 100    	Trapz = 1.999836 	Simp 1/3 = 2.000000
n = 1000   	Trapz = 1.999998 	Simp 1/3 = 2.000000
n = 10000  	Trapz = 2.000000 	Simp 1/3 = 2.000000

for Npts = logspace(1, 4, 4)
    x = pi*linspace(0, 1, Npts);
    y = sin(x);
    [method, result] = NumIntgrl(x, y);
    fprintf('n = %-6d \tTrapz = %.6f \t%s = %.6f\n', Npts-1, trapz(x, y), method, result)
end

n = 9      	Trapz = 1.979651 	Simp 3/8 = 2.000382
n = 99     	Trapz = 1.999832 	Simp 3/8 = 2.000000
n = 999    	Trapz = 1.999998 	Simp 3/8 = 2.000000
n = 9999   	Trapz = 2.000000 	Simp 3/8 = 2.000000

for Npts = logspace(1, 4, 4) + 2
    x = pi*linspace(0, 1, Npts);
    y = sin(x);
    [method, result] = NumIntgrl(x, y);
    fprintf('n = %-6d \tTrapz = %.6f \t%s = %.6f\n', Npts-1, trapz(x, y), method, result)
end

n = 11     	Trapz = 1.986387 	Trap     = 1.986387
n = 101    	Trapz = 1.999839 	Trap     = 1.999839
n = 1001   	Trapz = 1.999998 	Trap     = 1.999998
n = 10001  	Trapz = 2.000000 	Trap     = 2.000000

Resources:

https://web.engr.oregonstate.edu/~webbky/MAE4020_5020_files/Section%208%20Integration.pdf

bdubs-astro/NumIntgrl

Numerical Integration

Methods

Simpson's 1/3 Rule:

Simpson's 3/8 Rule:

Trapezoidal Rule:

Test code:

Resources: