comvlong

The goal of comvlong is to facilitate the computation of a weighted disparity metric for police officers, which could be used in criminal proceedings under the guidance provided by the Massachusetts Supreme Judicial Court in Commonwealth v. Long. Please see VanDerwerken, Fowler, and Kadane (2023) for more information.

Installation

You can install the development version of comvlong from GitHub with:

# install.packages("remotes")
remotes::install_github("beanumber/comvlong")

Boston Police Department citations

library(tidyverse)
library(comvlong)

In March 2021, attorney Joshua Raisler Cohn of the Roxbury Defenders Unit made a public records request to the Boston Police Department for 10 years’ worth of citation data. These data were included in The Woke Windows Project and in nstory’s GitHub repository.

The comvlong package contains:

download_bpd_offenses(): a function to download the full 10-year dataset
bpd_offenses_20: a complete set of offenses for only the year 2020
bpd_stops_1120: a cleaned set of 10 years worth of stops (aggregated from the offenses)
several ancillary tables

The following table displays summary statistics for the citation data in the bpd_offenses_20 data frame.

bpd_offenses_20 |>
  group_by(issuing_agency) |>
  summarize(
    num_citations = n(),
    begin_date = min(event_date),
    end_date = max(event_date),
    num_officers = n_distinct(officer_id),
    num_offenses = n_distinct(offense)
  ) |>
  knitr::kable()

issuing_agency	num_citations	begin_date	end_date	num_officers	num_offenses
Boston Police Area A	52	2020-01-02	2020-11-01	1	22
Boston Police Area B	231	2020-01-01	2020-12-24	1	34
Boston Police Area C	152	2020-01-01	2020-12-28	1	27
Boston Police Area D	58	2020-01-01	2020-11-27	1	22
Boston Police Area E	1	2020-03-09	2020-03-09	1	1
Boston Police Area F	38	2020-01-03	2020-12-07	1	15
Boston Police Area G	3	2020-07-02	2020-08-16	1	3
Boston Police Area H	69	2020-01-01	2020-12-18	1	20
Boston Police Area J	31	2020-01-04	2020-10-19	1	16
Boston Police Area K	25	2020-01-01	2020-10-10	1	15
Boston Police Area L	8	2020-08-07	2020-09-09	1	4
Boston Police District A-1	1267	2020-01-01	2020-12-30	280	80
Boston Police District A-7	1942	2020-01-01	2020-12-10	198	75
Boston Police District B-2	5625	2020-01-01	2020-12-31	572	103
Boston Police District B-3	4237	2020-01-01	2020-12-31	452	110
Boston Police District C-11	4651	2020-01-01	2020-12-31	407	91
Boston Police District C-6	4446	2020-01-01	2020-12-31	433	85
Boston Police District D-14	1128	2020-01-03	2020-12-30	190	55
Boston Police District D-4	3848	2020-01-01	2020-12-31	554	100
Boston Police District E-13	2293	2020-01-01	2020-12-31	236	76
Boston Police District E-18	5362	2020-01-01	2020-12-31	395	99
Boston Police District E-5	5727	2020-01-01	2020-12-31	395	77
Boston Police Special OPS	1799	2020-01-01	2020-12-27	256	92

The table below shows the first few rows of the bpd_stops_1120 table.

bpd_stops_1120
#> # A tibble: 240,092 × 6
#> # Groups:   citation_number, officer_id, event_date, location_name [240,092]
#>    citation_number officer_id event_date          location_name race  
#>    <chr>           <chr>      <dttm>              <chr>         <chr> 
#>  1 019891AA        99877      2018-02-10 00:00:00 Dorchester    BLACK 
#>  2 019892AA        99877      2018-02-10 00:00:00 Dorchester    BLACK 
#>  3 019893AA        99877      2018-02-10 00:00:00 Dorchester    BLACK 
#>  4 019895AA        99877      2018-02-10 00:00:00 Dorchester    HISP  
#>  5 019896AA        99877      2018-02-10 00:00:00 Dorchester    BLACK 
#>  6 019899AA        99877      2018-02-10 00:00:00 Dorchester    BLACK 
#>  7 019901AA        99877      2018-02-10 00:00:00 Dorchester    HISP  
#>  8 020114AA        4159       2018-02-11 00:00:00 Roxbury       BLACK 
#>  9 020270AA        131215     2018-02-10 00:00:00 Boston        UNKNWN
#> 10 020630AA        99877      2018-02-12 00:00:00 Dorchester    WHITE 
#> # ℹ 240,082 more rows
#> # ℹ 1 more variable: num_offenses <int>

While the Boston Police Department can be used for many purposes, our goal is to use these to illustrate how the weighted disparity measure can be used in court proceedings to support a claim of racial bias against an individual police officer.

Weighted disparity

Let $n_{ij}$ be the number of stops made by officer $i \in I$ in location $j$, over some duration of time, and let $p_{ij}(r)$ be the proportion of those $n_{ij}$ stops in which the person who was stopped was identified as having race $r$. The goal of the weighted disparity measure is to contextualize the proportion $p_{ij}(r)$ in relation to officer $i$’s peers. More specifically, if it were officer $i$’s peers (in the set $I$) who had made those $n_{ij}$ stops in the same locations during the same periods of time, what proportion of those stops would likely be of people whose race is identified as $r$?

Since officer $i$’s patrol locations vary, as do the demographics of each location $j$, we define $w_{ij}$ to be a weight – the proportion of stops made by officer $i$ in each location $j$: $$ w_{ij} = \frac{n_{ij}}{\sum_{j \in J} n_{ij}}, $$ where $J$ is the set of all locations. Note that $\sum_{j \in J} w_{ij} = 1$.

Then for all officers other than officer $i$ patrolling location $j$, they stop people of race $r$ as: $$ p_{ij}^(r) = \sum_{k \neq i, k \in I} \frac{n_{kj}(r)}{n_{kj}} ,, $$ The difference $d_{ij}(r) = p_{ij}(r) - p_{ij}^(r)$ is the disparity between the behavior of officer $i$ relative to the other officers who patrol location $j$, with respect to race $r$. If $d_{ij}(r) > 0$, then officer $i$ has stopped people of race $r$ in location $j$ more often than his peers.

The weighted disparity measure $x_{ij}(r)$ is the weighted average of officer $i$’s disparity measures across all locations:

$$ x_{ij}(r) = \sum_{j \in J} w_{ij} \cdot d_{ij}(r) ,. $$ A positive weighted disparity measure implies that officer $i$ stopped people of $r$ more often than his peers, after controlling for the locations of the stops.

Inference

An individual weighted disparity measure can be contextualize under a simulated null distribution. If officer $i$ exhibited the same behavior as his peers, then we would expect him to stop people of race $r$ in the same proportion as his peers, after controlling for location. Thus, our null hypothesis is that $p_{ij}(r) = p_{ij}^(r)$, and therefore: $$ \mathbb{E}[x_{ij}(r)] = 0 ,. $$ We simulate a null distribution for $w_{ij}(r)$ by taking $n_{ij}$ random draws from a binomial distribution with proportion $p_{ij}^(r)$ for each $j \in J$, and computing the resulting simulated weighted disparity measure as above. This null distribution is centered at 0, the hypothesized mean disparity. A one-side test with a small p-value provides evidence against the null hypothesis that officer $i$’s behavior is indistinguishable from that of his peers.

Example

Consider officer 9047.

stops_9047 <- summarize_officer_citations(my_officer_id = 9047)
stops_9047
#> # A tibble: 8 × 9
#>   location_name   n_0     n cites_0 cites    p_0 p_hat   alpha disparity
#>   <chr>         <int> <int>   <int> <int>  <dbl> <dbl>   <dbl>     <dbl>
#> 1 Boston        46018   248    9468    59 0.206  0.238 0.315    0.0101  
#> 2 Brighton       4609     4     531     0 0.115  0     0.00508 -0.000586
#> 3 Charlestown     836    22      78     4 0.0933 0.182 0.0280   0.00247 
#> 4 Dorchester    49605    81   25856    39 0.521  0.481 0.103   -0.00409 
#> 5 E Boston         76     5       4     0 0.0526 0     0.00635 -0.000334
#> 6 Roxbury       43297   343   18617   126 0.430  0.367 0.436   -0.0273  
#> 7 S Boston      10168    30    1843     3 0.181  0.1   0.0381  -0.00310 
#> 8 W Roxbury     17537    54    6259    24 0.357  0.444 0.0686   0.00601
sum(stops_9047$n)
#> [1] 787

According to the data, he made a total 787 stops across 8 towns. Although he stopped drivers identified as BLACK at higher rates than his colleagues in Boston, Charlestown, and West Roxbury, he stopped drivers identified as BLACK at lower rates in other towns.

Officer 9047’s weighted disparity measure is below zero, indicating that he did not stop BLACK drivers as often as his colleagues, after controlling for location.

x_ij_BLACK <- observe_officer()
x_ij_BLACK
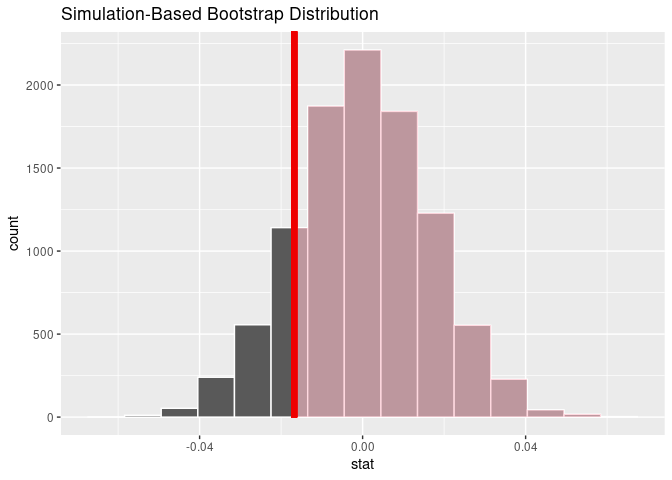
#> [1] -0.01679358

To build a null distribution for the hypothesis that officer 9047 is no different than his colleagues, we use the simulate_officer_citations() function.

sims <- simulate_officer_citations(
  n_sims = 10000, 
  my_officer_id = 9047, 
  race_of_interest = "BLACK"
)

We can then compute a p-value.

p_value_officer(sims, x_ij_BLACK)
#> # A tibble: 1 × 1
#>   p_value
#>     <dbl>
#> 1   0.843
visualize_weighted_disparity(sims, x_ij_BLACK)

References

VanDerwerken, Douglas N., Mary Fowler, and Joseph B. Kadane. 2023. “Making the Case of Racial Profiling: Opportunities for Statisticians in Legal Statistics.” To Be Submitted, 1–12.