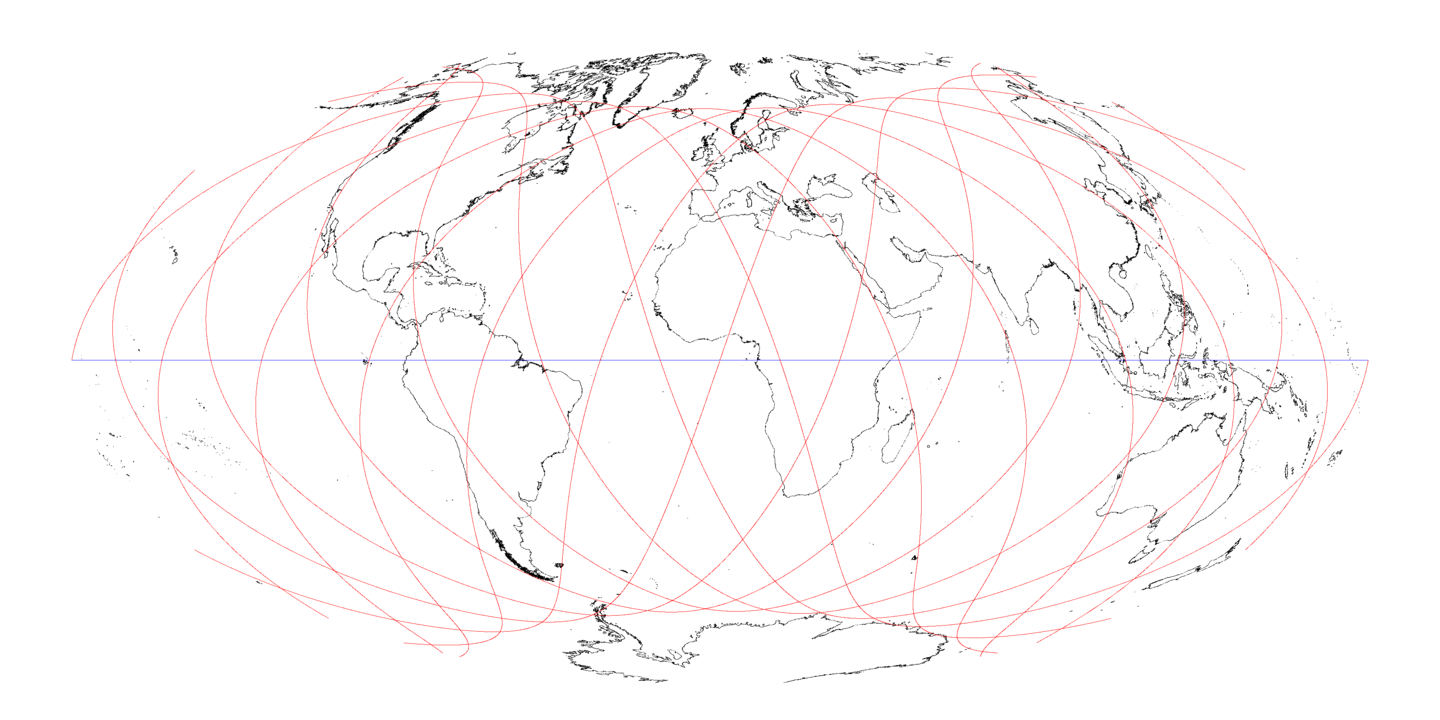
I would like a ground track of Wernher von Braun's 1952 Space Station from Across the Space Frontier. It's in a 1075 mile high, circular orbit inclined at 66.5° to the equator.
The interesting thing about a ground track is that the satellite's orbit is stable in XYZ cartesian coordinates, but the earth rotates underneath it.
- Write a computer program to simulate a 1075 mile high, 66.5° inclined, circular orbit. See if the program is numerically stable for several days of simulated time.
- Figure out how to map (X,Y,Z) orbital positions to longitude/latitude
If the satellite is at (X,Y,Z) coords with origin at the center of
the earth, Z-axis points north, X-axis points out at 0° longitude
- longitude = math.Atan2(Y, X)
- latitude = math.Atan2(Z, √(X2 + Y2))
Using Go's
math.Atan2()should get positive latitude in northern hemisphere, negative latitude in southern hemisphere. Go'smath.Remainder()worked to keep the longitude between -180° and 180° - code
- Produce an image of a flattened-out ground track on a non-rotating earth. Map (longitude, latitude) to (X,Y) coordinates in the image.
- Produce an image of a flattened-out ground track on a rotating earth.
- code
- Go's
math.Remainder(float64, float64)pivotal
- Figure out how to do a Hammer projection of the ground track on a rotating earth.
I got Shape file coastline longitude,latitude data from:
https://www.naturalearthdata.com/downloads/10m-physical-vectors/
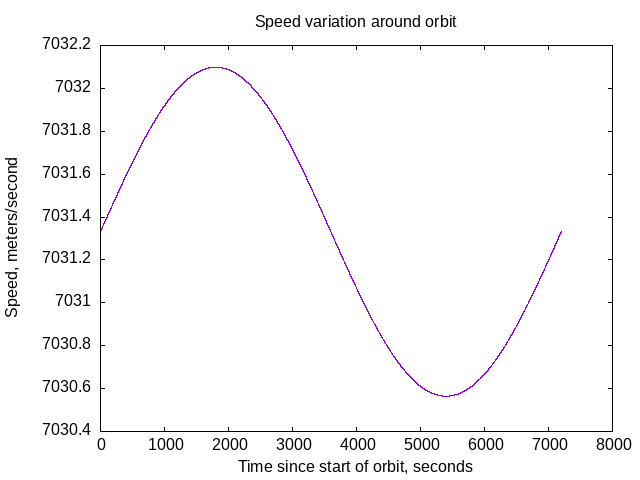
- For a circular orbit, inclined or equatorial, the magnitude of the satellite's velocity should remain constant.
A plot of the magnitude of the satellite's velocity in meters per second, versus time, for one 7200 second orbit.
Minimum speed 7030 meters/second, maximum speed 7032 meters/second. That's pretty close to constant all the way around the orbit.
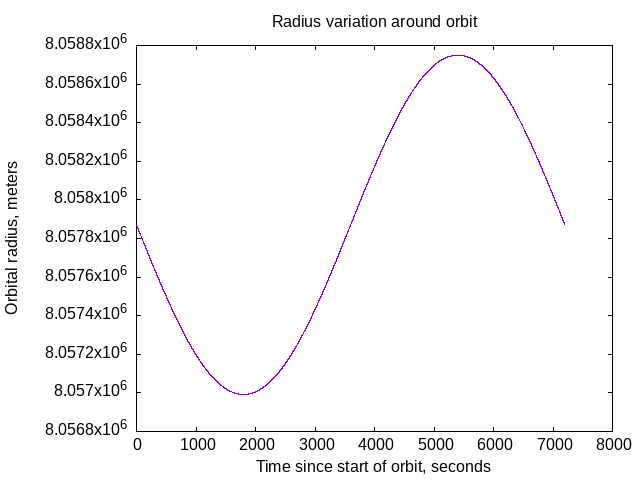
- A circular orbit should have a constant radius.
That's a plot of the satellite's distance from the origin, which is the center of the earth, in meters, versus time, for one 7200 second orbit.
Minimum radius 8058750 meters, maximum radius 8056992, a difference of 1758 meters.
I think this is an ellipse with eccentricity of 0.0002, which is pretty much a circle.
- The orbit should form a closed circle.
I used output from the circularorbit.go program.
Here's (X,Y,Z) velocity components at t=0 and t=7200
| time | Vx | Vy | Vz |
|---|---|---|---|
| 0.000 | 0.000000 | 2803.736927 | 6448.153477 |
| 7200.500 | -0.005567 | 2803.736928 | 6448.153477 |
That's so close as to be miraculous.
| time | X | Y | Z |
|---|---|---|---|
| 0.000 | 8057870.745000 | 0.000000 | 0.000000 |
| 7200.500 | 8057870.744236 | 2.543866 | 5.850492 |
After 7200.5 seconds, the satellite is 2.54 meters off in Y, 5.85 meters off in Z. This orbit is a closed circle.