This project presents a new data structure for storing ordered integer maps: a data structure that contains x->y mappings, where x and y are integers and where the lookup, assign (insert / replace), remove and iterate (in natural numeric order) operations are efficient.
The proposed data structure is a compressive, cache-friendly, radix tree that attempts to: (1) minimize the number of memory accesses required to manage the data structure, and (2) minimize the amount of memory storage required to store data. It has performance comparable to an unordered map (std::unordered_map) and is an order of magnitude faster than an ordered map (std::map).
The need to maintain an integer map arises regularly in programming. Often the integers are used to represent other entities such as symbols (e.g. a sym->sym symbolic map), file handles/descriptors (e.g. a handle->pointer file map), pointers (e.g. a pointer->pointer object map), etc. Integer maps can also be used as a building block for integer sets, floating point maps, interval maps, etc.
If the map is unordered and does not need to support a fast successor or iterate operation then usually the best data structure is a hash table employing an open addressing scheme. However there is often a need for ordered integer maps with support for a fast successor or iterate operation in natural numeric order. The obvious choice is a tree data structure such as the one provided by std::map, which unfortunately does not always have the best performance. Radix trees are an improvement and some forms of radix trees like crit-bit trees can perform better.
The proposed data structure is a radix tree that instead of using a single bit to make a decision whether to go left or right in the tree, it uses 4 bits to pick one of 16 directions. The data structure employs a compression scheme for internal pointers and stored values and is laid out in a cache-friendly manner. These properties have the effect of creating a time and space efficient data structure.
An imap is a data structure that represents an ordered 64-bit integer map. The data structure is a tree that consists of nodes, both internal and extenal. Internal nodes store the hierarchical structure of the tree and the x values. External nodes store the y values.
We first observe that a 64-bit integer written in base-16 (hexadecimal) contains 16 digits. We also observe that each digit can take one of 16 values. Thus a 64-bit integer can be written as hF...h1h0 where hi is the hexadecimal digit at position i=0,1,...,F.
An internal node consists of:
- A prefix, which is a 64-bit integer.
- A position, which is a 4-bit integer.
- 16 pointers that point to children nodes.
The prefix together with the position describe which subset from the set of 64-bit integers is contained under a particular internal node. For example, the prefix 00000000a0008000 together with position 1 is written 00000000a0008000 / 1 and describes the set of all 64-bit integers x such that 00000000a0008000 <= x <= 00000000a00080ff. In this example, position 1 denotes the highlighted digit 00000000a0008000.
In the following graphs we will use the following visual symbol to denote an internal node:
The size of an internal node is exactly 64-bytes, which happens to be the most common cache-line size. To accomplish this an internal node is stored as an array of 16 32-bit integers ("slots"). The high 28 bits of each slot are used to store pointers to other nodes; they can also be used to store the y value directly without using external node storage if the y value can "fit". The low 4 bits of each slot are used to encode one of the hexadecimal digits of the prefix. Because the lowest hexadecimal digit of every possible prefix (h0) is always 0, we use the low 4 bits of slot 0 to store the node position.
An external node consists of 8 64-bit values. Its purpose is to act as storage for y values (that cannot fit in internal node slots). The size of an external node is exactly 64-bytes.
In the following graphs we do not use an explicit visual symbol to denote external nodes. Rather we use the following visual symbol to denote a single y value:
Internal nodes with position 0 are used to encode x->y mappings, which is done as follows. First we compute the prefix of x with the lowest digit set to 0 (prfx = x & ~0xfull). We also compute the "direction" of x at position 0 (dirn = x & 0xfull), which is the digit of x at position 0. The x->y mapping is then stored at the node with the computed prefix with the y value stored in the slot pointed by the computed direction. (The y value can be stored directly in the slot if it fits, or it can be a pointer to storage in an external node if it does not.)
For example, the mapping x=A0000056->y=56 will be encoded as:
If we then add the mapping x=A0000057->y=57:
Internal nodes with position greater than 0 are used to encode the hierarchical structure of the tree. Given the node prefix and the node position, they split the subtree with the given prefix into 16 different directions at the given position.
For example, if we also add x=A0008009->y=8009:
Here the 00000000a0000000 / 3 node is the root of the subtree for all x such that 00000000a0000000 <= x <= 00000000a000ffff. Notice that the tree need not contain nodes for all positions, but only for the positions where the stored x values differ.
Slots are 32-bit integers used to encode node and y value information, but also information such as node prefix and position. The lower 4 bits of every slot are used to encode the node prefix and position; this leaves the higher 28 bits to encode node pointer and y value information.
This means that there is a theoretical upper bound of 228=268435456 to the number of x->y mappings that can be stored in the tree. However the particular implementation in this project uses one slot bit to differentiate between internal and external nodes and one slot bit to denote if a slot contains the y value directly (i.e. without external storage). This brings the theoretical upper bound down to 226=67108864.
This data structure attempts to minimize memory accesses and improve performance:
- The tree is compressed along the position axis and only nodes for positions where the stored x values differ are kept.
- The y values are stored using a compression scheme, which avoids the need for external node storage in many cases, thus saving an extra memory access.
- The tree nodes employ a packing scheme so that they can fit in a cache-line.
- The tree nodes are cache-aligned.
Notice that tree nodes pack up to 16 pointers to other nodes and that we only have 28 bits (in practice 26) per slot to encode pointer information. This might work on a 32-bit system, but it would not work well on a 64-bit system where the address space is huge.
For this reason this data structure uses a single contiguous array of nodes for its backing storage that is grown (reallocated) when it becomes full. This has many benefits:
- Node pointers are now offsets from the beginning of the array and they can easily fit in the bits available in a slot.
- Node allocation from the array can be faster than using a general memory allocation scheme like
malloc. - If care is taken to ensure that the allocated array is cache-aligned, then all node accesses are cache-aligned.
- Spatial cache locality is greatly improved.
The lookup algorithm finds the slot that is mapped to an x value, if any.
imap_slot_t *imap_lookup(imap_node_t *tree, imap_u64_t x)
{
imap_node_t *node = tree; // (1)
imap_slot_t *slot;
imap_u32_t sval, posn = 16, dirn = 0; // (1)
for (;;)
{
slot = &node->vec32[dirn]; // (2)
sval = *slot; // (2)
if (!(sval & imap__slot_node__)) // (3)
{
if ((sval & imap__slot_value__) && imap__node_prefix__(node) == (x & ~0xfull))
{ // (3.1)
IMAP_ASSERT(0 == posn); // (3.1)
return slot; // (3.1)
}
return 0; // (3.2)
}
node = imap__node__(tree, sval & imap__slot_value__); // (4)
posn = imap__node_pos__(node); // (4)
dirn = imap__xdir__(x, posn); // (5)
}
}- Set the current node to the root of the tree. The header node in the tree contains general data about the data structure including a pointer to the root node; it is laid in such a manner so that algorithms like lookup, etc. can access it as if it was a regular internal node, which avoids special casing code.
- Given a direction (
dirn) access the slot value from the current node. - If the slot value is not a pointer to another node, then:
- If the slot has a value and if the node prefix matches the x value then return the found slot.
- Otherwise return null.
- Compute the new current node and retrieve its position (
posn). - Compute the direction at the node's position from the x value and loop back to (2).
The lookup algorithm will make 16+2=18 lookups in the worst case (no more than 16 lookups to walk the tree hierarchy + 1 lookup for the tree node + 1 lookup for the y value if it is greater or equal to 226). In practice it will do far fewer lookups.
For example to lookup the value x=A0008009:
The assign algorithm finds the slot that is mapped to an x value, or inserts a new slot if necessary.
imap_slot_t *imap_assign(imap_node_t *tree, imap_u64_t x)
{
imap_slot_t *slotstack[16 + 1];
imap_u32_t posnstack[16 + 1];
imap_u32_t stackp, stacki;
imap_node_t *newnode, *node = tree; // (1)
imap_slot_t *slot;
imap_u32_t newmark, sval, diff, posn = 16, dirn = 0; // (1)
imap_u64_t prfx;
stackp = 0;
for (;;)
{
slot = &node->vec32[dirn]; // (2)
sval = *slot; // (2)
slotstack[stackp] = slot, posnstack[stackp++] = posn; // (2)
if (!(sval & imap__slot_node__)) // (3)
{
prfx = imap__node_prefix__(node); // (3.1)
if (0 == posn && prfx == (x & ~0xfull)) // (3.2)
return slot; // (3.2)
diff = imap__xpos__(prfx ^ x); // (3.3)
for (stacki = stackp; diff > posn;) // (3.4)
posn = posnstack[--stacki]; // (3.4)
if (stacki != stackp) // (3.5)
{
slot = slotstack[stacki];
sval = *slot;
IMAP_ASSERT(sval & imap__slot_node__);
newmark = imap__alloc_node__(tree); // (3.5.1)
*slot = (*slot & imap__slot_pmask__) | imap__slot_node__ | newmark; // (3.5.1)
newnode = imap__node__(tree, newmark);
*newnode = imap__node_zero__;
newmark = imap__alloc_node__(tree); // (3.5.2)
newnode->vec32[imap__xdir__(prfx, diff)] = sval; // (3.5.3)
newnode->vec32[imap__xdir__(x, diff)] = imap__slot_node__ | newmark;// (3.5.3)
imap__node_setprefix__(newnode, imap__xpfx__(prfx, diff) | diff); // (3.5.4)
}
else
{
newmark = imap__alloc_node__(tree); // (3.6)
*slot = (*slot & imap__slot_pmask__) | imap__slot_node__ | newmark; // (3.6)
}
newnode = imap__node__(tree, newmark); // (3.7)
*newnode = imap__node_zero__; // (3.7)
imap__node_setprefix__(newnode, x & ~0xfull); // (3.7)
return &newnode->vec32[x & 0xfull]; // (3.8)
}
node = imap__node__(tree, sval & imap__slot_value__); // (4)
posn = imap__node_pos__(node); // (4)
dirn = imap__xdir__(x, posn); // (5)
}
}- Set the current node to the root of the tree.
- Given a direction (
dirn) access the slot value from the current node and record it in a stack. - If the slot value is not a pointer to another node, then:
- Retrieve the node's prefix (
prfx). - If the node position (
posn) is zero and if the node prefix matches the x value then return the found slot. - Compute the XOR difference of the node's prefix and the x value (
diff). - Find the topmost (from the tree root) stack slot where the XOR difference is greater than the corresponding position.
- If such a slot is found, then:
- We must insert a new node with position equal to the XOR difference. Allocate space for the node and update the slot to point to it. Let us call this node ND.
- We must also insert a new node with position 0 to point to the y value. Allocate space for that node as well. Let us call this node N0. Initialization of node N0 will complete outside the if/else block.
- Initialize node ND so that one slot points to the current node and one slot points to node N0.
- Set the node ND prefix and position.
- Otherwise, if no such slot is found, then insert a new node with position 0 to point to the y value.
- Initialize new node with position 0 and set its prefix from the x value.
- Return the correct slot from the new node.
- Retrieve the node's prefix (
- Compute the new current node and retrieve its position (
posn). - Compute the direction at the node's position from the x value.
The assign algorithm may insert 0, 1 or 2 new nodes. It works similarly to lookup and attempts to find the slot that should be mapped to the x value. If the node that contains this slot already exists, then assign simply returns the appropriate slot within that node so that it can be filled ("assigned") with the y value.
For example after running assign for x=A0000057:
While traversing the tree the assign algorithm computes the XOR difference between the current node and the x value. If the XOR difference is greater than the current node's position then this means that the tree needs to be restructured by adding two nodes: one node to split the tree at the position specified by the XOR difference and one node with position 0 that will contain the slot to be filled ("assigned") with the y value.
For example after running assign for x=A0008059:
If the XOR difference is always less than or equal to the current node's position, then this means that the x value is contained in the subtree that has the current node as root. If the algorithm finds the bottom of the tree without finding a node with position 0, then it must insert a single node with position 0 that will contain the slot to be filled ("assigned") with the y value.
For example after running assign for x=A0008069:
The remove algorithm deletes the y value from the slot that is mapped to an x value. Any extraneous nodes in the path to the removed slot are also removed or merged with other nodes.
void imap_remove(imap_node_t *tree, imap_u64_t x)
{
imap_slot_t *slotstack[16 + 1];
imap_u32_t stackp;
imap_node_t *node = tree; // (1)
imap_slot_t *slot;
imap_u32_t sval, pval, posn = 16, dirn = 0; // (1)
stackp = 0;
for (;;)
{
slot = &node->vec32[dirn]; // (2)
sval = *slot; // (2)
if (!(sval & imap__slot_node__)) // (3)
{
if ((sval & imap__slot_value__) && imap__node_prefix__(node) == (x & ~0xfull))
{ // (3.1)
IMAP_ASSERT(0 == posn);
imap_delval(tree, slot); // (3.1)
}
while (stackp) // (3.2)
{
slot = slotstack[--stackp]; // (3.2.1)
sval = *slot; // (3.2.1)
node = imap__node__(tree, sval & imap__slot_value__); // (3.2.2)
posn = imap__node_pos__(node); // (3.2.2)
if (!!posn != imap__node_popcnt__(node, &pval)) // (3.2.3)
break; // (3.2.3)
imap__free_node__(tree, sval & imap__slot_value__); // (3.2.4)
*slot = (sval & imap__slot_pmask__) | (pval & ~imap__slot_pmask__); // (3.2.5)
}
return;
}
node = imap__node__(tree, sval & imap__slot_value__); // (4)
posn = imap__node_pos__(node); // (4)
dirn = imap__xdir__(x, posn); // (5)
slotstack[stackp++] = slot; // (6)
}
}- Set the current node to the root of the tree.
- Given a direction (
dirn) access the slot value from the current node. - If the slot value is not a pointer to another node, then:
- If the slot has a value and if the node prefix matches the x value then delete the y value from the slot.
- Loop while the stack is not empty.
- Pop a slot from the stack.
- Compute a node from the slot and retrieve its position (
posn). - Compare the node's "boolean" position (0 if the node's position is equal to 0, 1 if the node's position is not equal to 0) to the node's population count (i.e. the number of non-empty slots). This test determines if a node with position 0 has non-empty slots or if a node with position other than 0 has two or more subnodes. In either case break the loop without removing any more nodes.
- Deallocate the node.
- Update the slot.
- Compute the new current node and retrieve its position (
posn). - Compute the direction at the node's position from the x value.
- Record the current slot in a stack.
The remove algorithm may remove 0, 1 or 2 nodes. It works similarly to lookup and attempts to find the slot that should be mapped to the x value. If it finds such a slot then it deletes the value in it. If the position 0 node that contained the slot has other non-empty slots, then remove completes.
For example after running remove for x=A0000057:
If the position 0 node that contained the slot has no other non-empty slots, then it is removed.
For example after running remove for x=A0008069:
If the parent node of the position 0 node that contained the slot was removed and its parent node has only one other subnode, then it is also removed.
For example after running remove for x=A0008059:
The reference implementation is a single header C/C++ file named <imap.h>.
It provides the following types:
imap_node_t: The definition of internal and external nodes. An imap tree pointer is of typeimap_node_t *.imap_slot_t: The definition of a slot that contains y values. A slot pointer is of typeimap_slot_t *.imap_iter_t: The definition of an iterator.imap_pair_t: The definition of a pair of an x value and its corresponding slot. Used by the iterator interface.
It also provides the following functions:
imap_ensure: Ensures that the imap tree has sufficient memory forimap_assignoperations. The parameternspecifies how many such operations are expected. This is the only interface that allocates memory.imap_free: Frees the memory behind an imap tree.imap_lookup: Finds the slot that is mapped to a value. Returns0(null) if no such slot exists.imap_assign: Finds the slot that is mapped to a value, or maps a new slot if no such slot exists.imap_hasval: Determines if a slot has a value or is empty.imap_getval: Gets the value of a slot.imap_setval: Sets the value of a slot.imap_delval: Deletes the value from a slot. Note that usingimap_delvalinstead ofimap_removecan result in a tree that has superfluous internal nodes. The tree will continue to work correctly and these nodes will be reused if slots within them are reassigned, but it can result in degraded performance, especially for the iterator interface (which may have to skip over a lot of empty slots unnecessarily).imap_remove: Removes a mapped value from a tree.imap_locate: Locates a particular value in the tree, populates an iterator and returns a pair that contains the value and mapped slot. If the value is not found, then the returned pair contains the next value after the specified one and the corresponding mapped slot. If there is no such value the returned pair contains all zeroes.imap_iterate: Starts or continues an iteration. The returned pair contains the next value and the corresponding mapped slot. If there is no such value the returned pair contains all zeroes.
The implementation in <imap.h> can be tuned using configuration macros:
- Memory allocation can be tuned using the
IMAP_ALIGNED_ALLOC,IMAP_ALIGNED_FREE,IMAP_MALLOC,IMAP_FREEmacros. - Raw performance can be improved with the
IMAP_USE_SIMDmacro. The default is to use portable versions of certain utility functions, but theIMAP_USE_SIMDenables use of AVX2 on x86. If one further definesIMAP_USE_SIMD=512then use of AVX512 on x86 is also enabled.
The <imap.h> file is designed to be used as a single header file from both C and C++. It is also possible to split the interface and implementation; for this purpose look into the IMAP_INTERFACE and IMAP_IMPLEMENTATION macros.
This project includes implementations of an integer set in <iset.h> and an integer interval map in <ivmap.h>. Both implementations are based on the implementation of the integer map in <imap.h>.
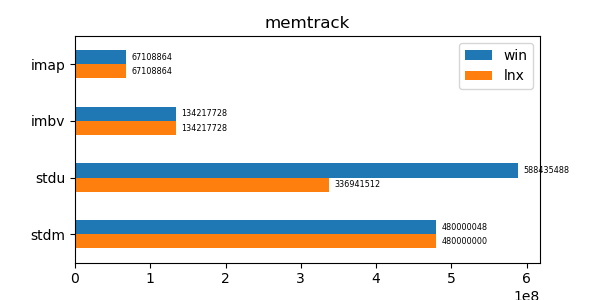
This data structure has performance comparable to an unordered map (std::unordered_map) and is an order of magnitude faster than a regular ordered map (std::map). Furthermore its memory utilization is about a third to a quarter of the memory utilization of the alternatives.
In order to determine performance and memory utilization, tests were performed on a Win11 system with WSL2 enabled. The tests were run 3 times and the smallest value was chosen as representative. Although some care was taken to ensure that the system remained idle, this is not easily possible in a modern OS.
The environments are:
- Windows:
- OS: Windows 11 22H2
- CC: Microsoft (R) C/C++ Optimizing Compiler Version 19.35.32216.1 for x64
- WSL2/Linux:
- OS: Ubuntu 20.04.6 LTS
- CC: gcc (Ubuntu 9.4.0-1ubuntu1~20.04.1) 9.4.0
The imap data structure was compiled with IMAP_USE_SIMD which enables use of AVX2. Further improvements are possible by compiling with IMAP_USE_SIMD=512 which enables use of AVX512, but this was not done in these tests as AVX512 is still not prevalent at the time of this writing.
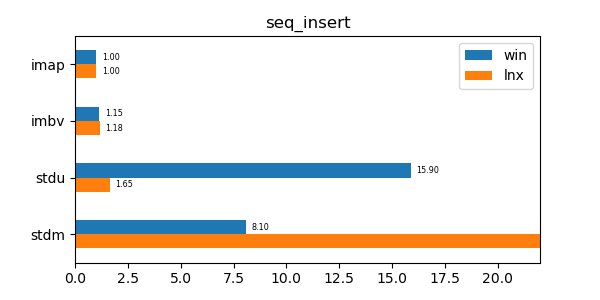
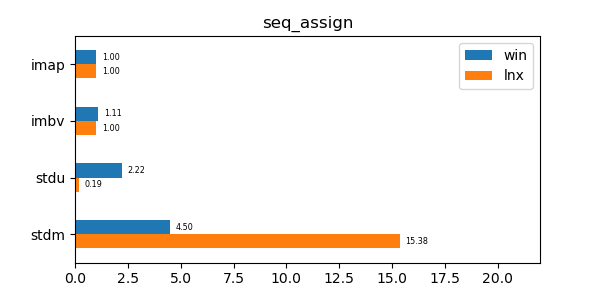
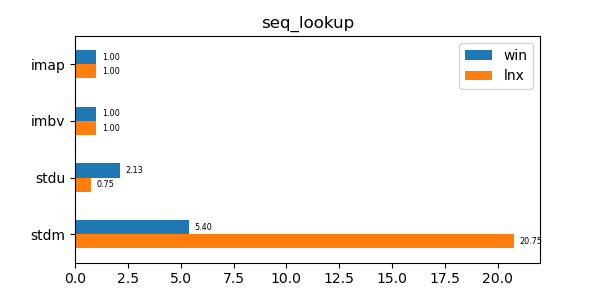
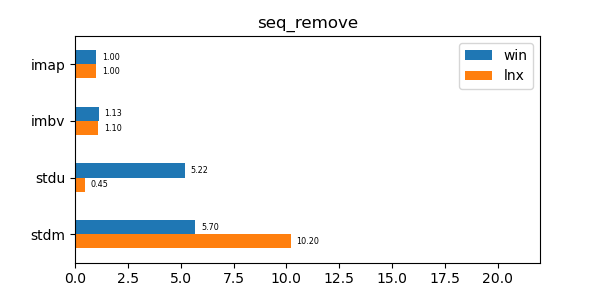
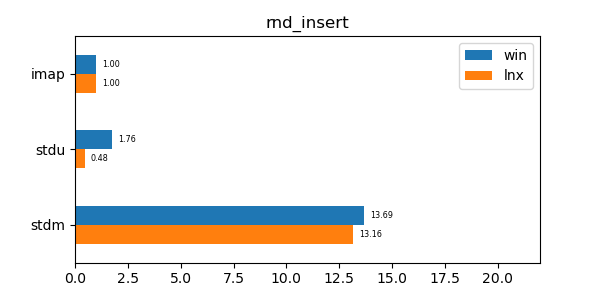
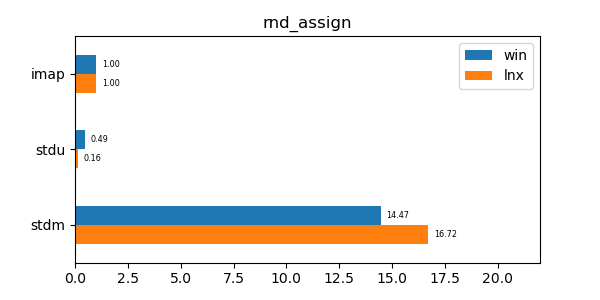
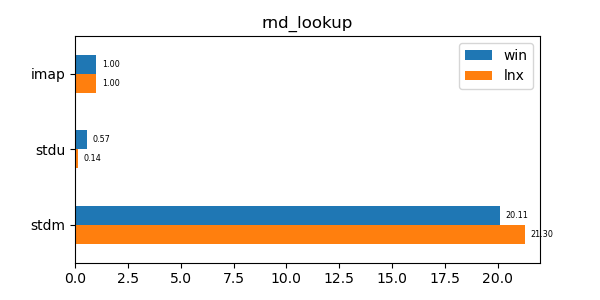
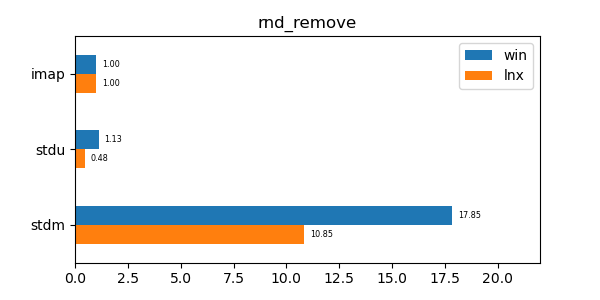
In the graphs below imap stands for the discussed data structure, imbv stands for the discussed data structure but with a modified test so that it cannot use its y value compression scheme, stdu stands for std::unordered_map and stdm stands for std::map. All times are normalized against the imap time on each system (so that the imap test "time" is always 1.0 and if a particular test took twice as much time as imap then its "time" would be 2.0). In all graphs shorter bars are better.
-
seq_insert: Insert test of 10 million sequential values. -
seq_assign: Assign test of 10 million sequential values. -
seq_lookup: Lookup test of 10 million sequential values. -
seq_remove: Remove test of 10 million sequential values. -
rnd_insert: Insert test of 10 million random values. -
rnd_assign: Assign test of 10 million random values. -
rnd_lookup: Lookup test of 10 million random values. -
rnd_remove: Remove test of 10 million random values.
MIT