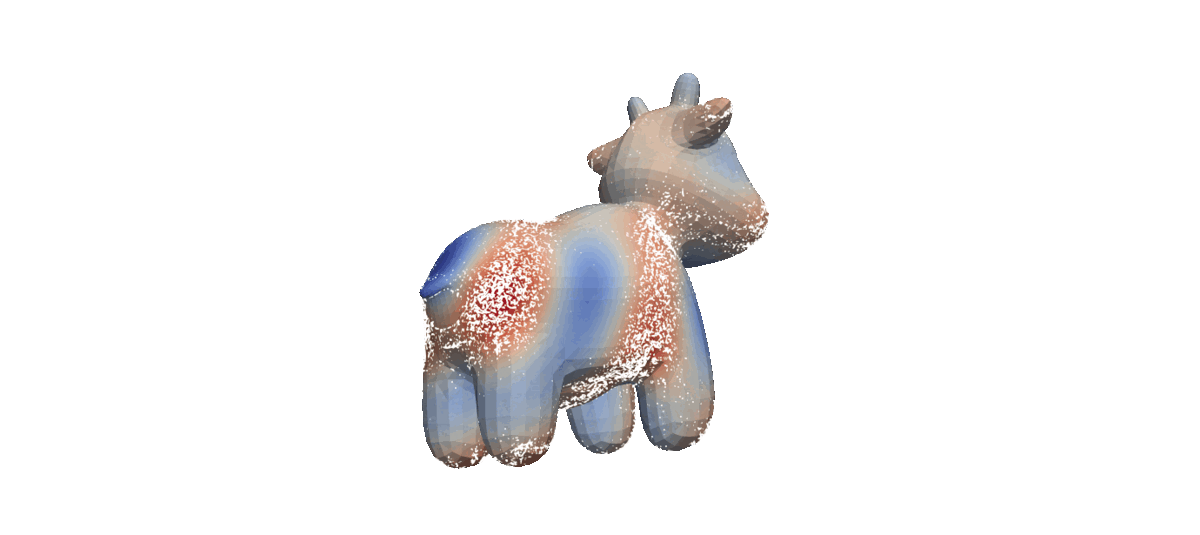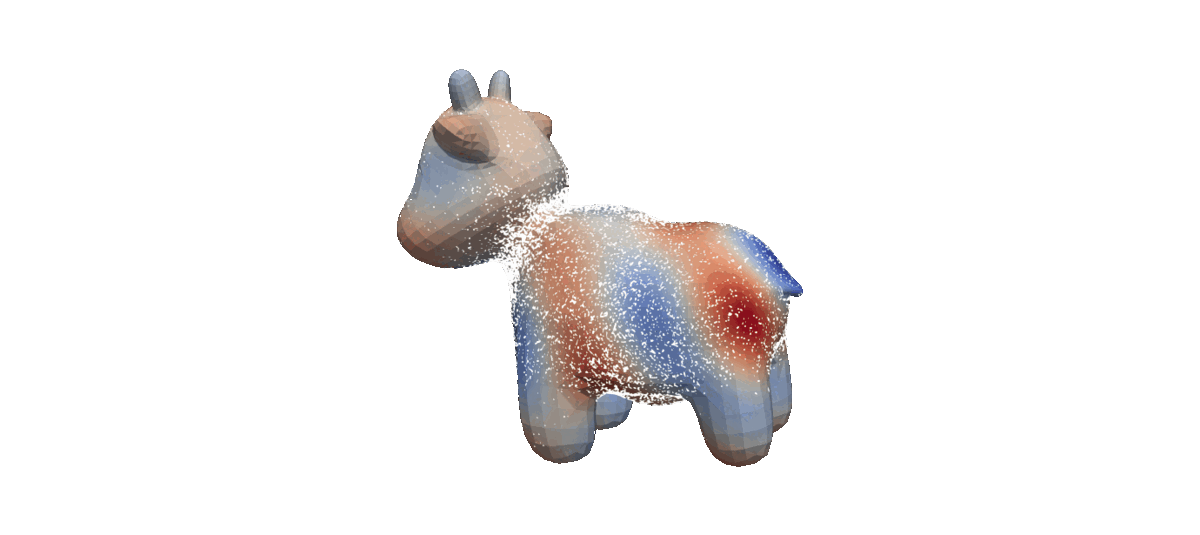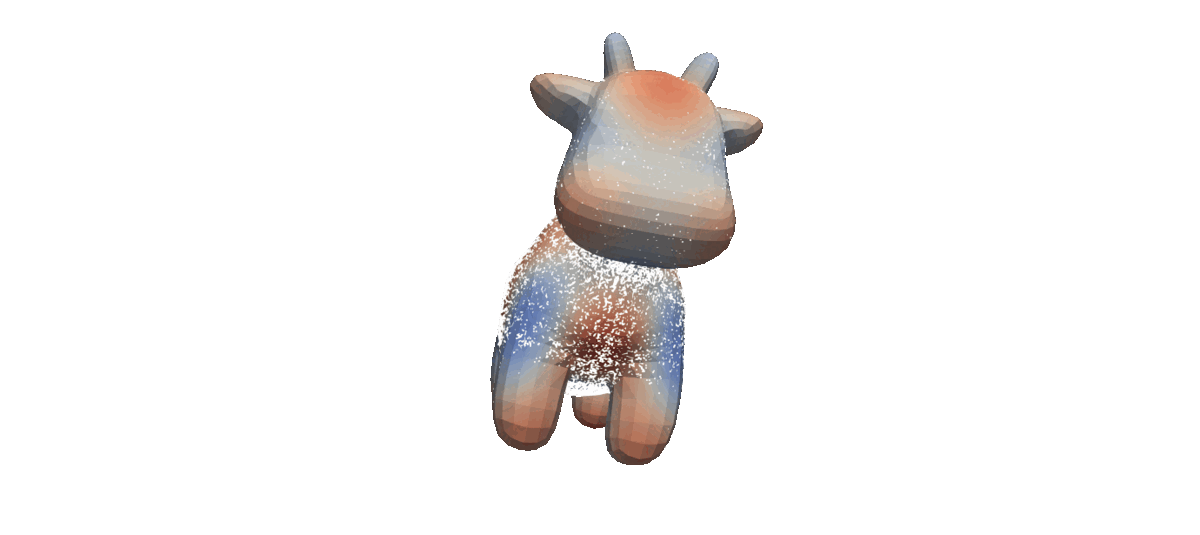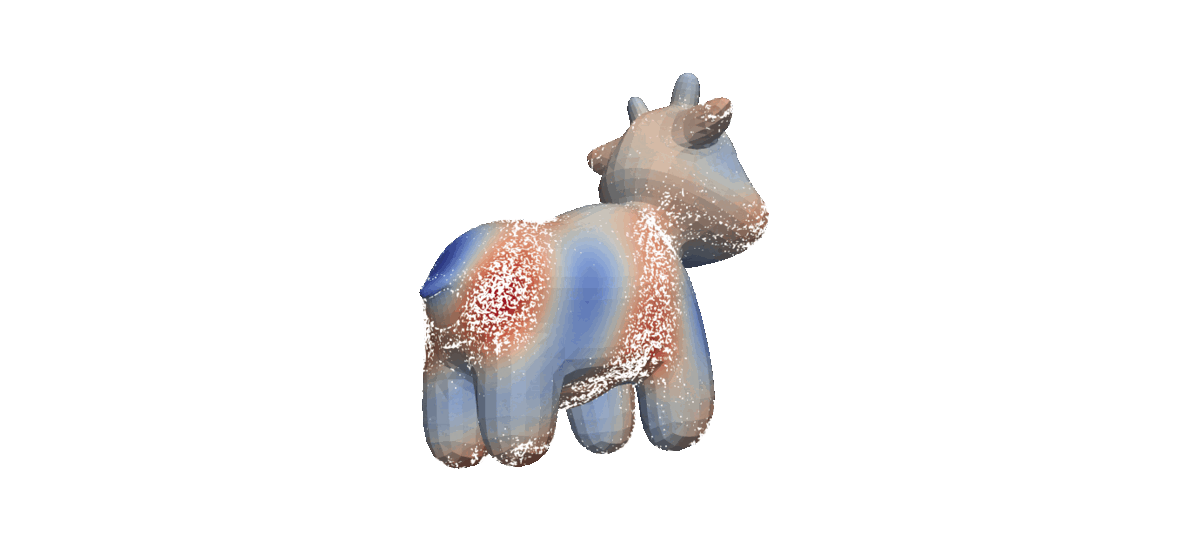
- Completely simulation-free on simple manifolds,
- Trivially applies to higher dimensions with no approximation errors,
- Tractably generalizes to general geometries!
Algorithmic comparison to related Riemanninan diffusion models:
conda env create -f environment.yml
pip install -e .
Download zip file here and uncompress into data folder.
Modify the *_datadir variables inside configs/train.yaml.
Protein data:
cd data/top500
bash batch_download.sh -f list_file.txt -p
python get_torsion_angle.py
RNA data:
cd data/rna
bash batch_download.sh -f list_file.txt -p
python get_torsion_angles.py
Mesh data:
cd data
python synthesize_mesh_data.py
The following manifolds (manifm/manifolds) are supported:
- Euclidean
- FlatTorus
- Sphere
- PoincareBall
- SPD (symmetric positive definite matrices)
- Mesh
With the only exception being Mesh, the other manifolds are "simple" (i.e., has closed-form geodesic paths).
python train.py experiment=<experiment> seed=0,1,2,3,4 -m
where <experiment> is one of the settings in configs/experiment/*.yaml.
If you find this repository helpful for your publications, please consider citing our paper:
@inproceedings{
chen2023riemannianfm,
title={Riemannian Flow Matching on General Geodesics},
author={Ricky T. Q. Chen and Yaron Lipman},
year={2023},
}
This repository is licensed under the CC BY-NC 4.0 License.