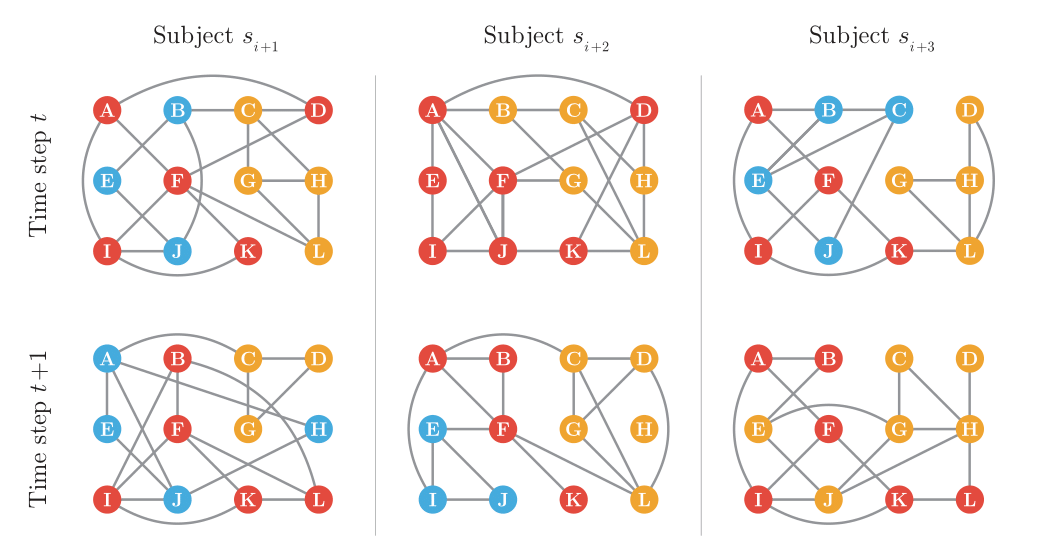
MuDCoD (Multi-subject Dynamic Community Detection) provides robust community detection in time-varying personalized networks modules. It allow signal sharing between time-steps and subjects by applying eigenvector smoothing. When available, MuDCoD leverages common signals among networks of the subjects and performs robustly when subjects do not share any apparent information. Documentation can be found here.
You can either clone the repository and crate a new virtual environment using poetry as described below, or simply use pip install mudcod.
- Clone the repository, and change current directory to
mudcod/.
git clone https://github.com/bo1929/MuDCoD.git
cd MuDCoD- Create a new virtual environment with Python version 3.9 with using any version management tool, such as
condaandpyenv.- You can use following
condacommands.
conda create -n mudcod python=3.9.0 conda activate mudcod
- Alternatively,
pyenvsets a local application-specific Python version by writing the version name to a file called.python-version, and automatically switches to that version when you are in the directory.
pyenv local 3.9.0 - You can use following
- Use poetry to install dependencies in the
mudcod/directory, and spawn a new shell.
poetry install
poetry shellSee the examples directory for simple examples of Multi-subject Dynamic DCBM, community detection with MuDCoD and cross-validation to choose alpha and beta,
For a Python interpreter to be able to import mudcod, it should be on your Python path.
The current working directory is (usually) included in the Python path.
So you can probably run the examples by running commands like python examples/community_detection.py inside the directory which you clone.
You might also want to add mudcod to your global Python path by installing it via pip or copying it to your site-packages directory.
You are able to install dependencies by using poetry install.
However, be aware that installed dependencies do not necessarily include all libraries used in experiment scripts (files in the experiments/ directory).
The goal was keeping actual dependencies as minimal as possible.
So, if you want to re-produce experiments on simulation data or on single-cell RNA-seq datasets, you need to go over the imported libraries and install them separately.
A tool like pipreqs or pigar might help in that case.
This is not the case for the examples (examples/), poetry install and/or pip install mudcod are sufficient to run them.
As described in the documentation MuDCoD takes multi-dimensional numpy arrays as the input network argument.
Hence, whether you have constructed networks separately for each subject at different time points, or if you have your networks in a different format, it is necessary to format them appropriately.
Below, we apply MuDCoD to both simulated networks and real-data networks constructed from scRNA-seq data.
To learn more about our simulation model refer to the documentation and the below section titled Multi-subject Dynamic Degree Corrected Block Model.
- First construct a
MuSDynamicDCBMinstance, i.e., simulation model, with desired parameters.
mus_dynamic_dcbm = MuSDynamicDCBM(
n=500,
k=10,
p_in=(0.2, 0.4),
p_out=(0.05, 0.1),
time_horizon=8,
num_subjects=16,
r_time=0.4,
r_subject=0.2,
)
adj_mus_dynamic, z_mus_dynamic_true = model_dcbm.simulate_mus_dynamic_dcbm(setting=1)The first dimension of numpy arrays adj_mus_dynamic and z_mus_dynamic_true is for subjects, and the second dimension is for time points.
For networks last two dimension is an z_mus_dynamic_true) last dimension is an array of
- Set some reasonable hyper-parameters.
If you have doubts, default values should work fine for
max_Kandn_iter. You can use cross-validation (seeexamples/cross_validation.py) foralphaandbeta.
T = 8
S = 16
alpha = 0.05 * np.ones((T, 2))
beta = 0.05 * np.ones(S)
max_K = 10
n_iter = 30- Run MuDCoD iterative algorithm to find smoothed spectral representations of nodes, and then predict by clustering them to communities.
pred_MuDCoD = MuDCoD(verbose=False).fit_predict(
adj_mus_dynamic,
alpha=alpha,
beta=beta,
max_K=max_K,
n_iter=n_iter,
opt_K="null",
monitor_convergence=True,
)You can compare pred_MuDCoD and z_mus_dynamic_true to evaluate the accuracy based on the Multi-subject Dynamic Degree Corrected Block Model. Note that they are both
Construction of gene co-expression networks from noisy and sparse scRNA-seq data is a challenging problem, and is itself a subject worth to conduct research on. We suggest to use Dozer [3] to filter genes and construct robust networks that will enable finding meaningful gene modules.
-
Follow the instructions and use the code snippets provided here to filter genes and construct gene co-expression networks using Dozer. It is sufficient to follow until "Section 4: Gene Centrality Analysis" (not included) for our purposes. Successfully running given code snippets will results in outputting networks (weighted, i.e., co-expression values) and other relevant information in a R data file with
.rdaextension. -
First, output networks separately for each subject at each time point. If you have
$n$ many nodes,$T$ time points and$S$ subjects; you should have$T \times S$ many$n$ by$n$ adjacency matrices. -
Collect
$T \times S$ adjacency matrices in a multi-dimensionalnumpy.arrayso that the first dimension indexes subjects and the second dimension indexes time points. Save this multi-dimensional array to disk. -
Read networks from disk with
numpy.load, and use MuDCoD as below. -
Run MuDCoD's iterative algorithm to find smoothed spectral representations of nodes, and then predict by clustering them to communities.
adj = numpy.load("/path/to/adj")
pred_comm = MuDCoD(verbose=False).fit_predict(
adj,
alpha=0.05 * np.ones((adj.shape[1], 2)),
beta=0.05 * np.ones(adj.shape[0]),
max_K=50,
n_iter=30,
opt_K="null",
monitor_convergence=True,
)There are three classes, namely DCBM, DynamicDCBM, and MuSDynamicDCBM.
We use the MuSDynamicDCBM class to generate simulation networks with a given parameter configuration.
For example, you can initialize a class instance as below.
mus_dynamic_dcbm = MuSDynamicDCBM(
n=500,
k=10,
p_in=(0.2, 0.4),
p_out=(0.05, 0.1),
time_horizon=8,
r_time=0.4,
num_subjects=16,
r_subject=0.2,
seed=0
)This will initialize a multi-subject dynamic degree corrected block model with r_subject=0.2 parameterize the degree of dissimilarity among subjects.
After initializing the MuSDynamicDCBM, we can generate an instance of multi-subject time series of networks by running the below line of code.
mus_dynamic_dcbm.simulate_mus_dynamic_dcbm(setting=setting)Different setting values correspond to the following scenarios. In our simulation experiments presented in the manuscript, we use setting=1 and setting=2.
-
setting=0: Totally independent subjects, evolve independently. -
setting=1: Subjects are siblings at the initial time step, then they evolve independently. (SSoT) -
setting=2: Subjects are siblings at each time point. (SSoS) -
setting=3: Subjects are parents of each other at time 0, then they evolve independently. -
setting=4: Subjects are parents of each other at each time point.
- [1]: Liu, F., Choi, D., Xie, L., Roeder, K. Global spectral clustering in dynamic networks. Proceedings of the National Academy of Sciences 115(5), 927–932 (2018). https://doi.org/10.1073/pnas.1718449115
- [2]: Jerber, J., Seaton, D.D., Cuomo, A.S.E. et al. Population-scale single-cell RNA-seq profiling across dopaminergic neuron differentiation. Nat Genet 53, 304–312 (2021). https://doi.org/10.1038/s41588-021-00801-6
- [3]: Lu, Shan, and Sündüz Keleş. "Debiased personalized gene coexpression networks for population-scale scRNA-seq data." Genome Research 33.6 (2023): 932-947.