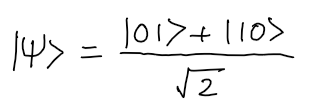/AutoBellCircuit

The Quantum Circuit automatically learns the parameters to generate a Bell State

Primary LanguagePythonGNU General Public License v3.0GPL-3.0

Bell State Circuit Generator

Submitted By: Syed Farhan Ahmad

Date of Submission: 9th September, 2020

Time of Submission: 5:30pm IST

Table of contents

Problem Statement

Implement a circuit that returns |01> and |10> with equal probability.
Requirements

  • The circuit should consist only of CNOTs, RXs and RYs.

  • Start from all parameters in parametric gates being equal to 0 or randomly chosen.

  • You should find the right set of parameters using gradient descent (you can use more advanced optimization methods if you like).

  • Simulations must be done with sampling - i.e. a limited number of measurements per iteration and noise.

  • Compare the results for different numbers of measurements: 1, 10, 100, 1000.

Instructions to Run Program

  1. Install qiskit
  2. Execute python main.py

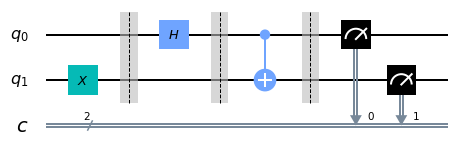
Ideal Circuit

bell state

  • The Bell State can be created by the follwing steps:
    hadamard
  • Applying H Gate to Qubit 0, and X Gate to qubit 1.
    cnot
  • Applying CNOT gate to the combination

The ideal circuit is as follows:
Ideal

Solution Architecture

  • The problem statement can be solved using a Hybrid Classical-Quantum Optimization approach.
  • The Quantum Circuit is implemented using the BellStateCircuit class in qpower_app.py.
  • The Loss function, optimizer function and backpropagation are implemented in GradientDescentOptimizer class in qpower_app.py.

architecture

Data Encoding

  1. Input data is the parameter angle_degrees, in degrees, which is the angle by which the paraterized gate will rotate.
  2. The angle is converted to radians from degrees.
  3. Data is mapped before execution using parameter_binds of the qiskit.execute function in qpower_app.py.

Parameterized Circuit

  • The parameterized circuit is created using the qiskit.ry gate, that takes angle_degrees as the input parameter.
  • Qubit 0 is initialized to statevector [1,0], and Qubit 1 to [0,1] to be able to reach the aforementioned Bell State.

Cost Function

Mean Squared Error

  • The Cost function is a simple MSE function that can easily be used with the first order derivative optimizers like Gradient Descent very easily.
  • The cost function is the squared difference of the Probability averages of both states |01> and |10>, that are obtained after the circuit is executed for a given number of shots.
    MSE

Optimizers

Gradient Descent

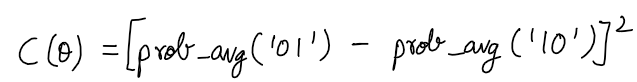
  • The Gradient Descent Optimizer is being used as it simplifies the process of loss convergence when our loss function is quadratic in nature.
  • The local and global minima are the same and the loss landscape can be easily analysed with much less compute power, and good accuracy.
  • The parameter angle_degrees is being learned, using Gradient Descent and alpha is the learning_rate.
    gd

NAG(Nesterov Accelerated Gradient)

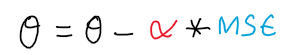
  • Coming soon

Results and Comparison

result gradient

  • The results are taken for all measurements 1, 10, 100 and 1000 respectively.
  • The error of measurement is less than 1.5% in all cases as seen.
  • Expected output: 90 degrees(or a multiple of 90 degrees)

Bonus Question

How to make sure you produce state |01> + |10> and not |01> - |10> ?

  • To prevent the occurrence of the state |01> - |10>, we will have to alter our cost function to be unsymmetrical. To alter the Mean Sqared error, we can remove the squares and keep the function linear.
  • This can be done by the following:
    prob_avg_10 - (prob_avg_01+prob_avg_10)/(2)

Future Scope

  • Use of better Optimizer functions like NAG(Nesterov Accelerated Gradient)
  • Hessian based analysis of the Loss Landscapes
  • etc.