Big O notation is used to classify algorithms according to how their run time or space requirements grow as the input size grows.
- Understand how to use Big O to describe both the time and space complexity of an algorithm
- Understand how Big O notation describes how an algorithm scales, e.g. if an algorithm works with an input that has one hundred pieces of data, how will it perform with an input that has one million pieces of data?
- Understand how to calculate Big O notation
- Use Big O notation to describe the time and space complexity of different sort algorithms
- Implement different sort algorithms
- Understand the relation of Big O to the actual performance of different sort algorithms
Big O notation is used to classify algorithms (or functions or algorithms) according to how their time or space requirements grow dependent on their input.
Big O characterises functions according to their growth rates. Suppose we have functions x and y that perform completely different tasks - if they have the same growth rate (in respect to time and space), then they will be represented using the same Big O notation (the letter O is used because the growth rate of a function is also referred to as the order of the function).
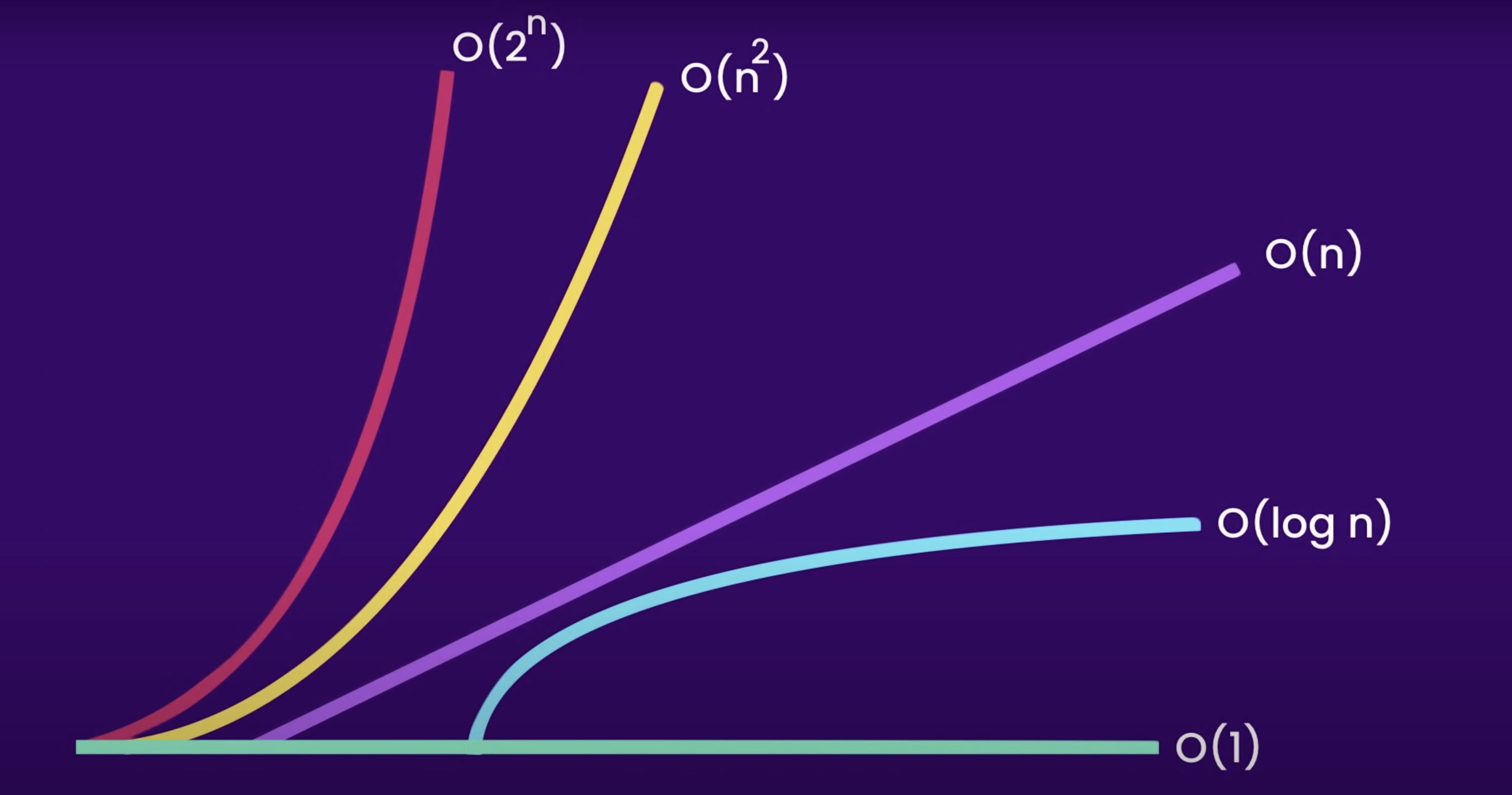
Figure 1, below, shows some commonly used Big O classifications:
Figure 1: Big O, where O(1) is the most efficient, and O(2n) the least
- O(1) - the growth is constant, no matter the input.
- O(log n) - logarithmic growth
- O(n) - linear growth
- O(n2) - quadratic growth
- O(2n) - exponential growth
The space complexity of an algorithm is the amount of memory it requires.
- O(1) - the algorithm uses a fixed (small) amount of space, irrespective of the input. For example:
const tripler = (a, b, c) => {
const x = a * b * c;
return x;
}No matter what numbers are given to tripler, it will always use the same amount of space because javascript numbers are always 64-bit floating point. Hence, tripler has space complexity of O(1).
- O(log n), O(n), O(n2) O(2n) - these indicate that the algorithm needs additional space based on the length of the input. For example:
const copier = (q) {
const copiedQ = queue();
let front = q.front;
while (front) {
copiedQ.enQueue(front.data);
front = front.next;
}
}The function copier creates a copy of the queue q. Hence, it takes O(n) space as you create n additional queued nodes (where n describes the length of q, which can vary).
The time complexity of an algorithm is the amount of time it takes to run.
- O(1) - the algorithm uses a fixed (small) amount of time, irrespective of the input. For example:
const logger = (input) => {
console.log(input)
}The function logger will always run a single console.log, no mater what the input. Hence, it has time complexity of O(1).
- O(log n), O(n), O(n2) O(2n) - these indicate that the algorithm needs additional time based on the length of the input. For example:
const sum = (stack) => {
let total = 0;
let top = stack.pop();
while (top) {
total += top.data;
top = stack.pop();
}
}The function sum sums all the numbers on the stack. Hence, it takes O(n) time as you process n additional stacked nodes (where n describes the length of the stack, which can vary).
const orderedPairs(list)
{
for (let i = 0; i < list.size; i++)
{
for (let j = 0; j < list.size; j++)
{
console.log("pair", list[i], list[j]);
}
}
}The function orderedPairs runs in O(n2) time (quadratic time), because the array has n items, so the outer loop runs n times and the inner loop runs n times for each iteration of the outer loop, giving us n2 total runs of console.log.
const fibonacci = (num) => {
if (num <= 1) return num;
return fibonacci(num - 2) + fibonacci(num - 1);
}The recursive function fibonacci has a time complexity of O(2n) (exponential time) because it's run time doubles as the input grows by 1.
When calculating complexity, throw away the constants and the least significant terms. Additionally, when summarising algorithms, only consider the worst case scenario.
Consider this:
const loopLogger = (input) => {
const mySize = 100;
for (let i = 0; i < mySize; i++) {
console.log(i)
}
for (let i = mySize - 1; i >= 0; i--) {
console.log(i)
}
}loopLogger is O(2n), which is just O(n) because the graph of 2n is still a straight line (so we have linear growth).
const anotherLogger = (list)
{
console.log("First element", list[0]);
for (int i = 1; i < list.size / 2; i++) {
console.log("First half", list[i]);
}
for (int i = 100; i > 0; i--) {
console.log("Countdown", i;
}
}anotherLogger has time complexity that is just O(n) (linear), not O(1 + n/2 + 100), because again, if you were to graph 1 + n/2 + 100, you'd get a straight line.
const logThenSumPairs = (list) => {
for (let i = 0; i < list.size; i++) {
console.log(i)
}
for (let i = 0; i < list.size; i++) {
for (let j = 0; j < list.size; j++) {
console.log("sum", list[i] + list[j]);
}
}
}The time complexity of logThenSumPairs is not O(n + n2), because we drop the least significant term, n. Hence, we have O(n2).
const isIn = (list, item) => {
for (let i = 0; i < list.size; i++) {
if (list[i] === item) return true;
}
return false;
}If isIn is lucky, the item is always the first element of the list, so it would have O(1) time complexity. However, if it is unlucky, the item will be in the last position, so it would have O(n) complexity. When generalising, it is this worst case you should consider - hence, the time complexity of isIn is O(n).
However, it is valid to be specific, too, and say that isIn has worst case complexity of O(n), and best case O(1), and thus infer some average case. Indeed, for some algorithms we can also make rigorous statements about their average case runtime. We will consider some of those later in the course.
- Fork this repository and clone the fork to your machine
- Run
npm cito install project dependencies - Implement each of the empty sort functions inside the src directory
- Add a commment to each function implementation that describes:
- Conceptually, how the sort algorithm works. You may wish to write this first, then try and implement your conceptual understanding
- The time and space complexity in Big O notation. Why does the function have that complexity?
- Add a commment to each function implementation that describes:
- Run
npm run testto test your code - Add timing results for each of your sorting algorithms into the file sortResults.md (tip:
performance.now()might be useful here, see: https://developer.mozilla.org/en-US/docs/Web/API/Performance/now). Which ran fastest? And slowest? Given your understanding of Big O complexity of the different sorting algorithms, described in Step 3., above, were those results what you expected? If not, why not? Add that summary to the file, too