Stochastic simulations
Stochastic simulations using Octave for normal multivariate and queueing theory problems.
Table of Contents
About The Project
The projects are intended for making stochastic simulations using Octave for normal multivariate and queueing theory problems.
Queueing Theory
We have a M/M/c/K/FIFO queue, with arrival rate 
We will have to make a transition rate matrix with the following idea:
With the simulation we can see 2 servers are more than enough.
Random Normal Multivariate
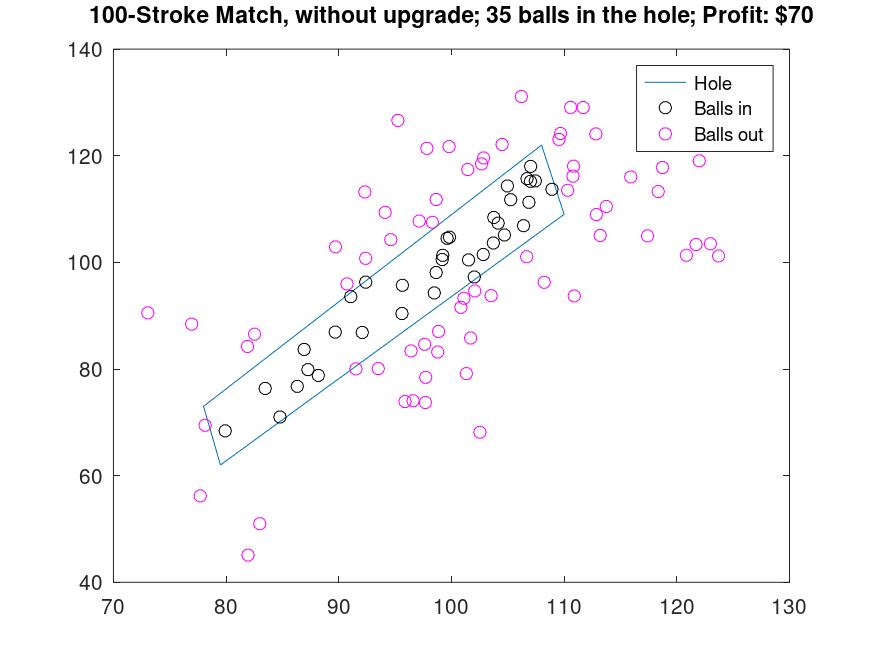
Decide if it is worth the $100.00 upgrade to play a match in which you attempt 100 'shots', and each ball that lands in the hole generates $2.00.
Make a thousand simulations of the "100-stroke match" for the robot without upgrade and calculate the average profit, then repeat for the robot with upgrade. Compare the profits and decide if it is worth the upgrade to play a match.
The strokes' position follows a normal multivariate distribution which we have the following covariance matrices:
Robot without upgrade -
Robot with upgrade -
The hole is the polygon with the following coordinates:
Without the upgrade a 100-stroke could be like this:
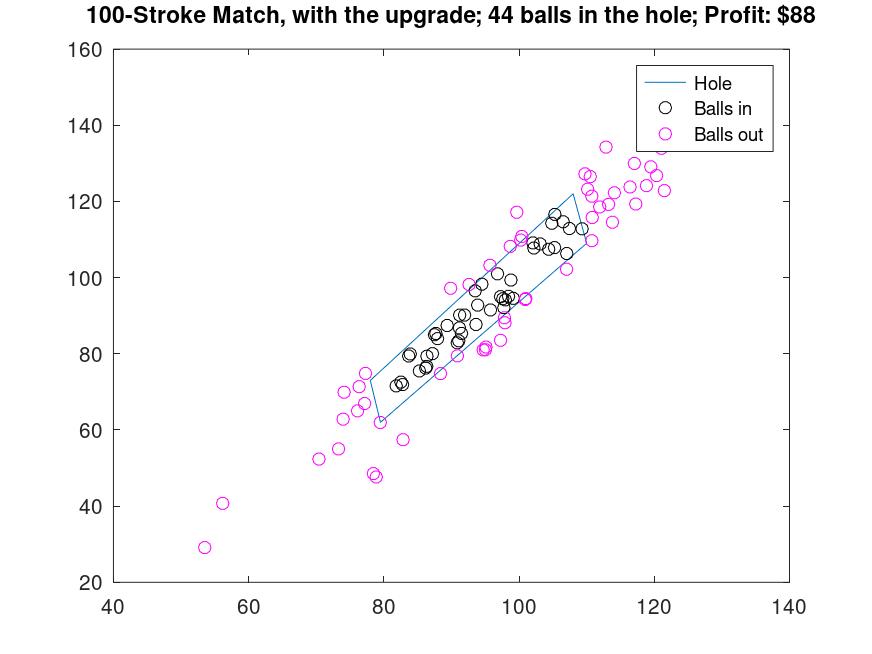
And with the upgrade:
Making the simulation we can see the upgrade is too costly, and it's better to not do it, having a better profit.
Getting Started
To get a local copy up and running follow these simple steps.
Prerequisites
Octave with the Statistics Package from Octave Forge.
Installation
- Clone the repo
git clone https://github.com/brenoslivio/Octave-Simulations.git
- Run with Octave the proper codes.
License
Distributed under the MIT License. See LICENSE for more information.