Brian D. Richardson
Installation of mismex from GitHub requires the
devtools
package and can be done with the following code:
## install the package
devtools::install_github(repo = "brian-d-richardson/mismex",
ref = "main")## load the package
library(mismex)
## load additional packages
library(MASS)
library(dplyr)
library(tidyverse)
library(ggplot2)The mismex package contains functions to estimate causal effects in
the presence of confounding and a mismeasured exposure. The methods
implemented are introduced in the paper, “Addressing confounding and
continuous exposure measurement error using corrected score functions,”
which is currently in progress.
An example of the three proposed estimators (g-formula, IPW, and doubly robust) used on a simulated data set is provided below.
Data are generated below according to the data generation process described in the third simulation study:
- sample size
$n=2000$ , - two independent confounders
$L_1 \sim \textrm{Bernoulli}(0.5), L_2 \sim N(1, 0.5)$ - univariate exposure
$A$ , where$A|\pmb{L} \sim N(2 + 0.9L_1 - 0.6L2, 1.1)$ - continuous outcome
$Y$ , with$Y|\pmb{L},A \sim N(1.5 + 0.7A + 0.9L_1 - 0.7L_2 + - 0.6AL_1 + 0.4AL_2, 0.16)$ - resulting MSM
$\textrm{E}{Y(a)} = \gamma_0 + \gamma_1a$ , where$\pmb{\gamma} = (\gamma_0, \gamma_1) = (1.35, 0.75)$ - mismeasured exposure
$A^* = A + \epsilon$ , where$\epsilon \sim N(0, 0.16)$
## define parameters
n = 2000 # sample size
seed = 1 # random number seed
mc.seed <- 123 # MCCS seed
cov.e <- 0.16 # var(epsilon)
inv.link <- inv.ident # inverse link
d.inv.link <- d.inv.ident # derivative of inverse link
g <- c(1.5, 0.7, 0.9, -0.6, -0.7, 0.4) # outcome model parameters
formula <- "~A*L1 + A*L2" # outcome model formula
ps.formula <- "~L1 + L2" # propensity score model formula
ipw.formula <- "~A" # MSM formula## generate data
set.seed(seed)
L1 <- rbinom(n, 1, 0.5) # confounder 1
L2 <- rnorm(n, 1, sqrt(0.5)) # confounder 2
A <- rnorm(n, 2 + 0.9*L1 - 0.6*L2, sqrt(1.1)) # exposure
a <- seq(min(A), max(A), length = 4) # grid of exposures
EY <- inv.link(model.matrix(as.formula(formula)) %*% g) # mean of outcome
Y <- rnorm(n, EY, sqrt(0.16)) # outcome
Astar <- A + rnorm(n, 0, sqrt(cov.e)) # mismeasured A
datstar <- data.frame(Y, A = Astar, L1, L2) # mismeasured data
head(datstar, 5)## Y A L1 L2
## 1 2.2186524 1.1634983 0 1.8025415
## 2 2.5664615 1.7145178 0 1.7862545
## 3 2.1174644 4.3731142 1 0.3842672
## 4 2.8111597 1.7921312 1 1.1490097
## 5 0.9702103 -0.4505236 0 1.0490701
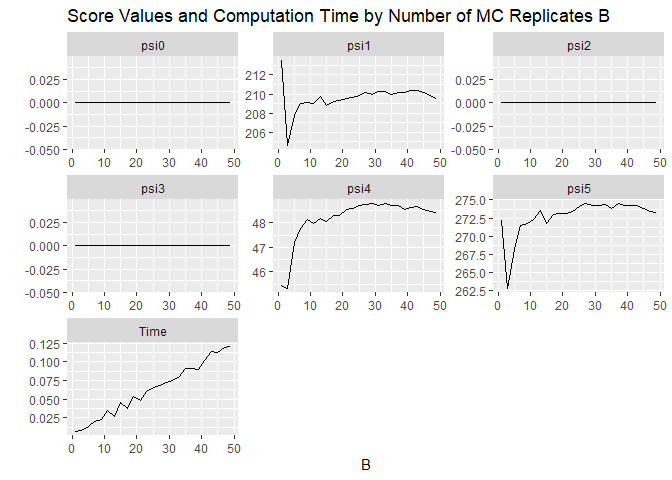
The dose response curve at chosen values of the exposure
Before fitting the model, we determine an appropriate number of
Monte-Carlo replicates
## g-formula arguments
gfmla.args <- list(formula = formula,
inv.link = inv.link,
d.inv.link = d.inv.link)
## naive estimator
gfmla.naive <- fit.glm(data = datstar,
args = gfmla.args,
return.var = F)$est
## grid of possible B values
B.grid <- seq(1, 50, by = 2)
## store psi and computation time B
B.search <- vapply(
X = 1:length(B.grid),
FUN.VALUE = numeric(8),
FUN = function(ii) {
st <- Sys.time()
get.psi.glm.mccs <- make.mccs(
get.psi = get.psi.glm, data = datstar, args = gfmla.args,
cov.e = cov.e, B = B.grid[ii], mc.seed = mc.seed)
psi <- get.psi.glm.mccs(x = gfmla.naive)
et <- Sys.time()
return(c(B = B.grid[ii],
Time = et - st,
psi = psi))
}) %>%
t() %>%
as.data.frame() %>%
`colnames<-`(c("B", "Time", paste0("psi", 0:5))) %>%
pivot_longer(cols = !B)
## plot results
ggplot(data = B.search,
aes(x = B,
y = value)) +
geom_line() +
facet_wrap(~ name,
scales = "free") +
labs(y = "") +
ggtitle("Score Values and Computation Time by Number of MC Replicates B")Based on these plots, the G-formula MCCS seems to stabilize around
The function fit.gfmla.mccs returns a list with three items: the
parameter estimates, their estimated covariance matrix, and a
bias-corrected covariance matrix estimate. Below a table is shown of
estimates and (crude and bias-corrected) standard errors.
## number of MC replicates
B <- 30
## G-formula
gfmla.res <- fit.gfmla.mccs(
data = datstar,
a = a,
cov.e = cov.e,
B = B,
mc.seed = mc.seed,
return.var = TRUE,
args = gfmla.args)
cbind(est = round(gfmla.res$est, 2),
stde = round(sqrt(diag(gfmla.res$var)), 2),
bc.stde = round(sqrt(diag(gfmla.res$bc.var)), 2))## est stde bc.stde
## g.0 1.52 0.05 0.05
## g.1 0.69 0.02 0.02
## g.2 0.88 0.05 0.05
## g.3 -0.58 0.03 0.03
## g.4 -0.70 0.02 0.02
## g.5 0.39 0.01 0.01
## EYa.1 -0.48 0.06 0.06
## EYa.2 1.57 0.02 0.02
## EYa.3 3.62 0.03 0.03
## EYa.4 5.67 0.07 0.07
Parameters
## IPW arguments
ipw.args <- list(formula = ipw.formula,
ps.formula = ps.formula,
inv.link = inv.link,
d.inv.link = d.inv.link)
## IPW estimation
ipw.res <- fit.ipw.mccs(
data = datstar,
cov.e = cov.e,
B = B,
mc.seed = mc.seed,
return.var = TRUE,
args = ipw.args)
cbind(est = round(ipw.res$est, 2),
stde = round(sqrt(diag(ipw.res$var)), 2),
bc.stde = round(sqrt(diag(ipw.res$bc.var)), 2))## est stde bc.stde
## g.0 1.78 0.19 0.21
## g.1 0.55 0.09 0.09
## coef.a.l.1 2.06 0.05 0.05
## coef.a.l.2 0.88 0.05 0.05
## coef.a.l.3 -0.66 0.04 0.04
## log.var.a.l1 0.13 0.04 0.04
Finally, we estimate outcome model parameters, propensity model
parameters, and the dose response curve using the doubly robust MCCS
method, again with
## arguments for double robust estimation
dr.args <- list(formula = formula,
ps.formula = ps.formula,
inv.link = inv.link,
d.inv.link = d.inv.link)
## Double Robust
dr.res <- fit.dr.mccs(
data = datstar,
a = a,
cov.e = cov.e,
B = B,
mc.seed = mc.seed,
return.var = TRUE,
args = dr.args)
cbind(est = round(dr.res$est, 2),
stde = round(sqrt(diag(dr.res$var)), 2),
bc.stde = round(sqrt(diag(dr.res$bc.var)), 2))## est stde bc.stde
## g.0 1.51 0.05 0.05
## g.1 0.70 0.02 0.02
## g.2 0.89 0.05 0.05
## g.3 -0.59 0.03 0.03
## g.4 -0.72 0.02 0.02
## g.5 0.40 0.02 0.02
## coef.a.l.1 2.06 0.05 0.05
## coef.a.l.2 0.88 0.05 0.05
## coef.a.l.3 -0.66 0.04 0.04
## log.var.a.l1 0.13 0.04 0.04
## EYa.1 -0.52 0.07 0.07
## EYa.2 1.56 0.02 0.02
## EYa.3 3.64 0.03 0.03
## EYa.4 5.72 0.07 0.07
Consider a new data generating process with a binary outcome and case cohort sampling:
- continuous confounder
$L \sim U(0, 1)$ , - trivariate continuous exposure
$\pmb{A} = (A_1, A_2, A_3)^T$ with$\pmb{A}|L$ having multivariate normal distribution $N_3\left(\begin{bmatrix} 0.4L \ -0.4L \ 0.2 - 0.1L \end{bmatrix}, \begin{bmatrix} 0.09 & 0 & 0 \ 0 & 0.09 & 0 \ 0 & 0 & 0.09 \end{bmatrix}\right)$, - mismeasured exposure
$\pmb{A}^* = (A^_1, A^_2, A^*_3)^T = \pmb{A} + \pmb{\epsilon}$,
where
$\pmb{\epsilon} = (\epsilon_1, \epsilon_2, \epsilon_3)^T \sim N(\pmb{0}, \pmb{\Sigma}_e)$ , $\pmb{\Sigma}_e = \begin{bmatrix} \sigma_e^2 & 0 & 0 \ 0 & \sigma_e^2 & 0 \ 0 & 0 & 0\end{bmatrix}$, - binary outcome
$Y$ with$\textrm{E}(Y|\pmb{A},L) = \widetilde\gamma_0 + \widetilde\gamma_1 a_1 + \widetilde\gamma_2 a_2 + \widetilde\gamma_3 a_3 + \widetilde\gamma_4L + \widetilde\gamma_5 a_1L + \widetilde\gamma_6 a_2L + \widetilde\gamma_7 a_3L$ , where$\widetilde{\pmb{\gamma}} = (\widetilde\gamma_0, \widetilde\gamma_1, \widetilde\gamma_2, \widetilde\gamma_3, \widetilde\gamma_4, \widetilde\gamma_5, \widetilde\gamma_6, \widetilde\gamma_7)^T = (0.4, 0.15, 0.15, 0.2, 0.1, 0.1, 0, -0.1)^T$ , - proportion
$\pi=0.25$ of cases selected to have exposure$\pmb{A}$ measured, as indicated by havingR=1.
seed <- 1 # random seed
n <- 800 # sample size
B <- 30 # MC replicates
mc.seed <- 123 # MC seed
pi.cc <- 0.25 # case-cohort proportion
gg <- c(0.4, 0.15, 0.15, 0.2,
0.1, 0.1, 0, -0.1) # Y|A,L parameters
g <- gg[1:4] + 0.5*gg[5:8] # MSM parameters
formula <- "~A1*L + A2*L + A3*L" # Y|A,L model formula
ps.formula <- "~L" # PS model formula
inv.link <- inv.ident; # MSM link function
d.inv.link <- d.inv.ident; # MSM derivative of link
vare <- 0.05 # variance of A1, A2
cov.e <- diag(c(vare, vare, 0)) # measurement error variance
coef.a.l <- matrix(
data = c(0, 0.4, 0, -0.4, 0.2, -0.1), # coefs in A|L model
nrow = 3, byrow = T)
var.a.l <- c(0.09, 0.09, 0.09) # variance of A|L
# generate data -----------------------------------------------------------
set.seed(seed) # seed for reproducibility
L <- runif(n) # confounder
A <- mvrnorm(n = n, # true exposure
mu = c(0, 0, 0),
Sigma = diag(var.a.l)) +
cbind(1, L) %*% t(coef.a.l)
colnames(A) = paste0("A", 1:3)
Astar <- A + mvrnorm(n = n, # mismeasured exposure
m = c(0, 0, 0),
Sigma = cov.e)
Y_prob <- cbind(1, A, L, A*L) %*% gg # mean of binary outcome
Y_prob[Y_prob < 0] <- 0 # correct Y_prob in rare cases
Y_prob[Y_prob > 1] <- 1
Y <- rbinom(n, 1, Y_prob) # binary outcome
colnames(A) <- colnames(Astar) <-
c("A1", "A2", "A3")
R <- rbinom(n, 1, pi.cc) # c-c sampling
A[R == 0 & Y == 0] <-
Astar[R == 0 & Y == 0] <- NA
datstar <- data.frame(Y, Astar, L, R) # mismeasured data
a <- apply(A, 2, function(x) # exposure values of interest
quantile(x, c(0.25, 0.5, 0.75), na.rm = T))
colnames(a) <- colnames(A)
args <- list(formula = formula, # arguments for fitting
ps.formula = ps.formula,
inv.link = inv.link,
d.inv.link = d.inv.link)To account for case cohort sampling, we add a sampling weight variable
cc.wts to the data set, given by
$\frac{(1-Y)R}{\widehat{pi}{cc}} + Y$, where
$\widehat{pi}{cc} = \sum_i \frac{R_i(1-Y_i)}{1-Y_i}$.
## estimate case-cohort weights
pi.cc.hat <- mean(datstar$R[datstar$Y == 0])
datstar$cc.wts <- (1 - datstar$Y) * datstar$R / pi.cc.hat + Y
## corrected doubly robust estimator
dr.cc.mccs <- fit.dr.mccs(data = datstar, args = args, a = a,
cov.e = cov.e, B = B, mc.seed = mc.seed)
cbind(est = round(dr.cc.mccs$est, 2),
stde = round(sqrt(diag(dr.cc.mccs$var)), 2),
bc.stde = round(sqrt(diag(dr.cc.mccs$bc.var)), 2))## est stde bc.stde
## g.0 0.26 0.09 0.10
## g.1 0.42 0.31 0.34
## g.2 0.22 0.20 0.22
## g.3 -0.01 0.40 0.44
## g.4 0.53 0.19 0.22
## g.5 -0.20 0.55 0.62
## g.6 -0.10 0.63 0.71
## g.7 -0.64 0.39 0.46
## coef.a.l.1 0.02 0.05 0.05
## coef.a.l.2 0.02 0.04 0.04
## coef.a.l.3 0.17 0.04 0.04
## coef.a.l.4 0.39 0.08 0.08
## coef.a.l.5 -0.42 0.07 0.08
## coef.a.l.6 -0.07 0.06 0.06
## log.var.a.l1 -2.41 0.12 0.12
## log.var.a.l2 -2.33 0.11 0.11
## log.var.a.l3 -2.31 0.08 0.08
## EYa.1 0.39 0.06 0.06
## EYa.2 0.48 0.04 0.04
## EYa.3 0.59 0.06 0.06
The application code uses publicly available files from the HVTN 505 trial. To get the data files (called at the top of “application_revised.R”), first go to Start Page: /HVTN Public Data/HVTN 505 (scharp.org). Next, navigate to the folder “correlates analysis” and download the tar.gz located there. After download, this can be installed locally by running “R CMD INSTALL HVTN505_2019-08-08.tar.gz” in the Terminal or by running ‘devtools::install_local(“HVTN505_2019-4-25.tar.gz”)’. This will include the necessary data object “dat.505.rda”. Then navigate back to the parent folder (same url as before) and into the Fong et al. folder, where the other data file “primary505_for_sharing_upd.csv” can be downloaded directly.