DiffEqFlux.jl

DiffEqFlux.jl fuses the world of differential equations with machine learning by helping users put diffeq solvers into neural networks. This package utilizes DifferentialEquations.jl and Flux.jl as its building blocks to support research in Scientific Machine Learning and neural differential equations in traditional machine learning.

Problem Domain

DiffEqFlux.jl is not just for neural ordinary differential equations. DiffEqFlux.jl is for neural differential equations. As such, it is the first package to support and demonstrate:

Stiff neural ordinary differential equations (neural ODEs)
Neural stochastic differential equations (neural SDEs)
Neural delay differential equations (neural DDEs)
Neural partial differential equations (neural PDEs)
Neural jump stochastic differential equations (neural jump diffusions)
Hybrid neural differential equations (neural DEs with event handling)

with high order, adaptive, implicit, GPU-accelerated, Newton-Krylov, etc. methods. For examples, please refer to the release blog post. Additional demonstrations, like neural PDEs and neural jump SDEs, can be found at this blog post (among many others!).

Do not limit yourself to the current neuralization. With this package, you can explore various ways to integrate the two methodologies:

Neural networks can be defined where the “activations” are nonlinear functions described by differential equations.
Neural networks can be defined where some layers are ODE solves
ODEs can be defined where some terms are neural networks
Cost functions on ODEs can define neural networks

Citation

If you use DiffEqFlux.jl or are influenced by its ideas for expanding beyond neural ODEs, please cite:

@article{DBLP:journals/corr/abs-1902-02376,
  author    = {Christopher Rackauckas and
               Mike Innes and
               Yingbo Ma and
               Jesse Bettencourt and
               Lyndon White and
               Vaibhav Dixit},
  title     = {DiffEqFlux.jl - {A} Julia Library for Neural Differential Equations},
  journal   = {CoRR},
  volume    = {abs/1902.02376},
  year      = {2019},
  url       = {http://arxiv.org/abs/1902.02376},
  archivePrefix = {arXiv},
  eprint    = {1902.02376},
  timestamp = {Tue, 21 May 2019 18:03:36 +0200},
  biburl    = {https://dblp.org/rec/bib/journals/corr/abs-1902-02376},
  bibsource = {dblp computer science bibliography, https://dblp.org}
}

Example Usage

For an overview of what this package is for, see this blog post.

Optimizing parameters of an ODE

First let's create a Lotka-Volterra ODE using DifferentialEquations.jl. For more details, see the DifferentialEquations.jl documentation

using DifferentialEquations
function lotka_volterra(du,u,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = α*x - β*x*y
  du[2] = dy = -δ*y + γ*x*y
end
u0 = [1.0,1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(lotka_volterra,u0,tspan,p)
sol = solve(prob,Tsit5())
using Plots
plot(sol)

Next we define a single layer neural network that uses the diffeq_adjoint layer function that takes the parameters and returns the solution of the x(t) variable. Note that the diffeq_adjoint is usually preferred for ODEs, but does not extend to other differential equation types (see the performance discussion section for details). Instead of being a function of the parameters, we will wrap our parameters in param to be tracked by Flux:

using Flux, DiffEqFlux
p = param([2.2, 1.0, 2.0, 0.4]) # Initial Parameter Vector
params = Flux.Params([p])

function predict_adjoint() # Our 1-layer neural network
  diffeq_adjoint(p,prob,Tsit5(),saveat=0.0:0.1:10.0)
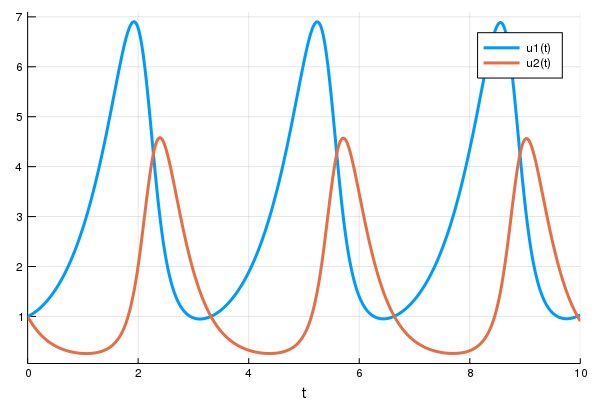
end

Next we choose a loss function. Our goal will be to find parameter that make the Lotka-Volterra solution constant x(t)=1, so we defined our loss as the squared distance from 1:

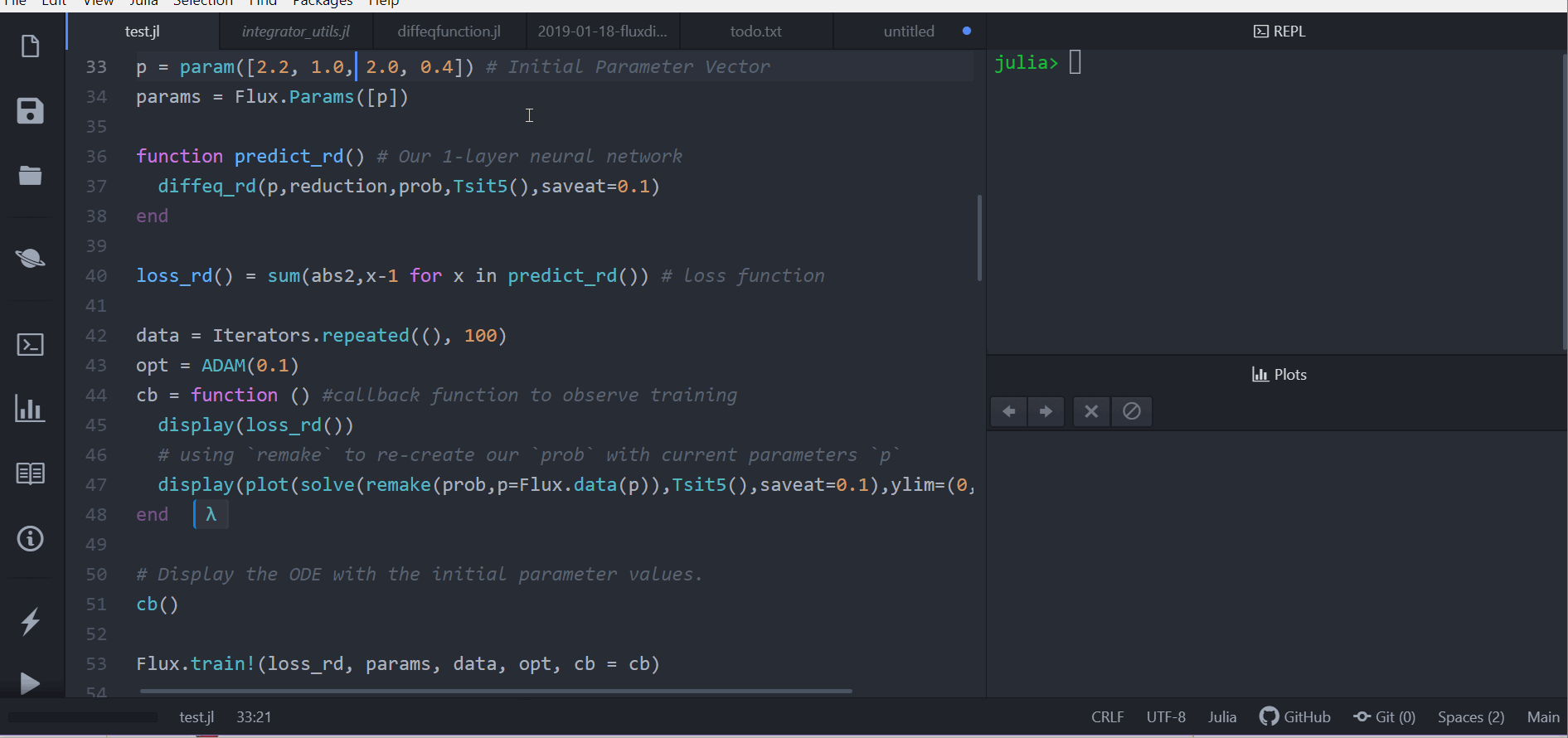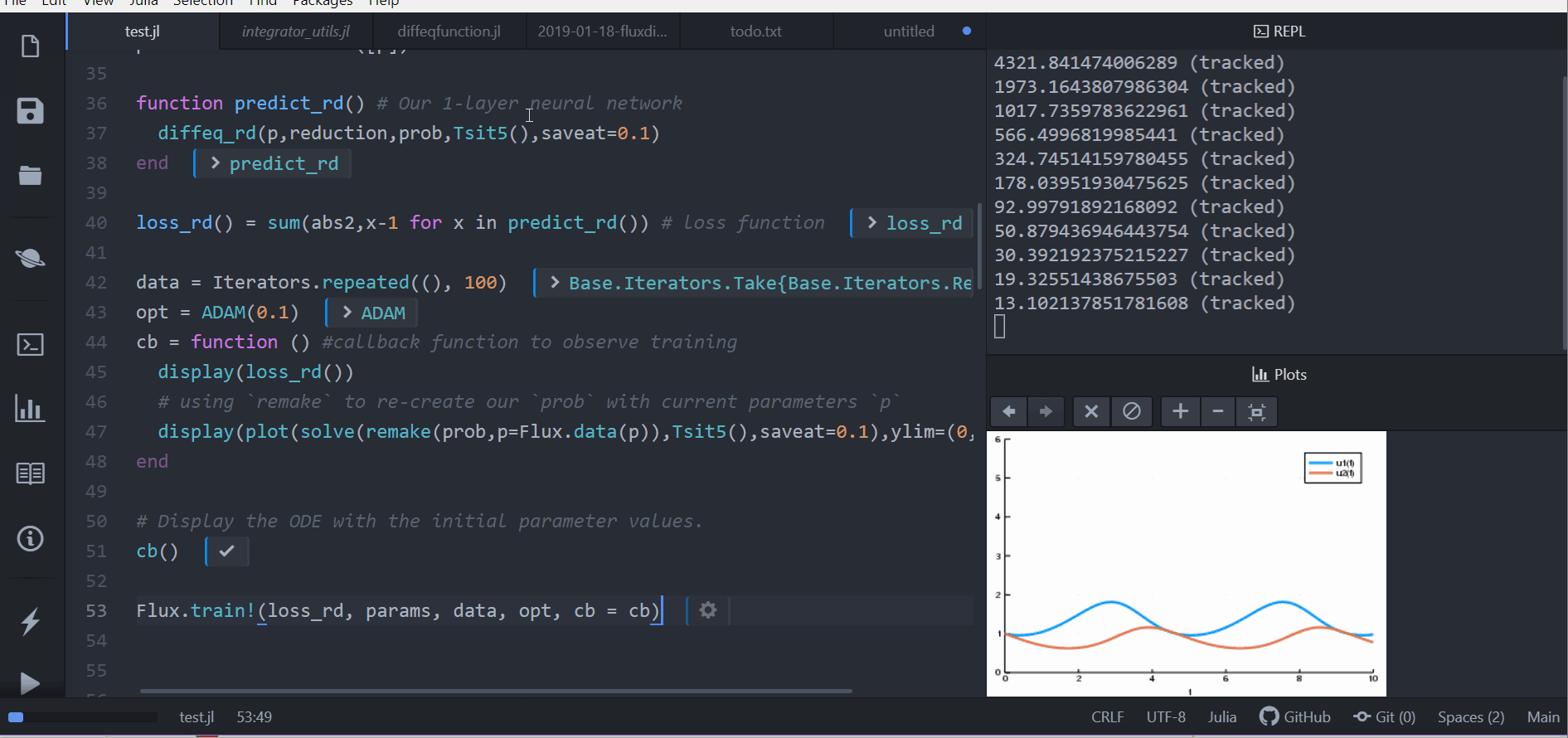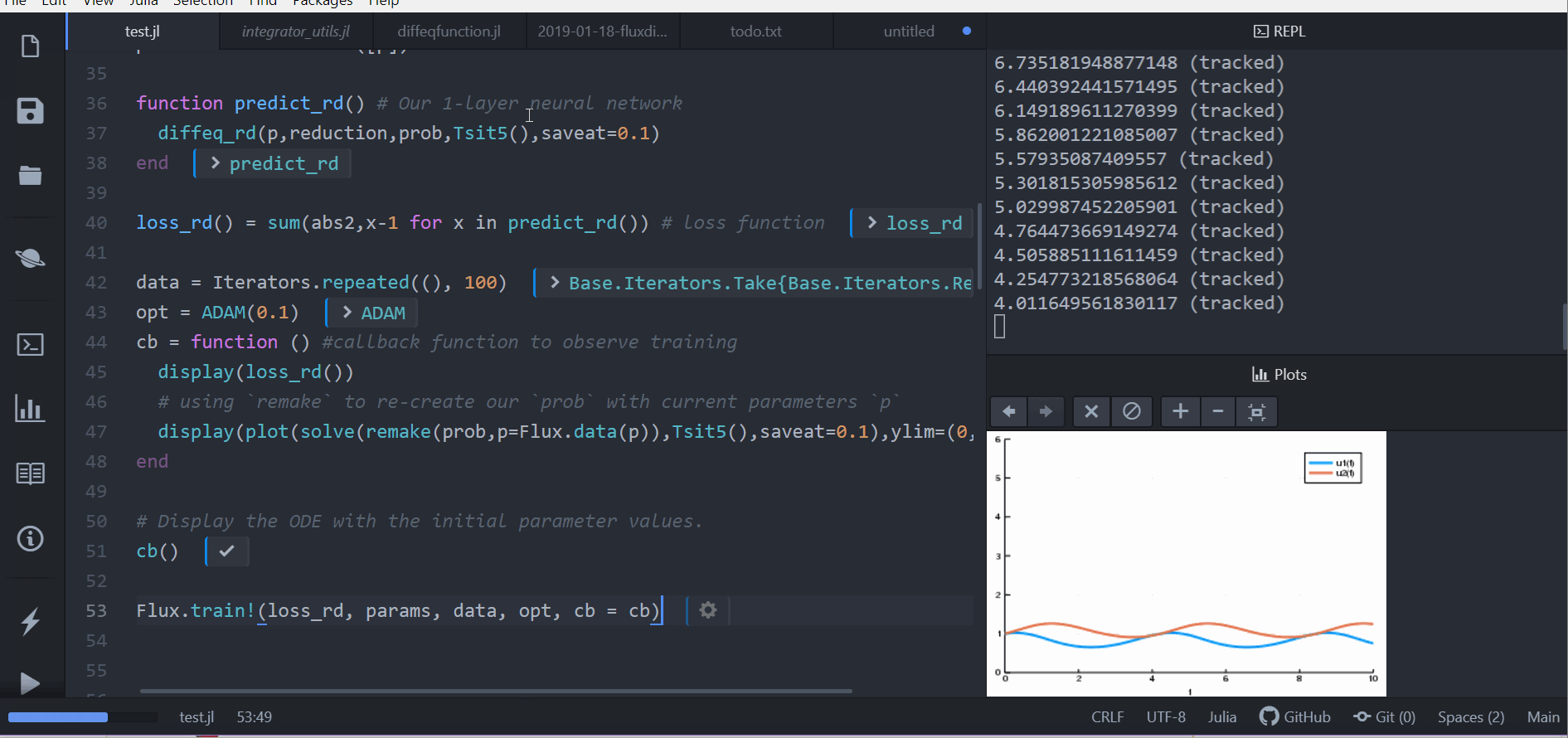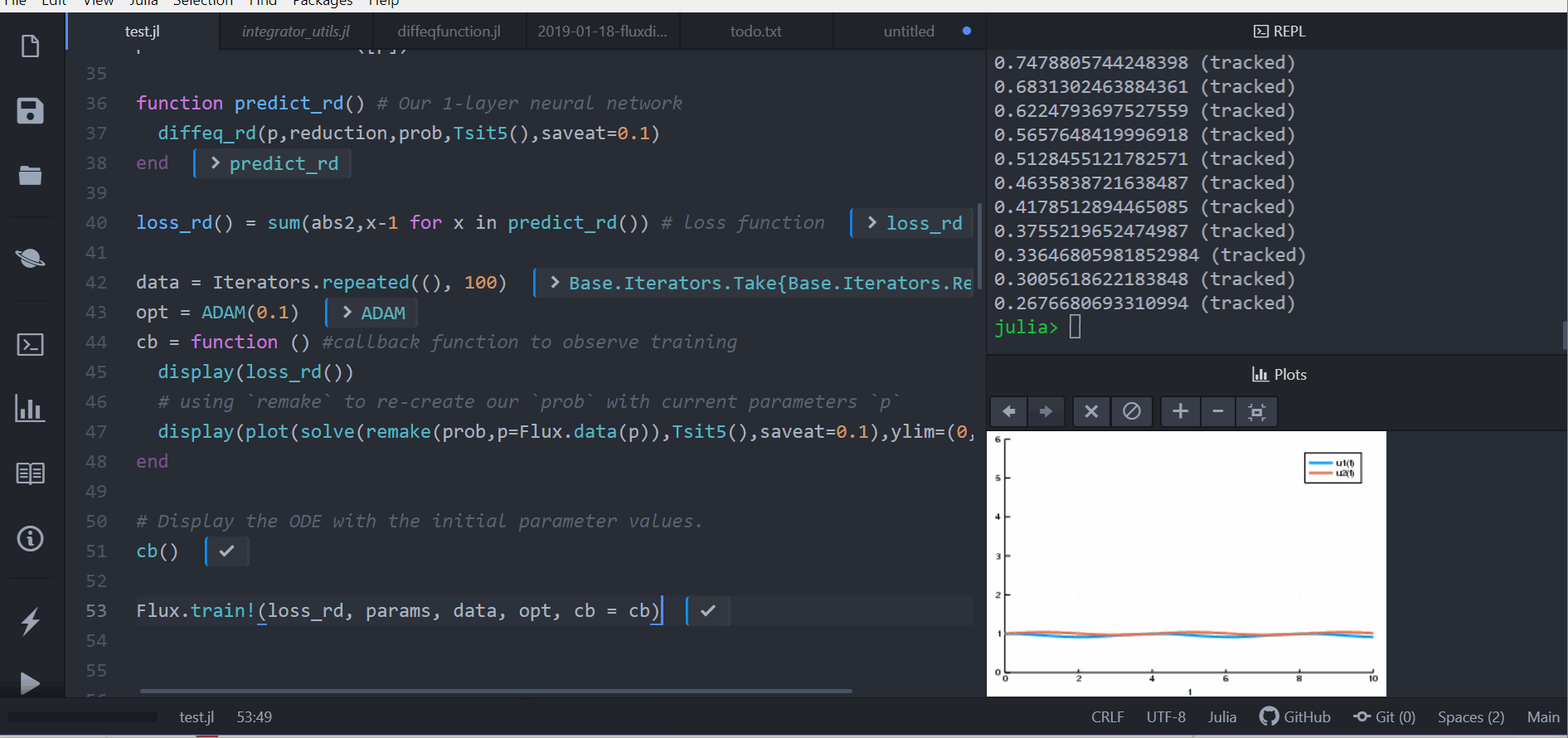
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())

Lastly, we train the neural network using Flux to arrive at parameters which optimize for our goal:

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_adjoint())
  # using `remake` to re-create our `prob` with current parameters `p`
  display(plot(solve(remake(prob,p=Flux.data(p)),Tsit5(),saveat=0.0:0.1:10.0),ylim=(0,6)))
end

# Display the ODE with the initial parameter values.
cb()

Flux.train!(loss_adjoint, params, data, opt, cb = cb)

Note that by using anonymous functions, this diffeq_adjoint can be used as a layer in a neural network Chain, for example like

m = Chain(
  Conv((2,2), 1=>16, relu),
  x -> maxpool(x, (2,2)),
  Conv((2,2), 16=>8, relu),
  x -> maxpool(x, (2,2)),
  x -> reshape(x, :, size(x, 4)),
  # takes in the ODE parameters from the previous layer
  p -> diffeq_adjoint(p,prob,Tsit5(),saveat=0.1),
  Dense(288, 10), softmax) |> gpu

m = Chain(
  Dense(28^2, 32, relu),
  # takes in the initial condition from the previous layer
  x -> diffeq_rd(p,prob,Tsit5(),saveat=0.1,u0=x)),
  Dense(32, 10),
  softmax)

Similarly, diffeq_adjoint, a O(1) memory adjoint implementation, can be replaced with diffeq_rd for reverse-mode automatic differentiation or diffeq_fd for forward-mode automatic differentiation. diffeq_fd will be fastest with small numbers of parameters, while diffeq_adjoint will be the fastest when there are large numbers of parameters (like with a neural ODE). See the layer API documentation for details.

Using Other Differential Equations

Other differential equation problem types from DifferentialEquations.jl are supported. For example, we can build a layer with a delay differential equation like:

function delay_lotka_volterra(du,u,h,p,t)
  x, y = u
  α, β, δ, γ = p
  du[1] = dx = (α - β*y)*h(p,t-0.1)[1]
  du[2] = dy = (δ*x - γ)*y
end
h(p,t) = ones(eltype(p),2)
prob = DDEProblem(delay_lotka_volterra,[1.0,1.0],h,(0.0,10.0),constant_lags=[0.1])

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_rd_dde()
  Array(diffeq_rd(p,prob,MethodOfSteps(Tsit5()),saveat=0.1))
end
loss_rd_dde() = sum(abs2,x-1 for x in predict_rd_dde())
loss_rd_dde()

Notice that we used mutating reverse-mode to handle a small delay differential equation, a strategy that can be good for small equations (see the performance discussion for more details on other forms).

Or we can use a stochastic differential equation. Here we demonstrate diffeq_fd for forward-mode automatic differentiation of a small differential equation:

function lotka_volterra_noise(du,u,p,t)
  du[1] = 0.1u[1]
  du[2] = 0.1u[2]
end
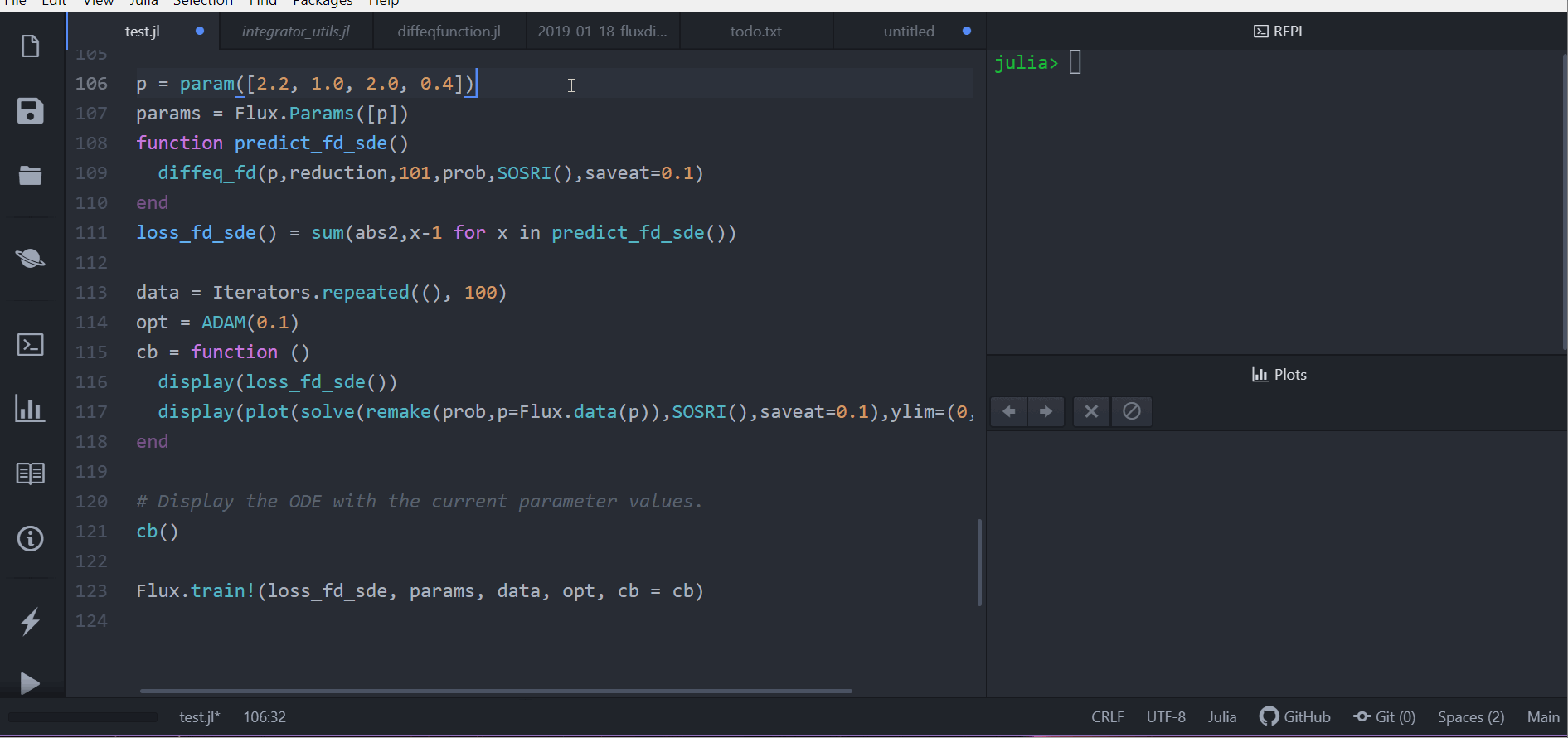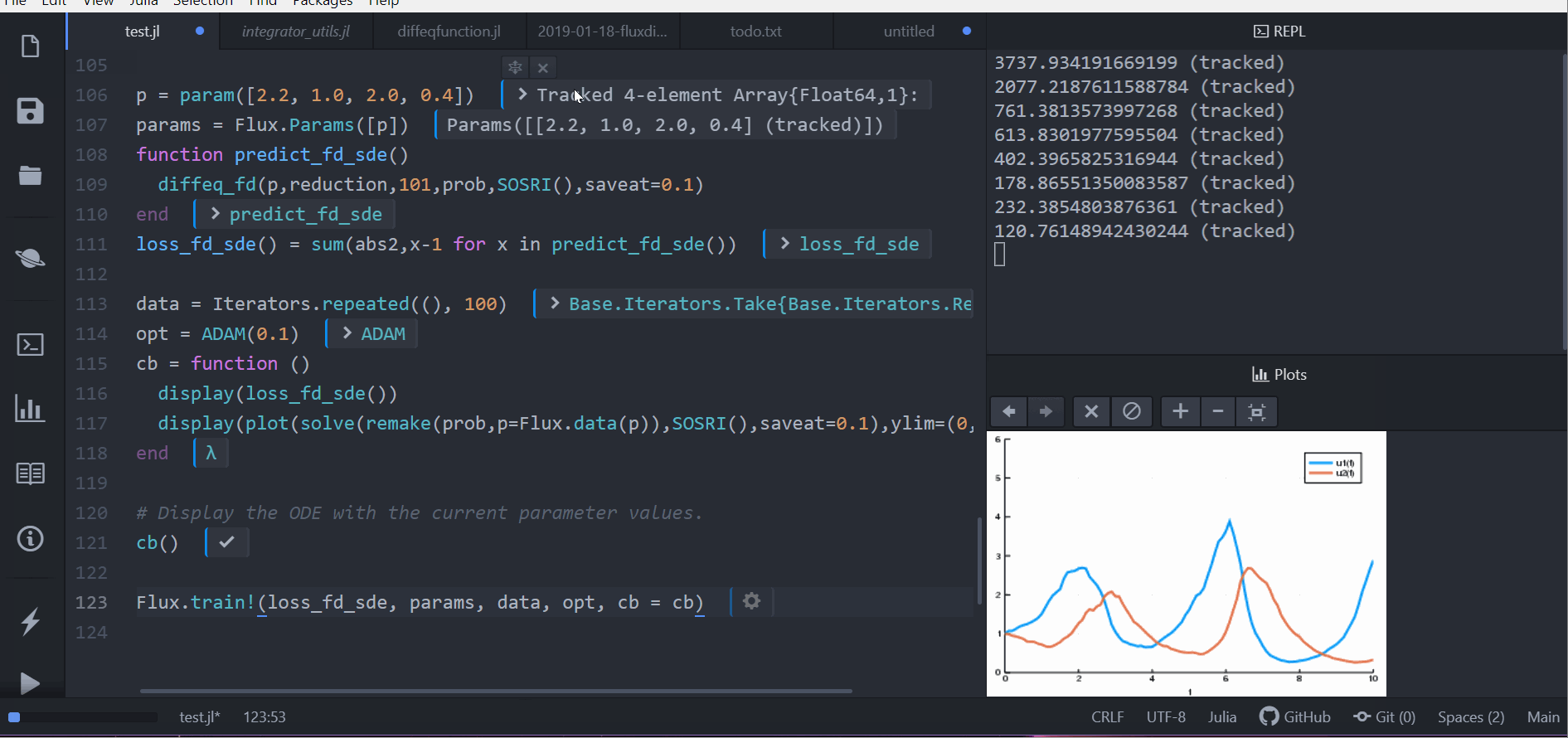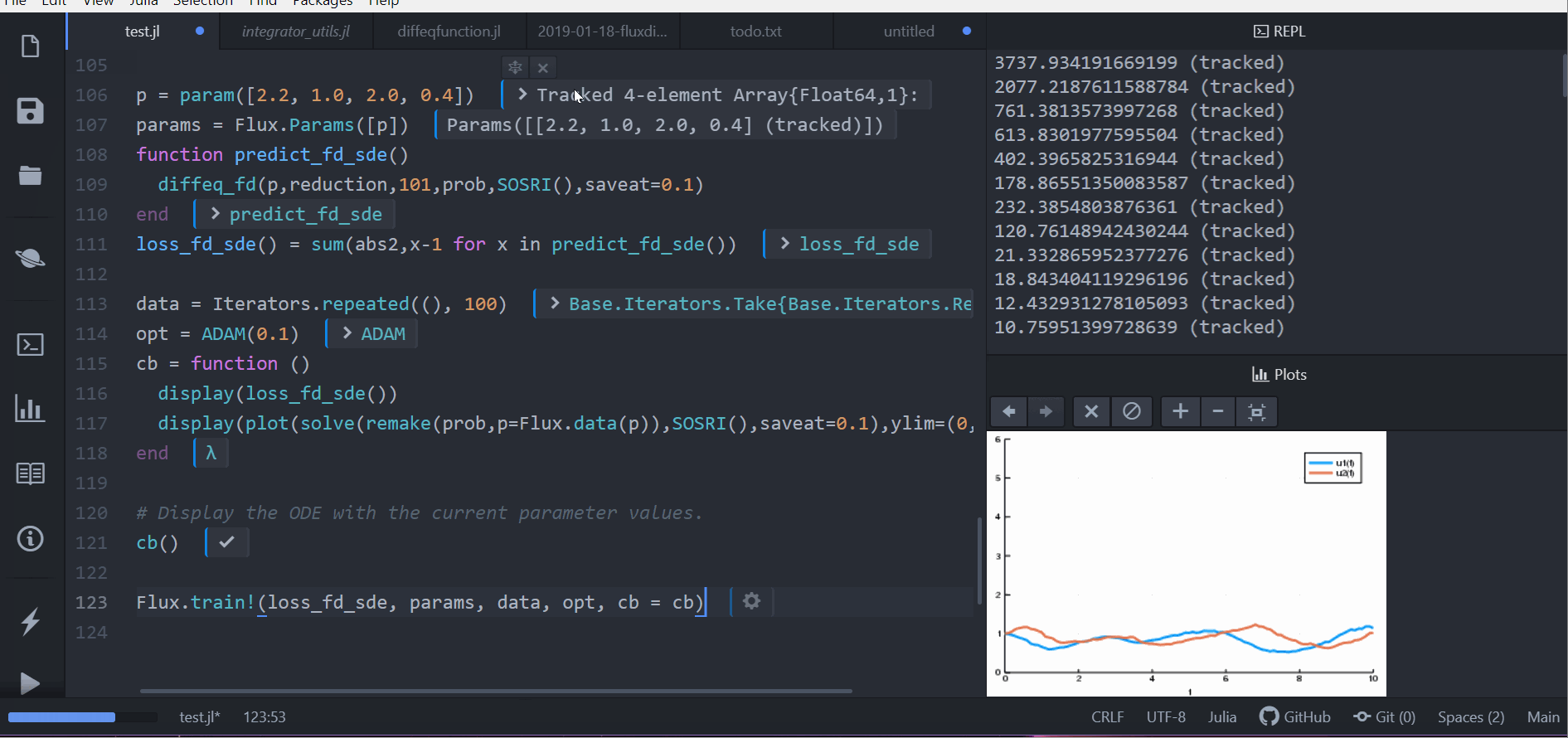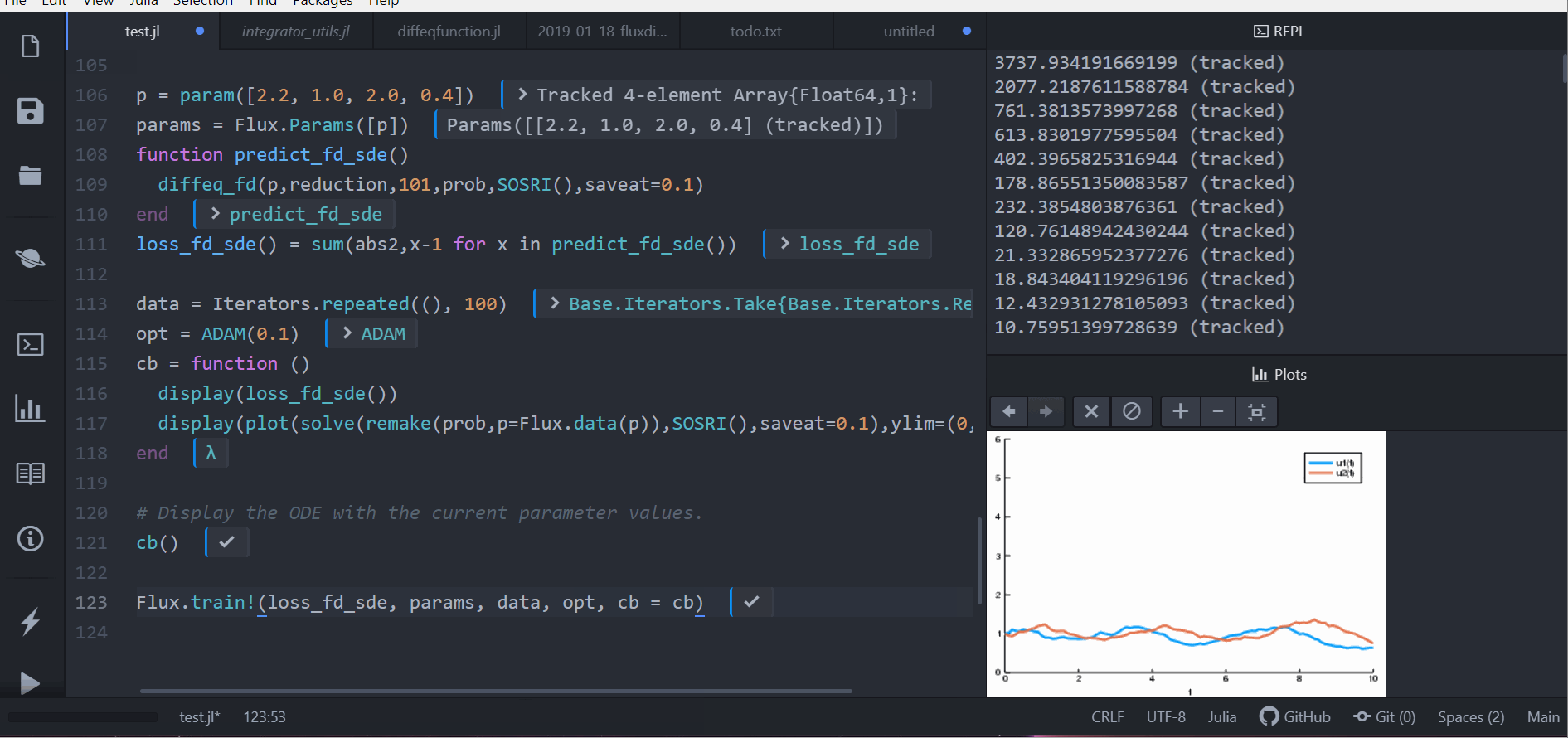
prob = SDEProblem(lotka_volterra,lotka_volterra_noise,[1.0,1.0],(0.0,10.0))

p = param([2.2, 1.0, 2.0, 0.4])
params = Flux.Params([p])
function predict_fd_sde()
  diffeq_fd(p,Array,202,prob,SOSRI(),saveat=0.1)
end
loss_fd_sde() = sum(abs2,x-1 for x in predict_fd_sde())
loss_fd_sde()

data = Iterators.repeated((), 100)
opt = ADAM(0.1)
cb = function ()
  display(loss_fd_sde())
  display(plot(solve(remake(prob,p=Flux.data(p)),SOSRI(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_fd_sde, params, data, opt, cb = cb)

Neural Ordinary Differential Equations

We can use DiffEqFlux.jl to define, solve, and train neural ordinary differential equations. A neural ODE is an ODE where a neural network defines its derivative function. Thus for example, with the multilayer perceptron neural network Chain(Dense(2,50,tanh),Dense(50,2)), the best way to define a neural ODE by hand would be to use non-mutating adjoints, which looks like:

p = DiffEqFlux.destructure(model)
dudt_(u::TrackedArray,p,t) = DiffEqFlux.restructure(model,p)(u)
dudt_(u::AbstractArray,p,t) = Flux.data(DiffEqFlux.restructure(model,p)(u))
prob = ODEProblem(dudt_,x,tspan,p)
my_neural_ode_prob = diffeq_adjoint(p,prob,args...;u0=x,kwargs...)

(DiffEqFlux.restructure and DiffEqFlux.destructure are helper functions which transform the neural network to use parameters p)

A convenience function which handles all of the details is neural_ode. To use neural_ode, you give it the initial condition, the internal neural network model to use, the timespan to solve on, and any ODE solver arguments. For example, this neural ODE would be defined as:

tspan = (0.0f0,25.0f0)
x -> neural_ode(model,x,tspan,Tsit5(),saveat=0.1)

where here we made it a layer that takes in the initial condition and spits out an array for the time series saved at every 0.1 time steps.

Training a Neural Ordinary Differential Equation

Let's get a time series array from the Lotka-Volterra equation as data:

u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.5f0)

function trueODEfunc(du,u,p,t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
prob = ODEProblem(trueODEfunc,u0,tspan)
ode_data = Array(solve(prob,Tsit5(),saveat=t))

Now let's define a neural network with a neural_ode layer. First we define the layer:

dudt = Chain(x -> x.^3,
             Dense(2,50,tanh),
             Dense(50,2))
n_ode(x) = neural_ode(dudt,x,tspan,Tsit5(),saveat=t,reltol=1e-7,abstol=1e-9)

Here we used the x -> x.^3 assumption in the model. By incorporating structure into our equations, we can reduce the required size and training time for the neural network, but a good guess needs to be known!

From here we build a loss function around it. We will use the L2 loss of the network's output against the time series data:

function predict_n_ode()
  n_ode(u0)
end
loss_n_ode() = sum(abs2,ode_data .- predict_n_ode())

and then train the neural network to learn the ODE:

data = Iterators.repeated((), 1000)
opt = ADAM(0.1)
cb = function () #callback function to observe training
  display(loss_n_ode())
  # plot current prediction against data
  cur_pred = Flux.data(predict_n_ode())
  pl = scatter(t,ode_data[1,:],label="data")
  scatter!(pl,t,cur_pred[1,:],label="prediction")
  display(plot(pl))
end

# Display the ODE with the initial parameter values.
cb()

ps = Flux.params(dudt)
Flux.train!(loss_n_ode, ps, data, opt, cb = cb)

Use with GPUs

Note that the differential equation solvers will run on the GPU if the initial condition is a GPU array. Thus for example, we can define a neural ODE by hand that runs on the GPU:

u0 = Float32[2.; 0.] |> gpu
dudt = Chain(Dense(2,50,tanh),Dense(50,2)) |> gpu

p = DiffEqFlux.destructure(model)
dudt_(u::TrackedArray,p,t) = DiffEqFlux.restructure(model,p)(u)
dudt_(u::AbstractArray,p,t) = Flux.data(DiffEqFlux.restructure(model,p)(u))
prob = ODEProblem(ODEfunc, u0,tspan)

# Runs on a GPU
sol = solve(prob,Tsit5(),saveat=0.1)

and the diffeq layer functions can be used similarly. Or we can directly use the neural ODE layer function, like:

x -> neural_ode(gpu(dudt),gpu(x),tspan,Tsit5(),saveat=0.1)

Mixed Neural DEs

You can also mix a known differential equation and a neural differential equation, so that the parameters and the neural network are estimated simultaniously. Here's an example of doing this with both reverse-mode autodifferentiation and with adjoints:

using DiffEqFlux, Flux, OrdinaryDiffEq

## --- Reverse-mode AD ---

tspan = (0.0f0,25.0f0)
u0 = Tracker.param(Float32[0.8; 0.8])

ann = Chain(Dense(2,10,tanh), Dense(10,1))
p = param(Float32[-2.0,1.1])

function dudt_(u::TrackedArray,p,t)
    x, y = u
    Flux.Tracker.collect(
        [ann(u)[1],
        p[1]*y + p[2]*x*y])
end
function dudt_(u::AbstractArray,p,t)
    x, y = u
    [Flux.data(ann(u)[1]),
    p[1]*y + p[2]*x*y]
end

prob = ODEProblem(dudt_,u0,tspan,p)
diffeq_rd(p,prob,Tsit5())

function predict_rd()
  Flux.Tracker.collect(diffeq_rd(p,prob,Tsit5(),u0=u0))
end
loss_rd() = sum(abs2,x-1 for x in predict_rd())
loss_rd()

data = Iterators.repeated((), 10)
opt = ADAM(0.1)
cb = function ()
  display(loss_rd())
  #display(plot(solve(remake(prob,u0=Flux.data(u0),p=Flux.data(p)),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_rd, params(ann,p,u0), data, opt, cb = cb)


## --- Partial Neural Adjoint ---

u0 = param(Float32[0.8; 0.8])
tspan = (0.0f0,25.0f0)

ann = Chain(Dense(2,10,tanh), Dense(10,1))

p1 = Flux.data(DiffEqFlux.destructure(ann))
p2 = Float32[-2.0,1.1]
p3 = param([p1;p2])
ps = Flux.params(p3,u0)

function dudt_(du,u,p,t)
    x, y = u
    du[1] = DiffEqFlux.restructure(ann,p[1:41])(u)[1]
    du[2] = p[end-1]*y + p[end]*x
end
prob = ODEProblem(dudt_,u0,tspan,p3)
diffeq_adjoint(p3,prob,Tsit5(),u0=u0,abstol=1e-8,reltol=1e-6)

function predict_adjoint()
  diffeq_adjoint(p3,prob,Tsit5(),u0=u0,saveat=0.0:0.1:25.0)
end
loss_adjoint() = sum(abs2,x-1 for x in predict_adjoint())
loss_adjoint()

data = Iterators.repeated((), 10)
opt = ADAM(0.1)
cb = function ()
  display(loss_adjoint())
  #display(plot(solve(remake(prob,p=Flux.data(p3),u0=Flux.data(u0)),Tsit5(),saveat=0.1),ylim=(0,6)))
end

# Display the ODE with the current parameter values.
cb()

Flux.train!(loss_adjoint, ps, data, opt, cb = cb)

Neural Differential Equations for Non-ODEs: Neural SDEs, Neural DDEs, etc.

With neural stochastic differential equations, there is once again a helper form neural_dmsde which can be used for the multiplicative noise case (consult the layers API documentation, or this full example using the layer function).

However, since there are far too many possible combinations for the API to support, in many cases you will want to performantly define neural differential equations for non-ODE systems from scratch. For these systems, it is generally best to use diffeq_rd with non-mutating (out-of-place) forms. For example, the following defines a neural SDE with neural networks for both the drift and diffusion terms:

dudt_(u,p,t) = model(u)
g(u,p,t) = model2(u)
prob = SDEProblem(dudt_,g,param(x),tspan,nothing)

where model and model2 are different neural networks. The same can apply to a neural delay differential equation. Its out-of-place formulation is f(u,h,p,t). Thus for example, if we want to define a neural delay differential equation which uses the history value at p.tau in the past, we can define:

dudt_(u,h,p,t) = model([u;h(t-p.tau)])
prob = DDEProblem(dudt_,u0,h,tspan,nothing)

Neural SDE Example

First let's build training data from the same example as the neural ODE:

using Flux, DiffEqFlux, StochasticDiffEq, Plots, DiffEqBase.EnsembleAnalysis

u0 = Float32[2.; 0.]
datasize = 30
tspan = (0.0f0,1.0f0)

function trueODEfunc(du,u,p,t)
    true_A = [-0.1 2.0; -2.0 -0.1]
    du .= ((u.^3)'true_A)'
end
t = range(tspan[1],tspan[2],length=datasize)
mp = Float32[0.2,0.2]
function true_noise_func(du,u,p,t)
    du .= mp.*u
end
prob = SDEProblem(trueODEfunc,true_noise_func,u0,tspan)

For our dataset we will use DifferentialEquations.jl's parallel ensemble interface to generate data from the average of 100 runs of the SDE:

# Take a typical sample from the mean
ensemble_prob = EnsembleProblem(prob)
ensemble_sol = solve(ensemble_prob,SOSRI(),trajectories = 100)
ensemble_sum = EnsembleSummary(ensemble_sol)
sde_data = Array(timeseries_point_mean(ensemble_sol,t))

Now we build a neural SDE. For simplicity we will use the neural_dmsde multiplicative noise neural SDE layer function:

dudt = Chain(x -> x.^3,
             Dense(2,50,tanh),
             Dense(50,2))
ps = Flux.params(dudt)
n_sde = x->neural_dmsde(dudt,x,mp,tspan,SOSRI(),saveat=t,reltol=1e-1,abstol=1e-1)

Let's see what that looks like:

pred = n_sde(u0) # Get the prediction using the correct initial condition

dudt_(u,p,t) = Flux.data(dudt(u))
g(u,p,t) = mp.*u
nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)

ensemble_nprob = EnsembleProblem(nprob)
ensemble_nsol = solve(ensemble_nprob,SOSRI(),trajectories = 100)
ensemble_nsum = EnsembleSummary(ensemble_nsol)
p1 = plot(ensemble_nsum, title = "Neural SDE: Before Training")
scatter!(p1,t,sde_data',lw=3)

scatter(t,sde_data[1,:],label="data")
scatter!(t,Flux.data(pred[1,:]),label="prediction")

Now just as with the neural ODE we define a loss function:

function predict_n_sde()
  n_sde(u0)
end
loss_n_sde1() = sum(abs2,sde_data .- predict_n_sde())
loss_n_sde10() = sum([sum(abs2,sde_data .- predict_n_sde()) for i in 1:10])
Flux.back!(loss_n_sde1())

data = Iterators.repeated((), 10)
opt = ADAM(0.025)
cb = function () #callback function to observe training
  sample = predict_n_sde()
  # loss against current data
  display(sum(abs2,sde_data .- sample))
  # plot current prediction against data
  cur_pred = Flux.data(sample)
  pl = scatter(t,sde_data[1,:],label="data")
  scatter!(pl,t,cur_pred[1,:],label="prediction")
  display(plot(pl))
end

# Display the SDE with the initial parameter values.
cb()

Here we made two loss functions: one which uses single runs of the SDE and another which uses multiple runs. This is beceause an SDE is stochastic, so trying to fit the mean to high precision may require a taking the mean of a few trajectories (the more trajectories the more precise the calculation is). Thus to fit this, we first get in the general area through single SDE trajectory backprops, and then hone in with the mean:

Flux.train!(loss_n_sde1 , ps, Iterators.repeated((), 100), opt, cb = cb)
Flux.train!(loss_n_sde10, ps, Iterators.repeated((), 20), opt, cb = cb)

And now we plot the solution to an ensemble of the trained neural SDE:

dudt_(u,p,t) = Flux.data(dudt(u))
g(u,p,t) = mp.*u
nprob = SDEProblem(dudt_,g,u0,(0.0f0,1.2f0),nothing)

ensemble_nprob = EnsembleProblem(nprob)
ensemble_nsol = solve(ensemble_nprob,SOSRI(),trajectories = 100)
ensemble_nsum = EnsembleSummary(ensemble_nsol)
p2 = plot(ensemble_nsum, title = "Neural SDE: After Training", xlabel="Time")
scatter!(p2,t,sde_data',lw=3,label=["x" "y" "z" "y"])

plot(p1,p2,layout=(2,1))

(note: for simplicity we have used a constant mp vector, though once can param and train this value as well.)

Try this with GPUs as well!

Neural Jump Diffusions (Neural Jump SDE) and Neural Partial Differential Equations (Neural PDEs)

For the sake of not having a never-ending documentation of every single combination of CPU/GPU with every layer and every neural differential equation, we will end here. But you may want to consult this blog post which showcases defining neural jump diffusions and neural partial differential equations.

A Note About Performance

DiffEqFlux.jl implements all interactions of automatic differentiation systems to satisfy completeness, but that does not mean that every combination is a good combination.

Performance tl;dr

Use diffeq_adjoint with an out-of-place non-mutating function f(u,p,t) on ODEs without events.
Use diffeq_rd with an out-of-place non-mutating function (f(u,p,t) on ODEs/SDEs, f(du,u,p,t) for DAEs, f(u,h,p,t) for DDEs, and consult the docs for other equations) for non-ODE neural differential equations or ODEs with events
If the neural network is a sufficiently small (or non-existant) part of the differential equation, consider diffeq_fd with the mutating form (f(du,u,p,t)).
Always use GPUs if the majority of the time is in larger kernels (matrix multiplication, PDE convolutions, etc.)

Extended Performance Discussion

The major options to keep in mind are:

in-place vs out-of-place: for ODEs this amounts to f(du,u,p,t) mutating du vs du = f(u,p,t). In almost all scientific computing scenarios with floating point numbers, f(du,u,p,t) is highly preferred. This extends to dual numbers and thus forward difference (diffeq_fd). However, reverse-mode automatic differentiation as implemented by Flux.jl's Tracker.jl does not allow for mutation on its TrackedArray type, meaning that mutation is supported by Array{TrackedReal}. This fallback is exceedingly slow due to the large trace that is created, and thus out-of-place (f(u,p,t) for ODEs) is preferred in this case.
For adjoints, this fact is complicated due to the choices in the SensitivityAlg. See the adjoint SensitivityAlg options for more details. When autojacvec=true, a backpropogation is performed by Tracker in the intermediate steps, meaning the rule about mutation applies. However, the majority of the computation is not hte v^T*J computation of the backpropogation, so it is not always obvious to determine the best option given that mutation is slow for backprop but is much faster for large ODEs with many scalar operations. But the latter portion of that statement is the determiner: if there are sufficiently large operations which are dominating the runtime, then the backpropogation can be made trivial by using mutation, and thus f(u,p,t) is more efficient. One example which falls into this case is the neural ODE which has large matrix multiply operations. However, if the neural network is a small portion of the equation and there is heavy reliance on directly specified nonlinear forms in the differential equation, f(du,u,p,t) with the option sense=SensitivityAlg(autojacvec=false) may be preferred.
diffeq_adjoint currently only applies to ODEs, though continued development will handle other equations in the future.
diffeq_adjoint has O(1) memory with the default backsolve. However, it is known that this is unstable on many equations with high enough stiffness (this is a fundamental fact of the numerics, see the blog post for details and an example. Likewise, this instability is not often seen when training a neural ODE against real data. Thus it is recommended to try with the default options first, and then set backsolve=false if unstable gradients are found. When backsolve=false is set, this will trigger the SensitivityAlg to use checkpointed adjoints, which are more stable but take more computation.
When the equation has small enough parameters, or they are not confined to large operations, diffeq_fd will be the fastest. However, as it is well-known, forward-mode AD does not scale well for calculating the gradient with respect to large numbers of parameters, and thus it will not scale well in cases like the neural ODE.

API Documentation

DiffEq Layer Functions

diffeq_rd(p,prob, args...;u0 = prob.u0, kwargs...) uses Flux.jl's reverse-mode AD through the differential equation solver with parameters p and initial condition u0. The rest of the arguments are passed to the differential equation solver. The return is the DESolution. Note: if you use this function, it is much better to use the allocating out of place form (f(u,p,t) for ODEs) than the in place form (f(du,u,p,t) for ODEs)!
diffeq_fd(p,reduction,n,prob,args...;u0 = prob.u0, kwargs...) uses ForwardDiff.jl's forward-mode AD through the differential equation solver with parameters p and initial condition u0. n is the output size where the return value is reduction(sol). The rest of the arguments are passed to the differential equation solver.
diffeq_adjoint(p,prob,args...;u0 = prob.u0, kwargs...) uses adjoint sensitivity analysis to "backprop the ODE solver" via DiffEqSensitivity.jl. The return is the time series of the solution as an array solved with parameters p and initial condition u0. The rest of the arguments are passed to the differential equation solver or handled by the adjoint sensitivity algorithm (for more details on sensitivity arguments, see the diffeq documentation). It is possible to specify separate callbacks for the forward and adjoint solutions. Passing a value for the keyword callback will attach a callback to the forward solve, whereas passing a value for the keyword callback_adj will attach a callback to the adjoint solve. This might be useful for e.g. observing function values and gradients during training.

Neural DE Layer Functions

neural_ode(model,x,tspan,args...;kwargs...) defines a neural ODE layer where model is a Flux.jl model, x is the initial condition, tspan is the time span to integrate, and the rest of the arguments are passed to the ODE solver. The parameters should be implicit in the model. Same args and kwargs are passed to the forward and adjoint solvers, as specified in diffeq_adjoint, with the exception of callback_adj, which is a separate callback passed only to the adjoint sensitivity algorithm.
neural_ode_rd(model,x,tspan,args...;kwargs...) defines a neural ODE layer, just like neural_ode, but uses Flux.jl's reverse-mode automatic differentiation to compute the gradients.
neural_dmsde(model,x,mp,tspan,args...;kwargs) defines a neural multiplicative SDE layer where model is a Flux.jl model, x is the initial condition, tspan is the time span to integrate, and the rest of the arguments are passed to the SDE solver. The noise is assumed to be diagonal multiplicative, i.e. the Wiener term is mp.*u.*dW for some array of noise constants mp.

Benchmarks

A raw ODE solver benchmark showcases a 50,000x performance advantage over torchdiffeq on small ODEs.

brucejunlee/DiffEqFlux.jl