Modifications to GPU Hardware to benefit Signed Distance Fields
The Signed Distance Field (SDF) is a fundamental primitive used in computer graphics, which has the nice property that it encodes a surface in 3D space, which regardless of topological complexity can be filtered efficiently for automatic level-of-detail by massively parallel hardware, much as a texture map can.
This makes SDF amenable to implementation in GPU hardware, though to date no hardware has been designed specifically to accelerate SDF. Rather, whatever hardware was developed for triangle rasterization has been repurposed for SDF by end users.
In this article we explore possible changes to GPU hardware specifically for the purpose of accelerating SDF.
Texture Format
For a 3D SDF texture we can store a much smaller "meta texture" in which each block of 8x8x8 texels is encoded as 16 bits: 8 bits of "minimum distance in block" and 8 bits of "maximum distance in block". This is 0.004 bits per texel, and is sufficient information to traverse an SDF much of the time. While this is reminiscent of the endpoints of a traditionally block-compressed texture, it would be stored in separate cachelines from any per-texel information, to avoid wasting memory bandwidth on such information when it isn't relevant. Many SDF fetches don't need the precise value of an individual texel, but rather wish to compare it to a known range of values. As with PCF filtering of shadow maps, the comparison can be a part of the fetch instruction itself.
When it is necessary to read per-texel information, since for most texels the value can be predicted from adjacent texels (most texels are "exactly one unit" further away from the surface than their neighbors) a simple predictive decoder in hardware is likely efficient. An 8x8x8 block that holds a flat piece of surface will likely need to encode information for only 25% of the texels, and the rest can be predicted trivially.
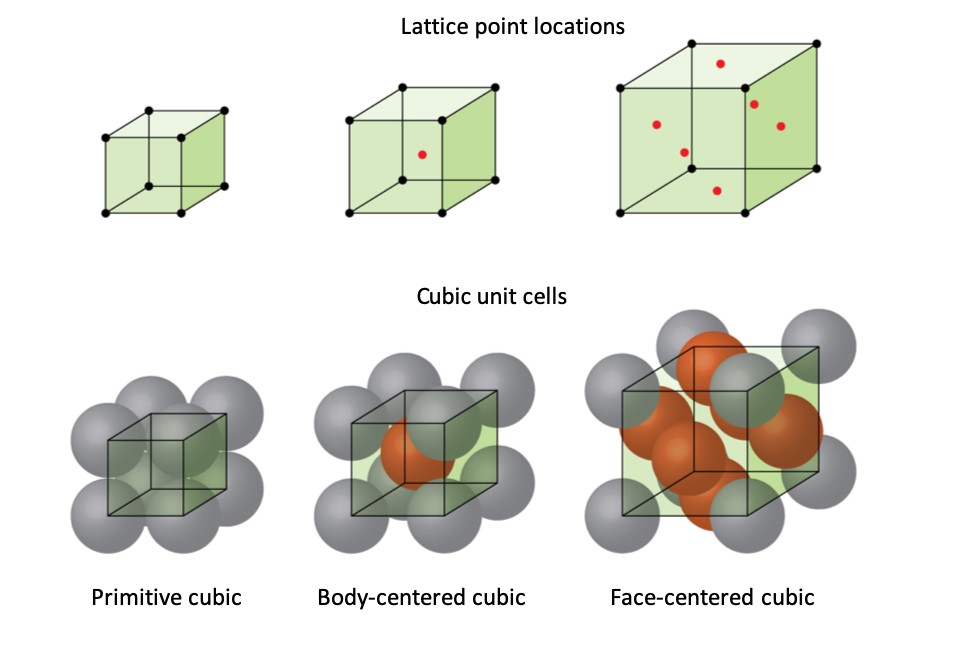
Face Centered Cubic Volume Textures
The Nintendo 64 game console did not tap the 4 nearest samples in a 2D grid to bilinearly filter a 2D texture, as contemporary hardware does. Rather, it tapped the 3 nearest samples, and linearly blended among them. For a given dimension N, a bilinear filter requires pow(2,N) taps, and a linear filter requires N+1 taps. In ten dimensions bilinear would require 1024 taps, and linear 11. So, any hardware that aims to sample a high dimensional function would be under great pressure to use linear filtering, rather than bilinear filtering.
An N64 texture can be conceptualized as being made of triangular texels, rather than the square texels of contemporary hardware.
In 3D such a texture would be made of rhombic dodecahedral texels rather than cubic texels, in a Face Centered Cubic lattice (see above image) rather than the Primitive Cubic lattice of contemporary hardware.
An SDF encoded as a 3D texture would require 4 taps with a linear filter, rather than 8 taps with a bilinear filter. The pipeline to blend 1/2 as many taps would require 1 less bit of internal precision, and would process 1/2 as much data at any instant. This may present opportunities to increase the degree of parallelism by a factor of 2.