Optimal Transport Tools (OTT)

What is OTT-JAX?

A JAX powered library to compute optimal transport at scale and on accelerators, OTT-JAX includes the fastest implementation of the Sinkhorn algorithm you will find around. We have implemented all tweaks (scheduling, acceleration, initializations) and extensions (low-rank), that can be used directly, or within more advanced problems (Gromov-Wasserstein, barycenters). Some of JAX features, including JIT, auto-vectorization and implicit differentiation work towards the goal of having end-to-end differentiable outputs. OTT-JAX is developed by a team of researchers from Apple, Google, Meta and many academic contributors, including TU München, Oxford, ENSAE/IP Paris and the Hebrew University.

Installation

Install OTT-JAX from PyPI as:

pip install ott-jax

or with conda via conda-forge as:

conda install -c conda-forge ott-jax

What is optimal transport?

Optimal transport can be loosely described as the branch of mathematics and optimization that studies matching problems: given two families of points, and a cost function on pairs of points, find a "good" (low cost) way to associate bijectively to every point in the first family another in the second.

Such problems appear in all areas of science, are easy to describe, yet hard to solve. Indeed, while matching optimally two sets of $n$ points using a pairwise cost can be solved with the Hungarian algorithm, solving it costs an order of $O(n^3)$ operations, and lacks flexibility, since one may want to couple families of different sizes.

Optimal transport extends all of this, through faster algorithms (in $n^2$ or even linear in $n$) along with numerous generalizations that can help it handle weighted sets of different size, partial matchings, and even more evolved so-called quadratic matching problems.

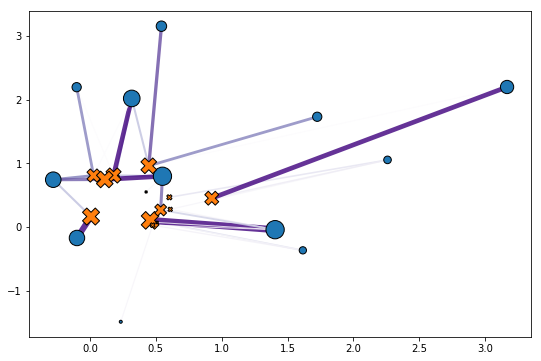
In the simple toy example below, we compute the optimal coupling matrix between two point clouds sampled randomly (2D vectors, compared with the squared Euclidean distance):

Example

import jax
import jax.numpy as jnp

from ott.geometry import pointcloud
from ott.problems.linear import linear_problem
from ott.solvers.linear import sinkhorn

# sample two point clouds and their weights.
rngs = jax.random.split(jax.random.PRNGKey(0), 4)
n, m, d = 12, 14, 2
x = jax.random.normal(rngs[0], (n,d)) + 1
y = jax.random.uniform(rngs[1], (m,d))
a = jax.random.uniform(rngs[2], (n,))
b = jax.random.uniform(rngs[3], (m,))
a, b = a / jnp.sum(a), b / jnp.sum(b)
# Computes the couplings using the Sinkhorn algorithm.
geom = pointcloud.PointCloud(x, y)
prob = linear_problem.LinearProblem(geom, a, b)

solver = sinkhorn.Sinkhorn()
out = solver(prob)

The call to solver(prob) above works out the optimal transport solution. The out object contains a transport matrix (here of size $12\times 14$) that quantifies a link strength between each point of the first point cloud, to one or more points from the second, as illustrated in the plot below. We provide more flexibility to define custom cost functions, objectives, and solvers, as detailed in the full documentation.

Citation

If you have found this work useful, please consider citing this reference: