Here is a collection of MATLAB code (compatible with Octave) that might be of some help in solving various types of computational fluid dynamics problems. Functionally the codes produce valid results; however, I am sure there is room for improvement from an efficiency standpoint. The original project description from my professor is also posted for each type of problem.
Tested with Octave 6.2.0 (arm64 Mac)
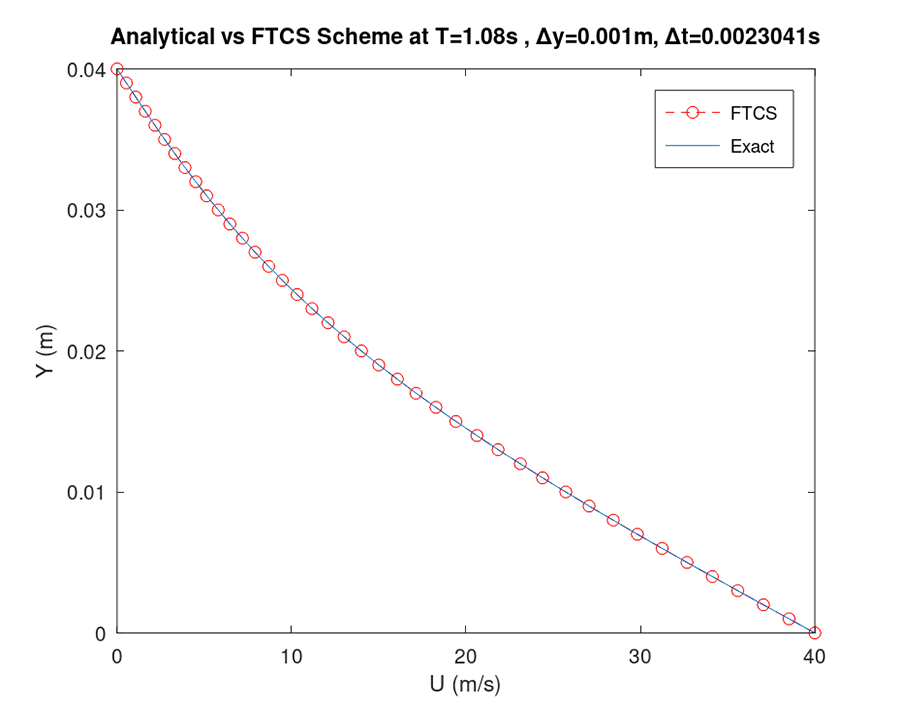
Finite difference approximation of a given couette flow between two parallel plates. The fluid has a constant kinematic viscosity and density. The upper plate is stationary and the lower one is suddenly set in motion with a constant velocity. Governing partial differential equation (PDE) is discretized using a first-order forward-time and second-order central space (FTCS) scheme.
See Description
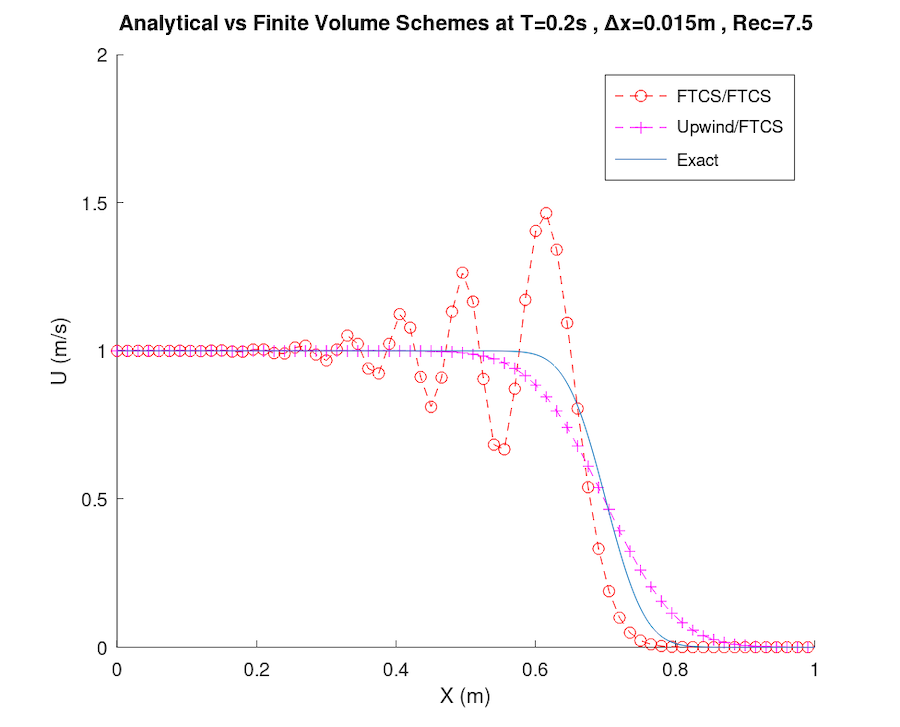
Comparison between finite difference and finite volume approximations of wave propagation inside a one-dimensional channel. Fluid velocity and diffusion coefficient are given in addition to initial conditions along the channel and boundary conditions at the inlet and outlet. Forward Time-Centered Space (FTCS) and first-order upwind are used for finite volume approximations while FTCS, first-order upwind, Lax-Wendroff and MacCormack are used for finite difference.
See Description
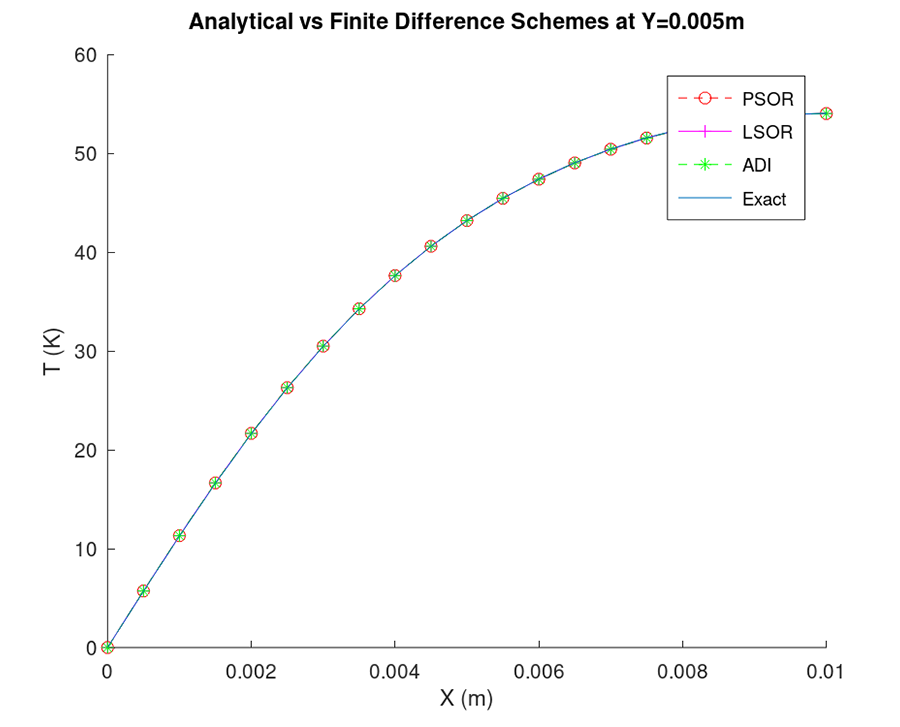
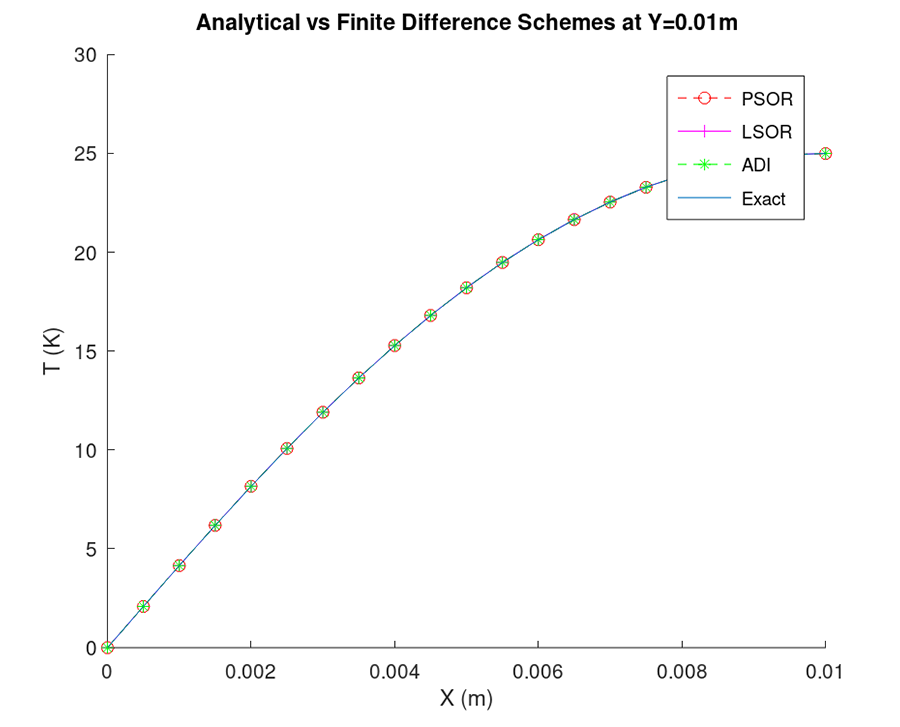
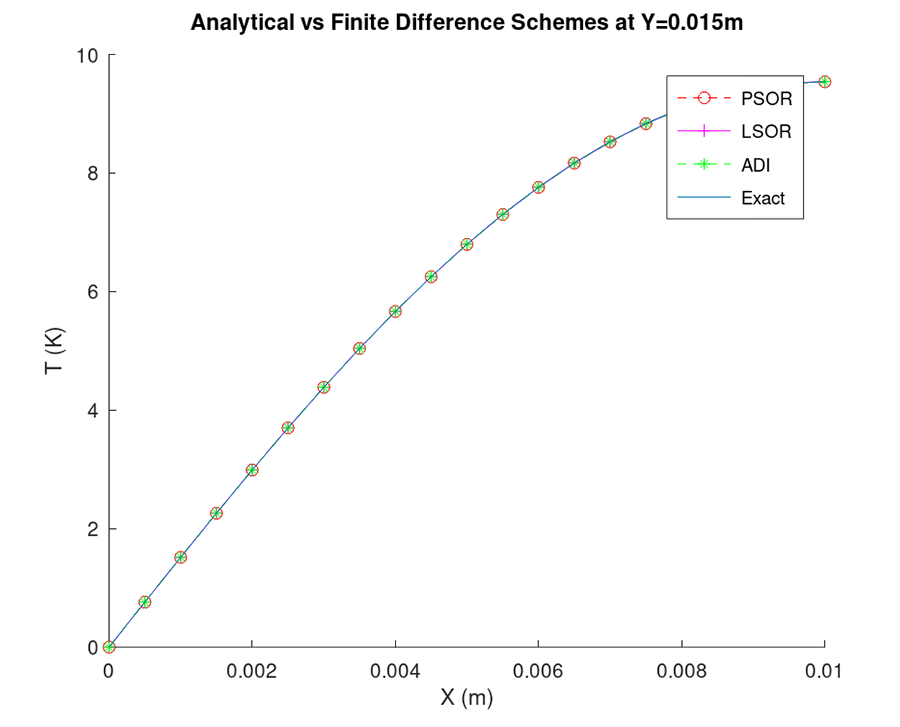
Steady-state temperature distribution of a two-dimensional rectangular plate is approximated using finite difference method. Plate dimensions and boundary conditions at the edges are given. Different types of relaxation are applied: Point Successive Over-Relaxation (PSOR), Line Successive Over-Relaxation (LSOR), and Alternative Direction Implicit (ADI).
See Description
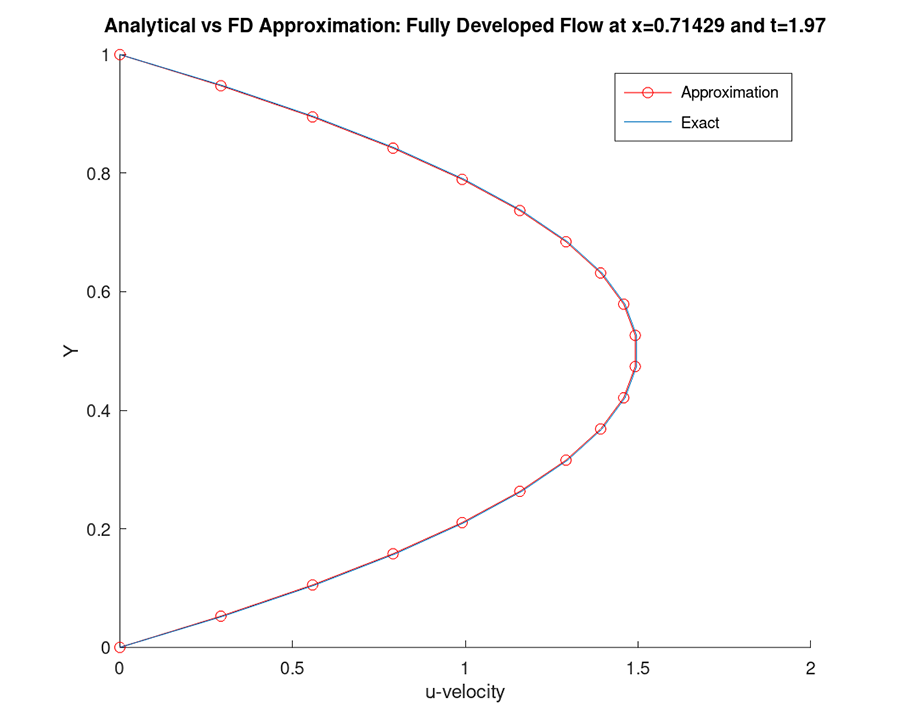
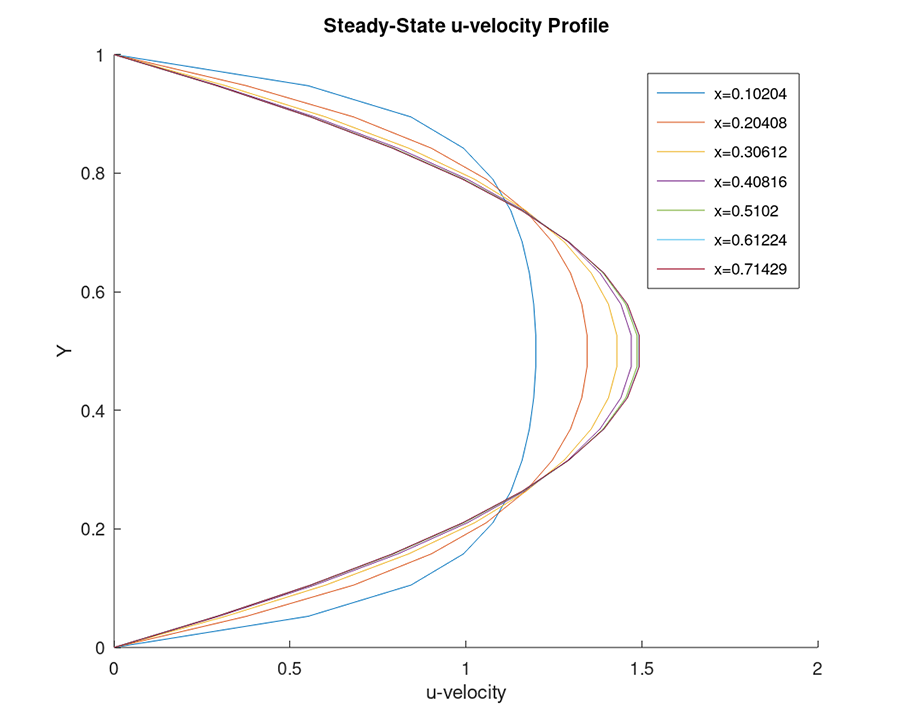
The steady-state u-velocity profile of an incompressible laminar flow within a plane channel is approximated using finite difference. The flow is governed by both vorticity and stream-function transport equations.
See Description