| title | output | vignette |
|---|---|---|
R package multipleROC |
rmarkdown::html_vignette |
%\VignetteIndexEntry{multipleROC} %\VignetteEngine{knitr::rmarkdown} %\VignetteEncoding{UTF-8}
|
R package multipleROC is for ROC analysis with models with multiple predictors. You can draw a ROC plot with ggplot2 for models with multiple predictors. You can draw several ROC curves in a plot. You can perform automatic stepwise logistic regression analysis and compare the initial and final models.
You can install multipleROC package from github.
install.packages("remotes")
remotes::install_github("cardiomoon/multipleROC")library(multipleROC)Data radial from package moonBook is a dataset containing demographic data and laboratory data of 115 patients. If you want to differentiate male and female patients with their heights(in centimeter), you can perform exploratory analysis first.
library(webr)
library(ggplot2)
library(dplyr)
library(tidyr)
theme_set(theme_bw())
data(radial,package="moonBook")
radial %>% group_by(sex) %>% numSummaryTable(height)sex | n | mean | sd | median | trimmed | mad | min | max | range | skew | kurtosis | se |
F | 56.00 | 153.61 | 6.01 | 153.00 | 153.70 | 5.93 | 140.00 | 166.00 | 26.00 | -0.07 | -0.46 | 0.80 |
M | 58.00 | 167.53 | 5.84 | 169.00 | 167.48 | 5.93 | 155.00 | 180.00 | 25.00 | -0.01 | -0.60 | 0.77 |
ggplot(data=radial)+geom_density(aes(x=height,fill=sex),alpha=0.5)
ggplot(data=radial)+geom_boxplot(aes(x=sex,y=height,fill=sex),alpha=0.5)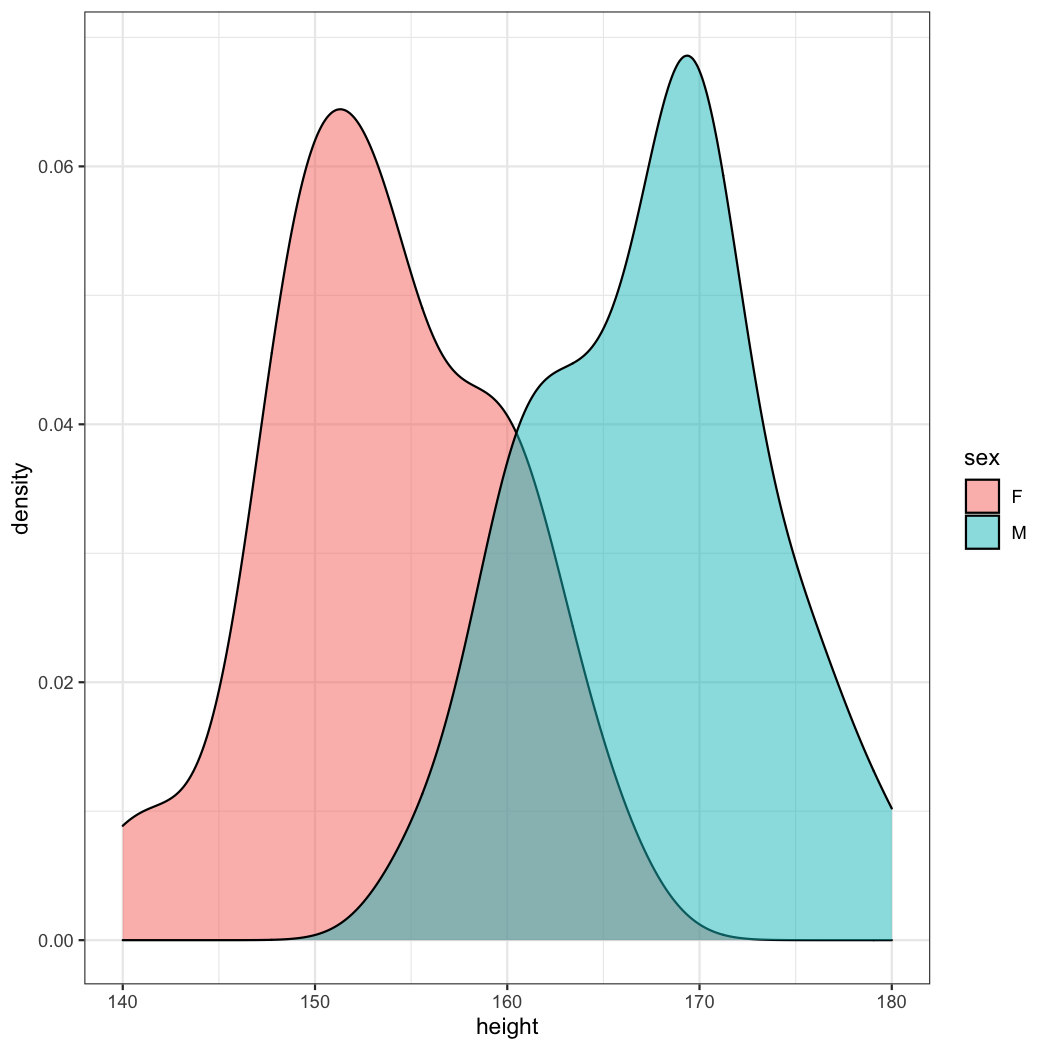 
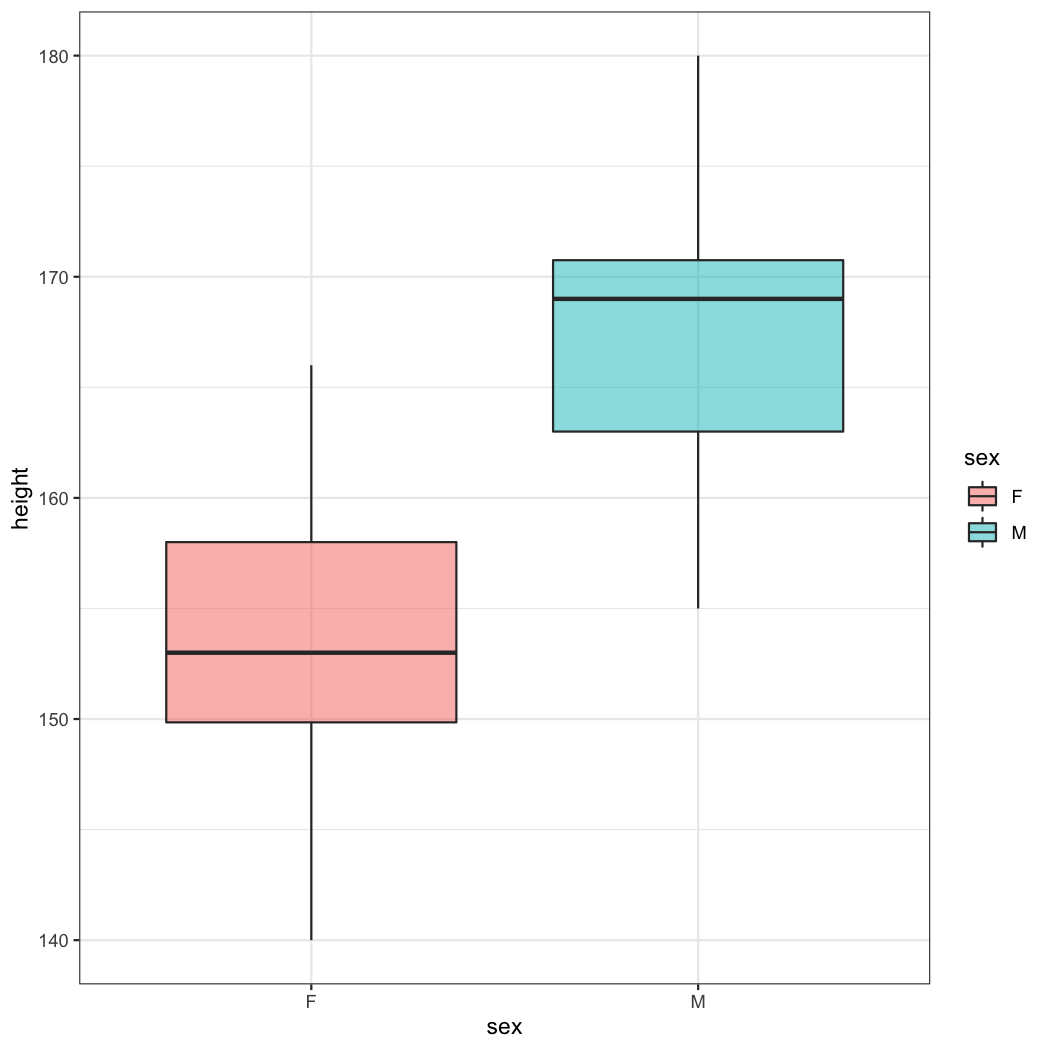As you can see, male patients are taller than female patients. But how can I determine the optimal cutoff value?
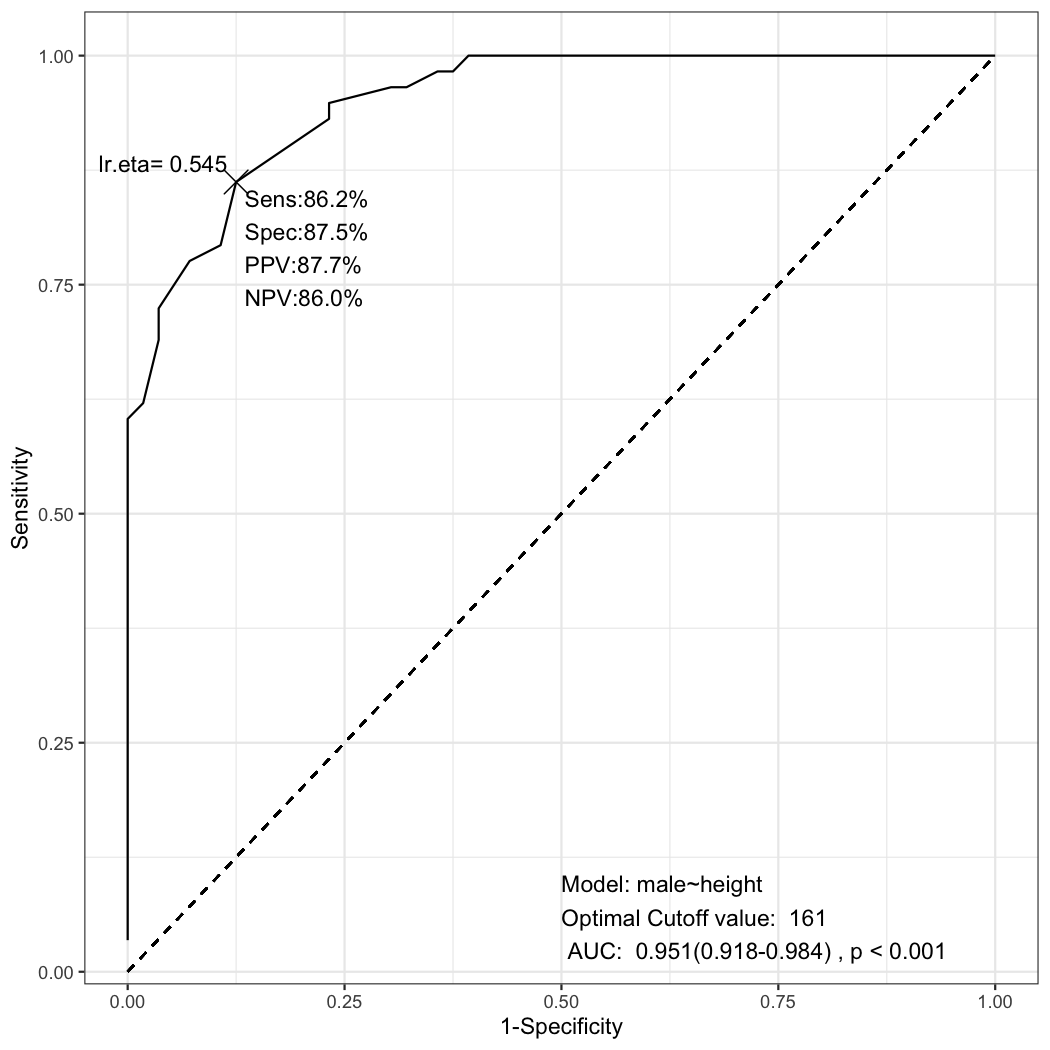
To draw a ROC curve is one of the useful method to determine the optimal cutoff value. You can perform ROC analysis using the following R command.The following R command makes an object of class multipleROC and makes a plot.
data(radial,package="moonBook")
x=multipleROC(male~height,data=radial)
You can see the ROC plot with sensitivity(Sens), specificity(Spec), positive predictive value(PPV) and negative predictive value(NPV) with the cutoff value 161. These rates comes from the following table.
table(radial$height>=161,radial$male)
0 1
FALSE 49 8
TRUE 7 50If you use the height
\begin{equation} Sensitivity=\frac{TP}{Male, Patients}=\frac{TP}{FN+TP}=\frac{50}{8+50}=86.2 % \end{equation}
Specificity measures a test’s ability to correctly generate a negative result for people who don’t have the condition that’s being tested for (also known as the “true negative” rate).
\begin{equation} Specificity=\frac{TN}{Female, Patients}=\frac{TN}{TN+FP}=\frac{49}{49+7}=87.5 % \end{equation}
Positive predictive value(PPV) is calculated as follows:
\begin{equation} PPV=\frac{TP}{Pts,with, height \geq 161cm}=\frac{TP}{TP+FP}=\frac{50}{50+7}=87.7% \end{equation}
Negative predictive value(PPV) is calculated as follows:
\begin{equation} NPV=\frac{TN}{Pts,with, height < 161cm}=\frac{TN}{TN+FN}=\frac{49}{49+8}= 85.9 % \end{equation}
You can calculate the sensitivity, specificity for all the height data of radial. The radial data are from 115 patients, but 1 patient's height is missed. But the length of unique values of radial$height is 39 due to duplication.
length(unique(radial$height))
[1] 39You can calculate all the ratio by hand. For your convenience, you can use calSens() function included in multipleROC package.
calSens=function(x,y){
newx=sort(unique(x))
completeTable=function(res){
if(nrow(res)==1){
res1=matrix(c(0,0),nrow=1)
temp=setdiff(c("TRUE","FALSE"),attr(res,"dimnames")[[1]][1])
if(temp=="FALSE") res=rbind(res1,res)
else res=rbind(res,res1)
res
}
res
}
getSens=function(cut){
res=table(x>=cut,y)
res=completeTable(res)
sens=res[2,2]/sum(res[,2])
spec=res[1,1]/sum(res[,1])
ppv=res[2,2]/sum(res[2,])
npv=res[1,1]/sum(res[1,])
data.frame(x=cut,sens=sens,spec=spec,fpr=1-spec,ppv=ppv,npv=npv,sum=sens+spec)
}
map_dfr(newx,function(cut){getSens(cut)})
}result=calSens(radial$height,radial$male)
result
x sens spec fpr ppv npv sum
1 140.0 1.00000000 0.00000000 1.00000000 0.5087719 NaN 1.000000
2 142.0 1.00000000 0.03571429 0.96428571 0.5178571 1.0000000 1.035714
3 144.0 1.00000000 0.05357143 0.94642857 0.5225225 1.0000000 1.053571
4 147.0 1.00000000 0.07142857 0.92857143 0.5272727 1.0000000 1.071429
5 147.5 1.00000000 0.08928571 0.91071429 0.5321101 1.0000000 1.089286
6 148.0 1.00000000 0.10714286 0.89285714 0.5370370 1.0000000 1.107143
7 149.0 1.00000000 0.17857143 0.82142857 0.5576923 1.0000000 1.178571
8 149.4 1.00000000 0.23214286 0.76785714 0.5742574 1.0000000 1.232143
9 150.0 1.00000000 0.25000000 0.75000000 0.5800000 1.0000000 1.250000
10 151.0 1.00000000 0.35714286 0.64285714 0.6170213 1.0000000 1.357143
11 152.0 1.00000000 0.37500000 0.62500000 0.6236559 1.0000000 1.375000
12 153.0 1.00000000 0.42857143 0.57142857 0.6444444 1.0000000 1.428571
13 154.0 1.00000000 0.55357143 0.44642857 0.6987952 1.0000000 1.553571
14 155.0 1.00000000 0.60714286 0.39285714 0.7250000 1.0000000 1.607143
15 155.5 0.98275862 0.62500000 0.37500000 0.7307692 0.9722222 1.607759
16 156.0 0.98275862 0.64285714 0.35714286 0.7402597 0.9729730 1.625616
17 157.0 0.96551724 0.67857143 0.32142857 0.7567568 0.9500000 1.644089
18 158.0 0.96551724 0.69642857 0.30357143 0.7671233 0.9512195 1.661946
19 159.0 0.94827586 0.76785714 0.23214286 0.8088235 0.9347826 1.716133
20 160.0 0.93103448 0.76785714 0.23214286 0.8059701 0.9148936 1.698892
21 161.0 0.86206897 0.87500000 0.12500000 0.8771930 0.8596491 1.737069
22 162.0 0.79310345 0.89285714 0.10714286 0.8846154 0.8064516 1.685961
23 163.0 0.77586207 0.92857143 0.07142857 0.9183673 0.8000000 1.704433
24 164.0 0.72413793 0.96428571 0.03571429 0.9545455 0.7714286 1.688424
25 165.0 0.68965517 0.96428571 0.03571429 0.9523810 0.7500000 1.653941
26 166.0 0.62068966 0.98214286 0.01785714 0.9729730 0.7142857 1.602833
27 167.0 0.60344828 1.00000000 0.00000000 1.0000000 0.7088608 1.603448
28 168.0 0.55172414 1.00000000 0.00000000 1.0000000 0.6829268 1.551724
29 169.0 0.51724138 1.00000000 0.00000000 1.0000000 0.6666667 1.517241
30 170.0 0.39655172 1.00000000 0.00000000 1.0000000 0.6153846 1.396552
31 171.0 0.25862069 1.00000000 0.00000000 1.0000000 0.5656566 1.258621
32 172.0 0.22413793 1.00000000 0.00000000 1.0000000 0.5544554 1.224138
33 173.0 0.17241379 1.00000000 0.00000000 1.0000000 0.5384615 1.172414
34 174.0 0.15517241 1.00000000 0.00000000 1.0000000 0.5333333 1.155172
35 175.0 0.13793103 1.00000000 0.00000000 1.0000000 0.5283019 1.137931
36 176.0 0.08620690 1.00000000 0.00000000 1.0000000 0.5137615 1.086207
37 177.0 0.06896552 1.00000000 0.00000000 1.0000000 0.5090909 1.068966
38 180.0 0.03448276 1.00000000 0.00000000 1.0000000 0.5000000 1.034483You can make exploratory plot of sensitivity and specificity. First, You have to transform the data in long from.
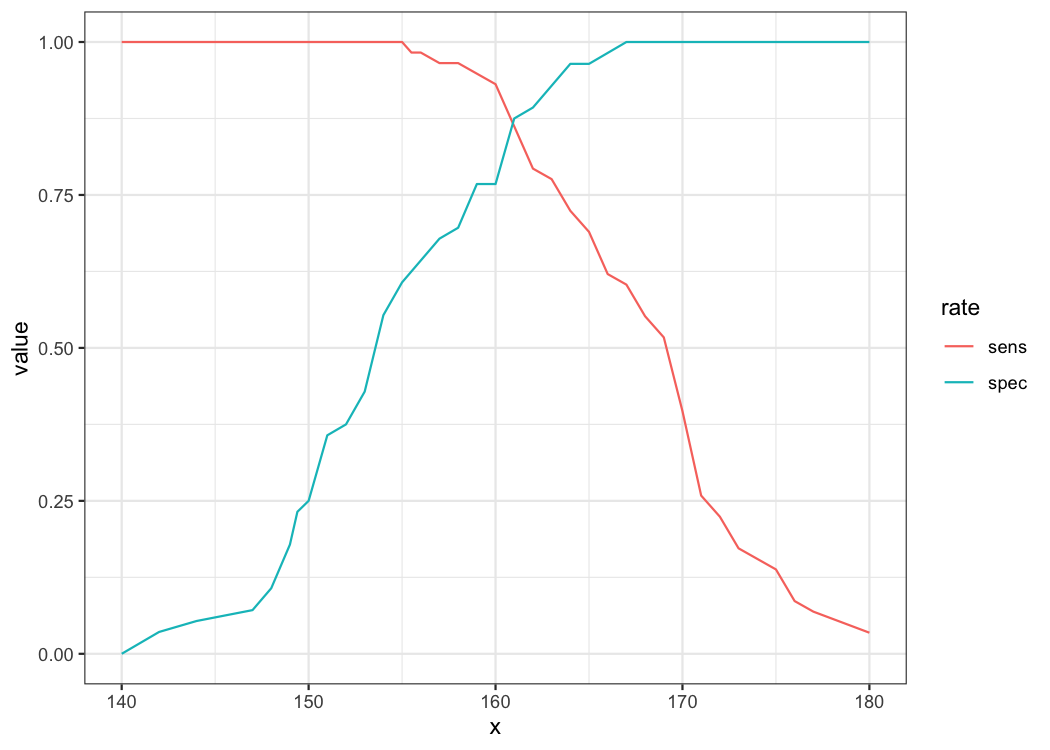
longdf <- result %>% pivot_longer(cols=sens:spec,names_to = "rate")
ggplot(data=longdf,aes(x=x,y=value,color=rate))+geom_line()
As you can see, the higher the sensitivity, the lower the specificity. The optimal cutoff value is determined where the sum of specificity and sensitivity is the highest.
result[which.max(result$sum),]
x sens spec fpr ppv npv sum
21 161 0.862069 0.875 0.125 0.877193 0.8596491 1.737069You can see when the height is 161cm, the sum of sensitivity and specificity is the highest. So the best cutoff value of height is 161cm. With the result, you can draw the ROC plot.
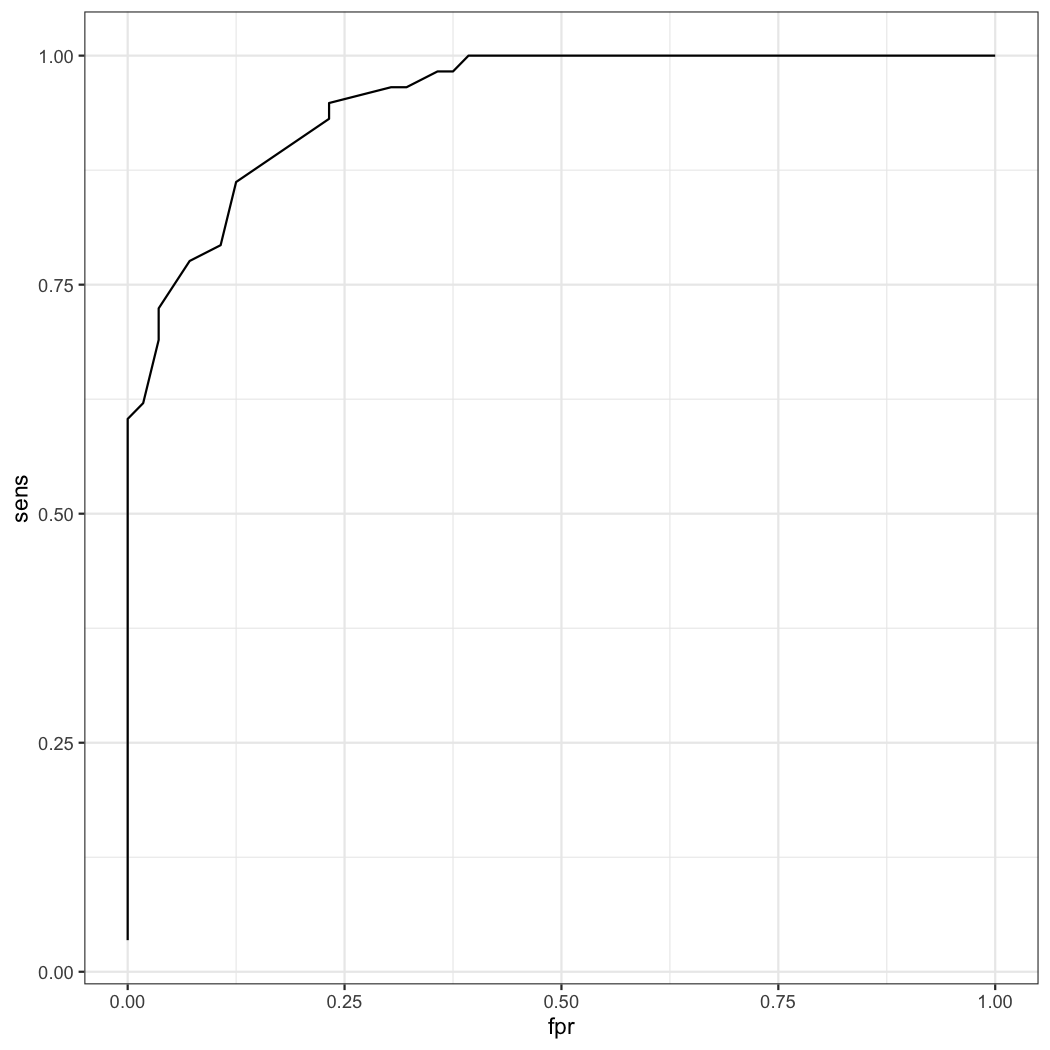
result=result[order(result$sens),]
ggplot(data=result,aes(x=fpr,y=sens))+geom_line()
Look at the first ROC plot again. In the ROC plot, you can see the cutoff value of lr.eta is 0.545. Where does this value come from? This value comes from the generalized linear model.
fit=glm(male~height,data=radial,family=binomial)
fit$fitted.values
1 2 3 4 5 6 7 8
0.0647799156 0.0089609908 0.5450612249 0.1902888834 0.7301078853 0.0134046841 0.8593140964 0.2609731323
9 10 11 12 13 14 15 16
0.9688855513 0.1131501263 0.8593140964 0.9972179420 0.0134046841 0.0059814642 0.9790755722 0.6428952491
17 18 19 20 21 22 23 24
0.9688855513 0.0089609908 0.9790755722 0.0059814642 0.0440658619 0.0039886420 0.9539663976 0.9859766507
25 26 27 28 29 30 31 32
0.0134046841 0.8593140964 0.4436202683 0.9906234843 0.9906234843 0.8593140964 0.9688855513 0.5450612249
33 34 35 36 37 38 39 40
0.9688855513 0.4436202683 0.9987659427 0.0440658619 0.9972179420 0.0059814642 0.5450612249 0.4436202683
41 42 43 44 45 46 47 48
0.4436202683 0.0440658619 0.3466721723 0.5450612249 0.4436202683 0.9323927854 0.0297645408 0.0297645408
49 50 51 52 53 54 55 56
0.9790755722 0.9790755722 0.7301078853 0.9688855513 0.7301078853 0.9937403001 0.9790755722 0.0011789400
57 58 59 60 61 62 63 64
0.1352457877 0.9539663976 0.7301078853 0.0059814642 0.7301078853 0.0134046841 0.9996359536 0.9790755722
65 66 67 68 69 70 71 72
0.6428952491 0.4436202683 0.1352457877 0.0942707968 0.0647799156 0.5450612249 0.9906234843 0.9017500029
73 74 75 76 77 78 79 80
0.9859766507 0.2609731323 0.9981468171 0.4436202683 0.6428952491 0.9996359536 0.0005224834 0.2609731323
81 82 83 84 85 86 87 88
0.4436202683 0.9688855513 0.4436202683 0.9017500029 0.0440658619 0.8593140964 0.9323927854 0.0002314699
89 90 91 92 93 94 95 96
0.9972179420 0.0297645408 0.8025624552 0.9958254317 0.0647799156 0.9790755722 0.0089609908 0.0048849508
97 98 99 100 102 103 104 105
0.0105295308 0.0134046841 0.0440658619 0.9688855513 0.0942707968 0.0200074872 0.0440658619 0.8025624552
106 107 108 109 110 111 112 113
0.9790755722 0.4436202683 0.9987659427 0.0440658619 0.0134046841 0.0002314699 0.1352457877 0.2609731323
114 115
0.2609731323 0.9323927854 You can see the fitted mean values, obtained by transforming the linear predictors by the inverse of the link function. You can use this value to make a ROC plot. Again, you can use calSens() function.
result2=calSens(fit$fitted.values,fit$y)
result2[which.max(result2$sum),]
x sens spec fpr ppv npv sum
21 0.5450612 0.862069 0.875 0.125 0.877193 0.8596491 1.737069The optimal fitted value is 0.5451. You can draw ROC curve with this value.
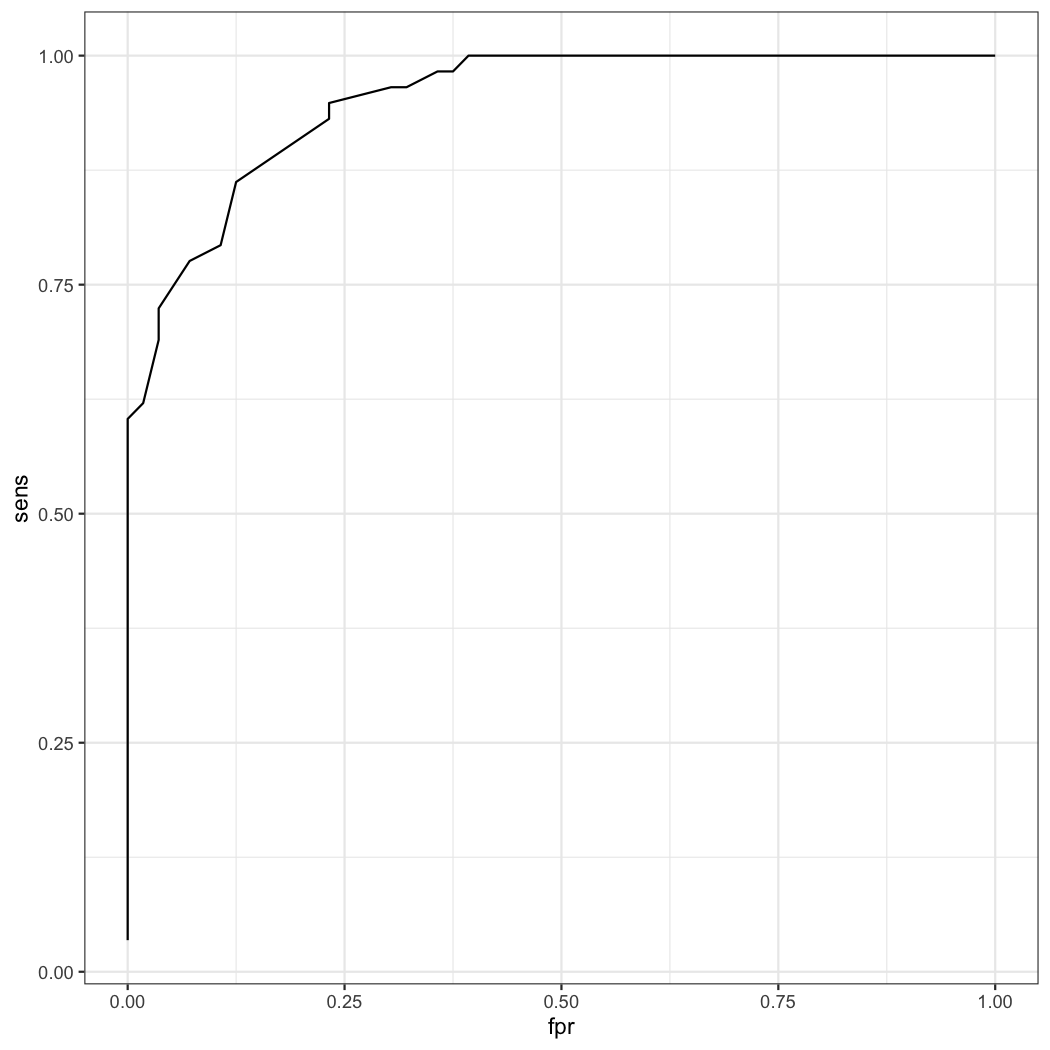
result2=result2[order(result2$sens),]
ggplot(data=result2,aes(x=fpr,y=sens))+geom_line()
What is the relationship of the fitted value of 0.5451 and height 161cm ? As you knows, you can interpretate the logistic equation as follows.
\begin{equation} log(\frac{p}{1-p})=\beta_0+\beta_1*X \end{equation}
This equation is expressed with the following R command.
qlogis(x$cutpoint)=coef(x$fit)[1]+coef(x$fit)[2]*X
So you can calculate the optimal cutpoint of height with the optimal fitted value 0.5451 as follows.
height=(qlogis(x$cutpoint)-unname(coef(x$fit)[1]))/unname(coef(x$fit)[2])
height
[1] 161In the lower right corner, you can see the area under curve(AUC) and the p value from Wilcoxon Rank Sum test. The p value comes from:
wilcox.test(radial$height,radial$male)
Wilcoxon rank sum test with continuity correction
data: radial$height and radial$male
W = 13110, p-value < 2.2e-16
alternative hypothesis: true location shift is not equal to 0The AUC is calculated by the simpleAUC function included in multipleROC package.
simpleAUC <- function(df){
df=df[order(df$x,decreasing=TRUE),]
TPR=df$sens
FPR=df$fpr
dFPR <- c(diff(FPR), 0)
dTPR <- c(diff(TPR), 0)
sum(TPR * dFPR) + sum(dTPR * dFPR)/2
}
simpleAUC(x$df)
[1] 0.9510468You can convert a multipleROC object to a roc object. You can use this object to calculate auc or compare the AUC of two ROC curves.
class(x)
[1] "multipleROC"
multipleROC2roc=function(x){
pROC::roc(x$fit$y,x$fit$fitted.values,ci=T)
}
x2 <- multipleROC2roc(x)
class(x2)
[1] "roc"
pROC::auc(x2)
Area under the curve: 0.951You can draw multiple ROC curves in the same plot. First, make a list of multipleROC objects and use the plot_ROC function.
a=multipleROC(male~height,data=radial,plot=FALSE)
b=multipleROC(male~age,data=radial,plot=FALSE)
c=multipleROC(form=male~weight,data=radial,plot=FALSE)
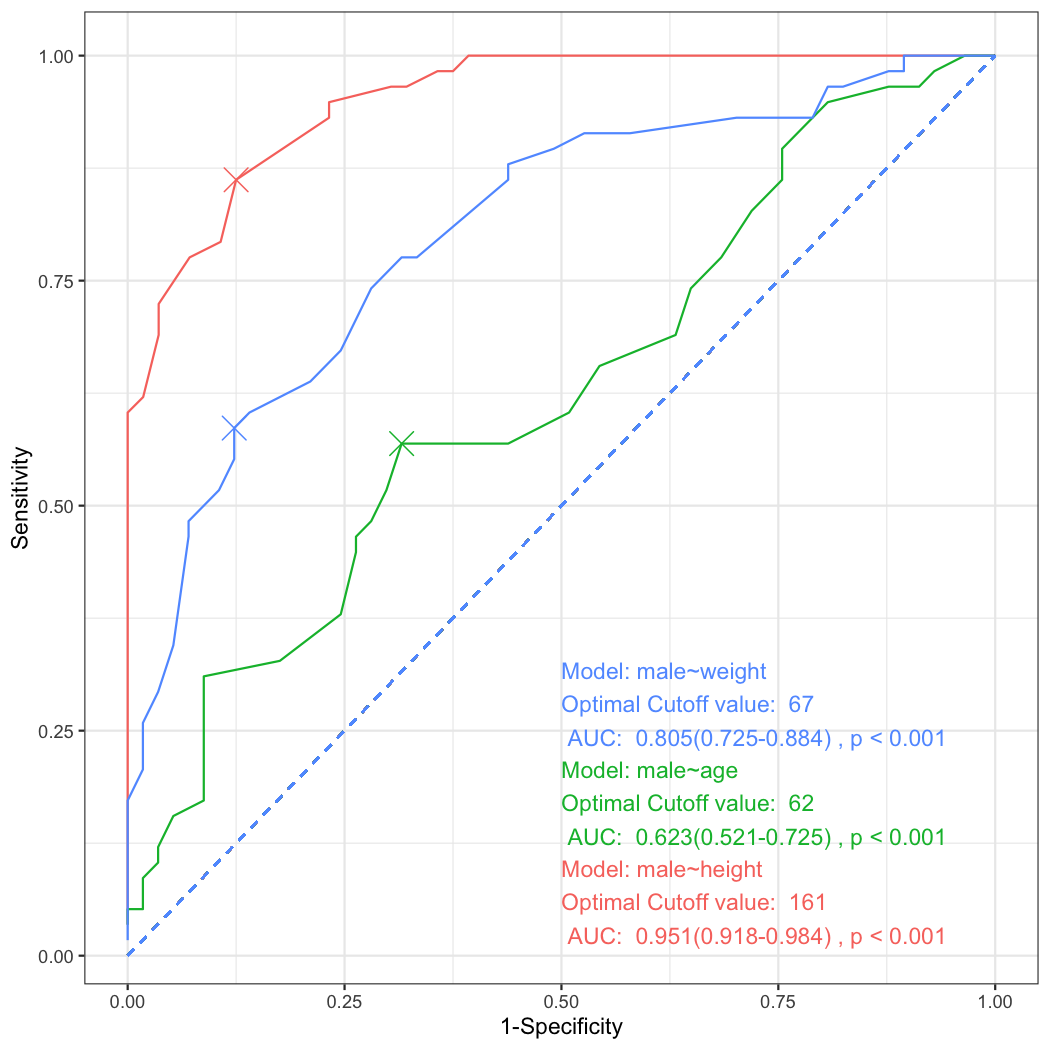
plot_ROC(list(a,b,c),show.eta=FALSE,show.sens=FALSE)
You can make facetted plot with the following R command.
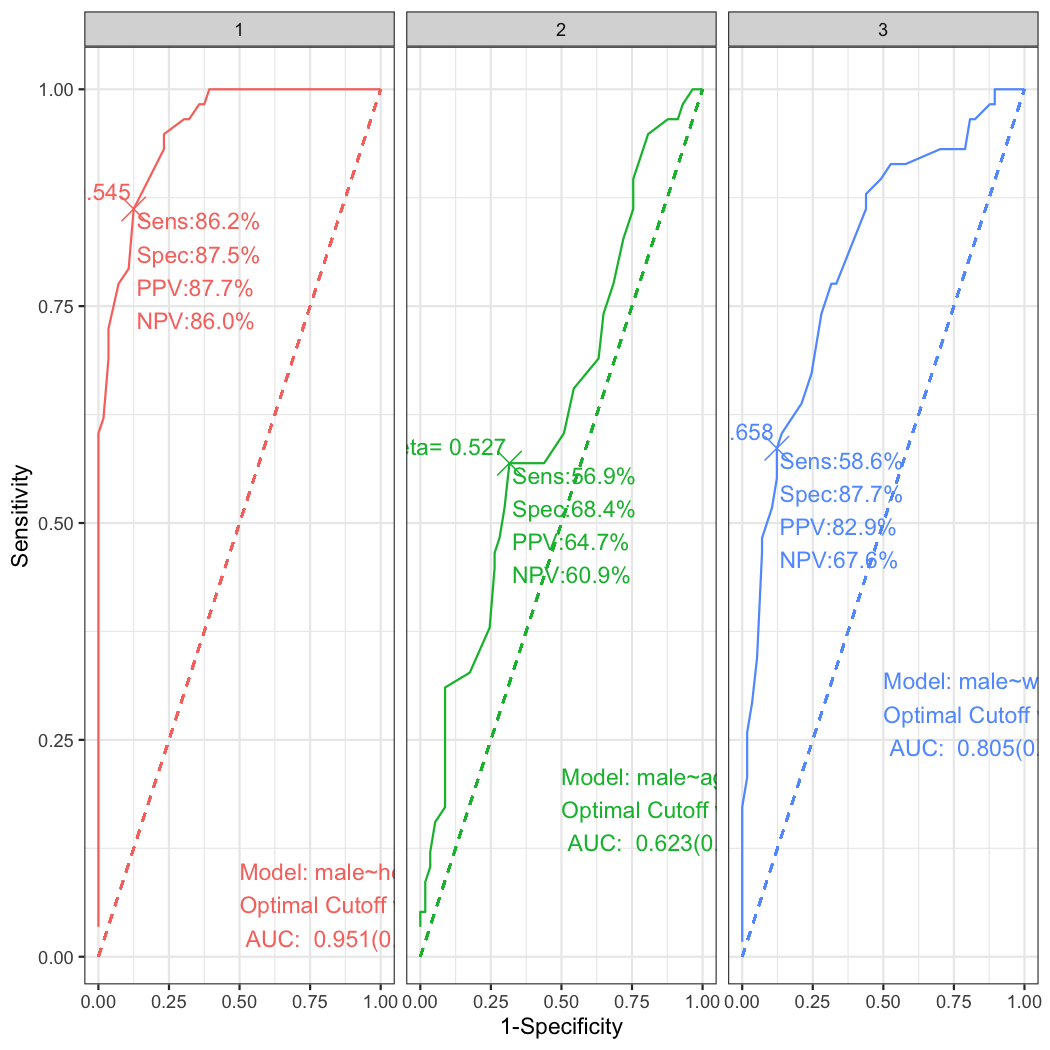
plot_ROC(list(a,b,c),facet=TRUE)
By setting the facet argument TRUE, you can get the facetted plot. Alternatively you can use the facet_grid() function of the package ggplot2.
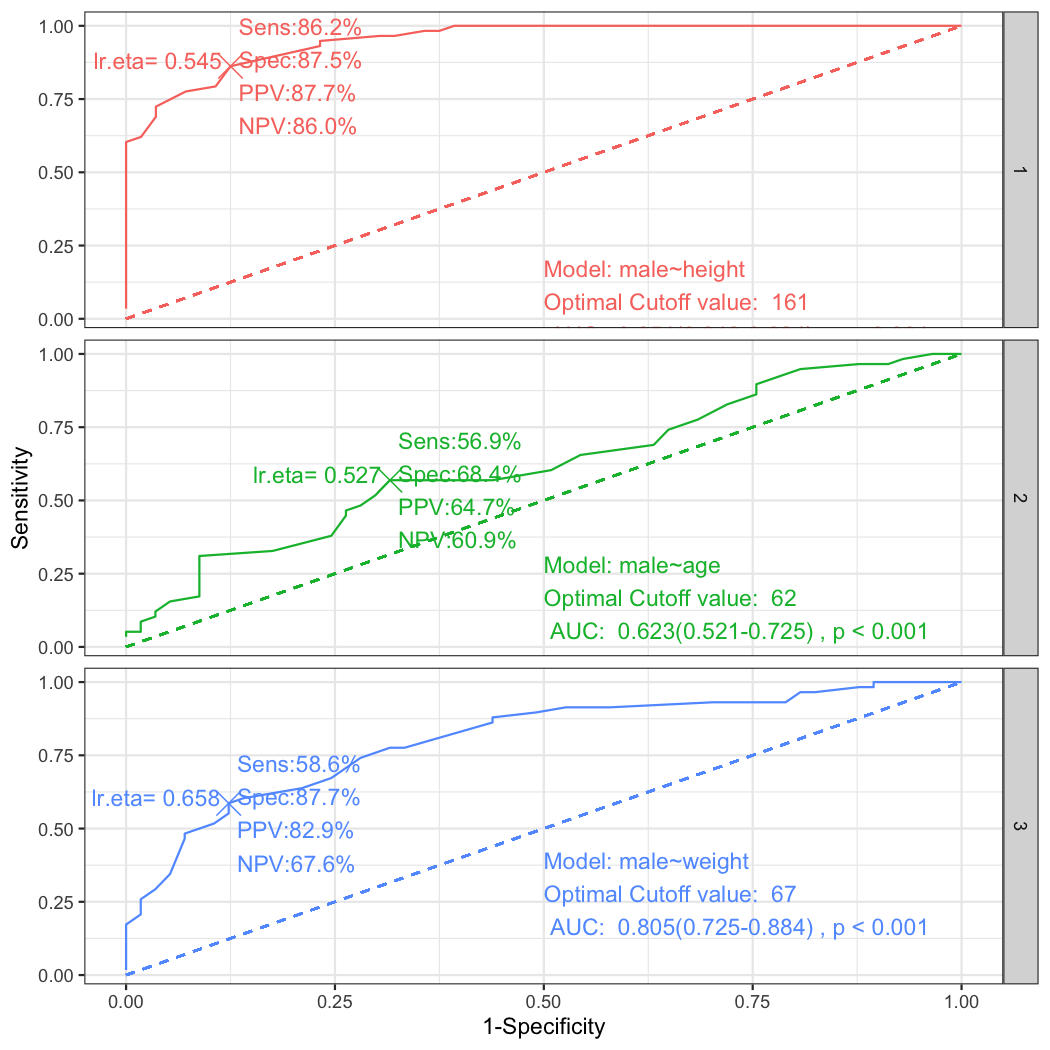
require(ggplot2)
plot_ROC(list(a,b,c))+facet_grid(no~.)
You can make ROC plots with multiple predictors.
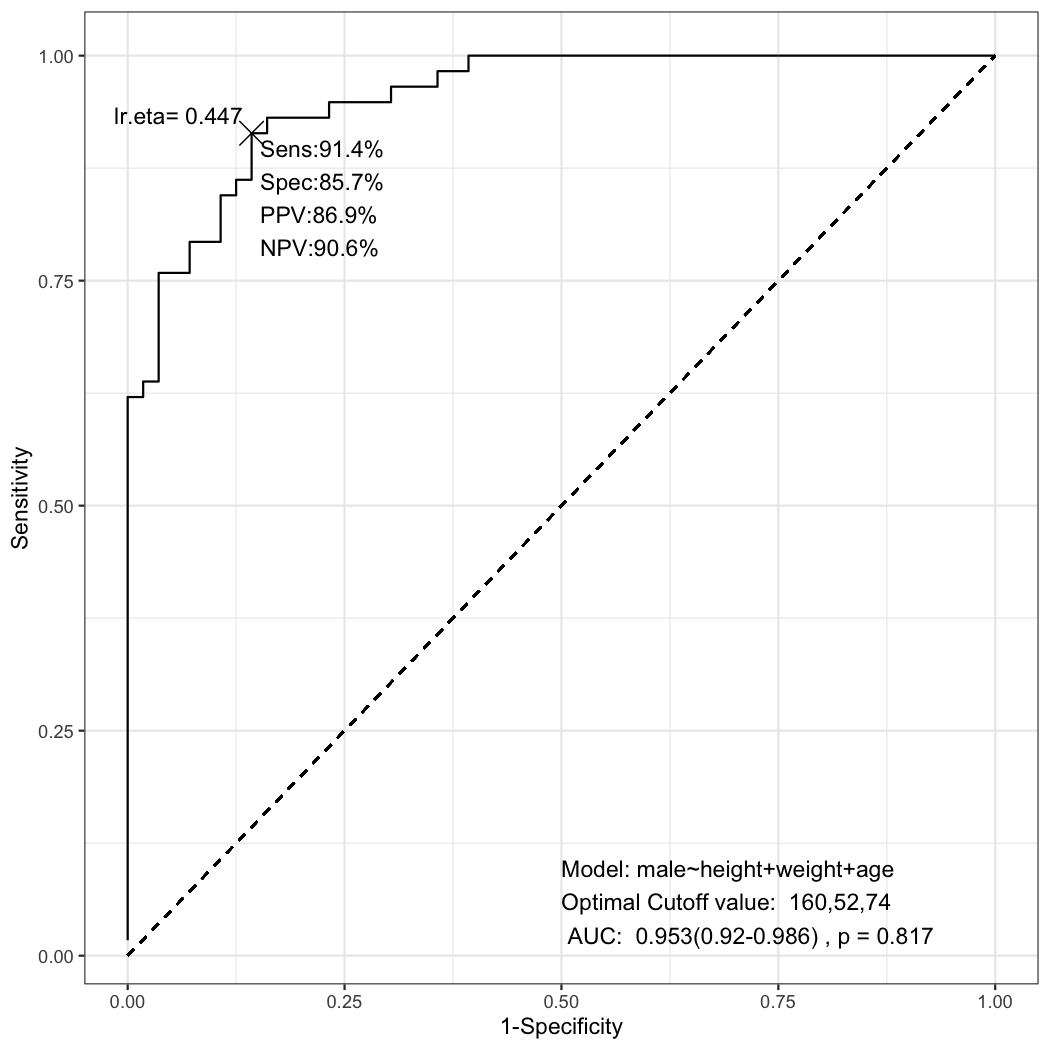
multipleROC(male~height+weight+age,data=radial)
This plot is made from the following glm object.
fit=glm(male~height+weight+age,data=radial,family=binomial)You can use automatic stepwise backward elmination by AIC in multiple glm model.
final=step(fit,trace=0)
summary(final)
Call:
glm(formula = male ~ height, family = binomial, data = radial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.15418 -0.30022 0.02699 0.25143 2.17328
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -65.38126 12.72530 -5.138 2.78e-07 ***
height 0.40722 0.07918 5.143 2.71e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 158.002 on 113 degrees of freedom
Residual deviance: 63.462 on 112 degrees of freedom
(1 observation deleted due to missingness)
AIC: 67.462
Number of Fisher Scoring iterations: 6You can compare the initial and final model.
anova(final,fit,test="Chisq")
Analysis of Deviance Table
Model 1: male ~ height
Model 2: male ~ height + weight + age
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 112 63.462
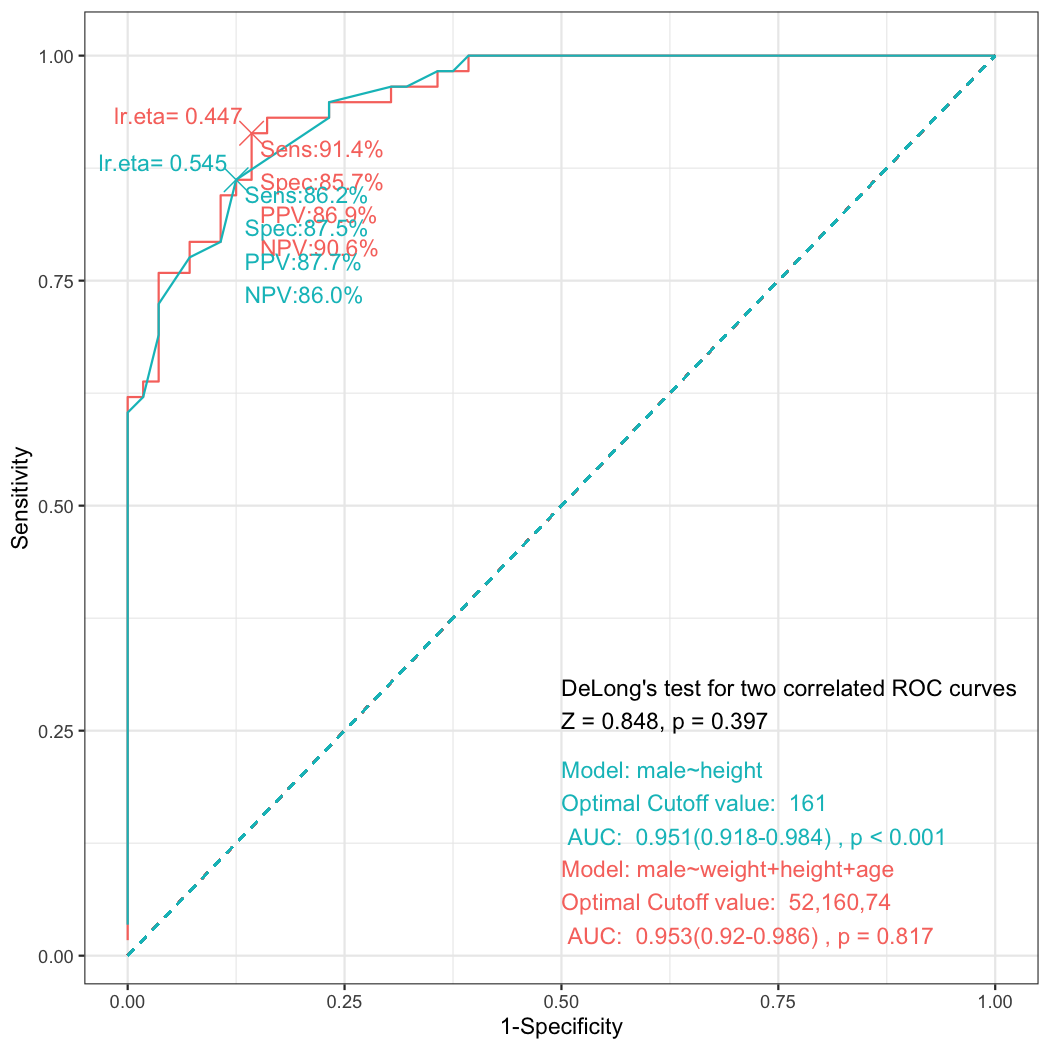
2 110 63.352 2 0.11025 0.9464You can draw plot comparing two ROC curves of the initial and the final model.
step_ROC(male~weight+height+age,data=radial)
You can get the anova table.
step_ROC(male~weight+height+age,data=radial,plot=FALSE)
Analysis of Deviance Table
Model 1: male ~ height
Model 2: male ~ weight + height + age
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 112 63.462
2 110 63.352 2 0.11025 0.9464