Mirage is a tensor algebra superoptimizer that automatically discovers highly-optimized tensor programs for DNNs. Mirage automatically identifies and verifies sophisticated optimizations, many of which require joint optimization at the kernel, thread block, and thread levels of the GPU compute hierarchy. For an input DNN, Mirage searches the space of potential tensor programs that are functionally equivalent to the DNN to discover highly-optimized candidates. This approach allows Mirage to find new custom kernels that outperform existing expert-designed ones.
The quickest way to try Mirage is through our prebuilt docker images. You can also install Mirage from source.
As a tensor algebra superoptimizer, Mirage can be used to optimize arbitrary DNNs. We use two examples to show how to use Mirage to automatically generate CUDA kernels for group-query attention (GQA) in LLAMA-3-70B and low-rank adapter (LoRA). These Mirage-generated kernels outperform existing manually-optimized kernels.
The follow code snippet shows how to use Mirage to automatically generate highly-optimized CUDA programs for group-query attention (GQA) in LLAMA-3-70B. We assume the model is served in half precision and is tensor model parallelized across 4 GPUs to fit in GPU device memory. Therefore, the GQA operator computes attention across 8 query heads and 2 key-value heads.
First, we define the computation graph for GQA, which takes three input tensors Q, K, and V, and produces a single output tensor O that contains the attention result:
import mirage as mi
graph = mi.new_graph()
Q = graph.new_input(dims=(2, 256, 64), dtype=mi.float16)
K = graph.new_input(dims=(2, 64, 4096), dtype=mi.float16)
V = graph.new_input(dims=(2, 4096, 64), dtype=mi.float16)
A = graph.matmul(Q, K)
E = graph.exp(A)
S = graph.reduction(E, 2)
D = graph.div(E, S)
O = graph.matmul(D, V)Second, we will use mi.superoptimize to superoptimize GQA. Mirage will automatically search the space of potential mugraphs that are functionally equivalent to the input graph to discover highly-optimized CUDA programs. MuGraphs are a new multi-level graph representation in Mirage that specifies computation at the kernel, thread block, and thread levels of the GPU compute hierarchy. Mirage can automatically find mugraphs that represent today's expert-designed GPU optimizations such as FlashAttention, FlashDecoding, and FlashInfer. In addition, Mirage also discovers other mugraphs that outperform these expert-designed implementations for certain cases.
new_graphs = mi.superoptimize(graph, griddims=[(2, 16, 1), (2, 16, 4)])The search is configured by several parameters, among which griddims is the one you are likely to reset for your problem sizes. The default values for these parameters are tailored for multi-head, multi-query, and group-query attention. You can update them to superoptimize other neural architectures such as low-rank adapters, mixture-of-experts, and more. A more detailed definition for these parameters is available in our paper.
griddims: specify the possible number of thread blocks within a kernel. Default (for multi-head attention with 16 heads per GPU):(16, 1, 1), (16, 2, 1), (16, 4, 1).blockdims: specify the possible number of threads within a thread block. Default:(128, 1, 1).imaps: potential mappings between data dimensions of an input tensor andgriddims. Default (for all attention variants):(0, -1, -1), (0, 1, -1), (0, 2, -1), (0, -1, 1). Note that a positive number indicates the input tensor is partitioned along that grid dimension, while-1indicates the input tensor is replicated (see the paper for details).omaps: potential mappings between data dimensions of an output tensor andgriddims. Default (for all attention variants):(0, -1, -1), (0, 1, -1), (0, 2, -1), (0, 2, 1)]. The semantic is similar toimaps.fmaps: potential mappings between data dimensions of an input tensor and the for-loop dimension of the thread block. Default:-1, 1, 2. Similar toimaps, a positive number indicates the input tensor is partitioned and-1indicates the tensor is replicated.franges: possible for-loop ranges to be considered during the search. Default:1, 4, 8, 16.
Except for griddims, which depends on the problem sizes, the default values for other parameters are sufficient to discover FlashAttn, FlashDecoding, and many other expert-designed implementations for Attention.
The mi.superoptimize function returns a list of mugraphs discovered by Mirage that are functionally equivalent to the input program and represent different implementations of it. Mirage uses a probabilistic equivalence verification mechanism to ensure that all discovered mugraphs are equivalent to the inpout. graph.generate_triton_program generates a Triton program for each mugraph.
for i, mugraph in enumerate(new_graphs):
mugraph.generate_triton_program("generated_program_{}.py".format(i))The above search procedure takes around 4 hours and discovers 69 potential tensor programs for implementing GQA. To bypass the search and directly check the generated programs, we can start from a previous checkpoint of the search by running
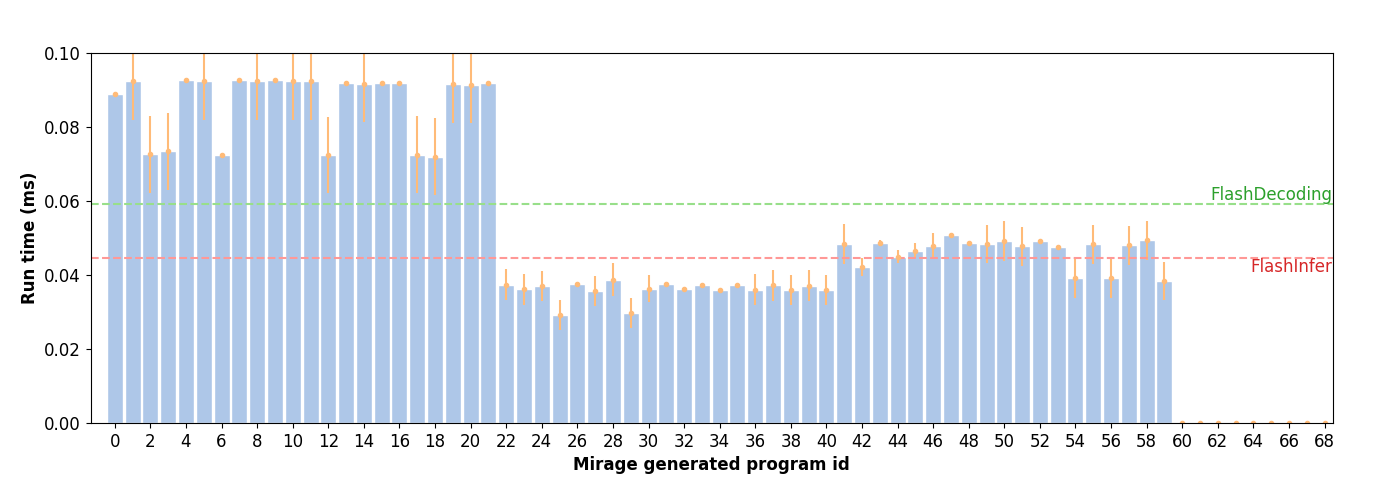
python demo/demo_group_query_attention_spec_decode.py --checkpoint demo/checkpoint_group_query_attn_spec_decode.jsonThis program outputs 69 Triton programs saved in the demo folder. The performance of these programs on a NVIDIA A100 GPU is shown as follows. Note that some generated programs perform small matrix multiplications within a thread block. These programs cannot be directly supported by the current Triton compiler, as it requires all dimensions of a matrix multiplication must be at least 16. The best program discovered by Mirage is 2x faster than FlashDecoding and 1.5x faster than FlashInfer.
A paper describing Mirage's techniques is available on arxiv. Please cite Mirage as:
@misc{wu2024mirage,
title={A Multi-Level Superoptimizer for Tensor Programs},
author={Mengdi Wu and Xinhao Cheng and Oded Padon and Zhihao Jia},
eprint={2405.05751},
archivePrefix={arXiv},
year={2024},
}Mirage uses Apache License 2.0.