/CSCE156-Lab15

Lab 15.0 - CSCE 156

Primary LanguageJava

Computer Science II

Lab 15.0 - Binary Search Trees

School of Computing
College of Engineering
University of Nebraska-Lincoln
University of Nebraska-Omaha

An introduction Binary Search Tree data structures.

Overview

Resources

Prior to lab you should read/review the following resources.

  1. Review this laboratory handout prior to lab.

  2. Review the course material on Binary Search Trees and Heaps

Lab Objectives & Topics

Following the lab, you should:

  • Be familiar with Binary Search Trees and Heaps

  • Be able to implement and utilize tree traversal algorithms

  • Be able to utilize BSTs and Heaps in an application

Peer Programming Pair-Up

To encourage collaboration and a team environment, labs will be structured in a pair programming setup. At the start of each lab, you may be randomly paired up with another student by a lab instructor. One of you will be designated the driver and the other the navigator.

The navigator will be responsible for reading the instructions and telling the driver what is to be done. The driver will be in charge of the keyboard and workstation. Both driver and navigator are responsible for suggesting fixes and solutions together. Neither the navigator nor the driver is "in charge."
Beyond your immediate pairing, you are encouraged to help and interact and with other pairs in the lab.

Each week you should try to alternate: if you were a driver last week, be a navigator next, etc. Resolve any issues (you were both drivers last week) within your pair. Ask the lab instructor to resolve issues only when you cannot come to a consensus.

Because of the peer programming setup of labs, it is absolutely essential that you complete any pre-lab activities and familiarize yourself with the handouts prior to coming to lab. Failure to do so will negatively impact your ability to collaborate and work with others which may mean that you will not be able to complete the lab.

1. Getting Started

Clone this project code for this lab from GitHub in Eclipse using the URL: https://github.com/cbourke/CSCE156-Lab15. Refer to Lab 1.0 for instructions on how to clone a project from GitHub.

2. Tree-Based Data Structures

2.1 Binary Search Trees

A Binary Search Tree (BST) is a data structure such that elements are stored in tree nodes. Each tree node has a reference to its parent, left child, and right child. Each node in a BST also has a key associated with it. The Binary Search Tree Property is such that:

  1. All keys in a node's left-subtree are less than that node's key

  2. All keys in a node's right-subtree are greater than that node's key

An example:

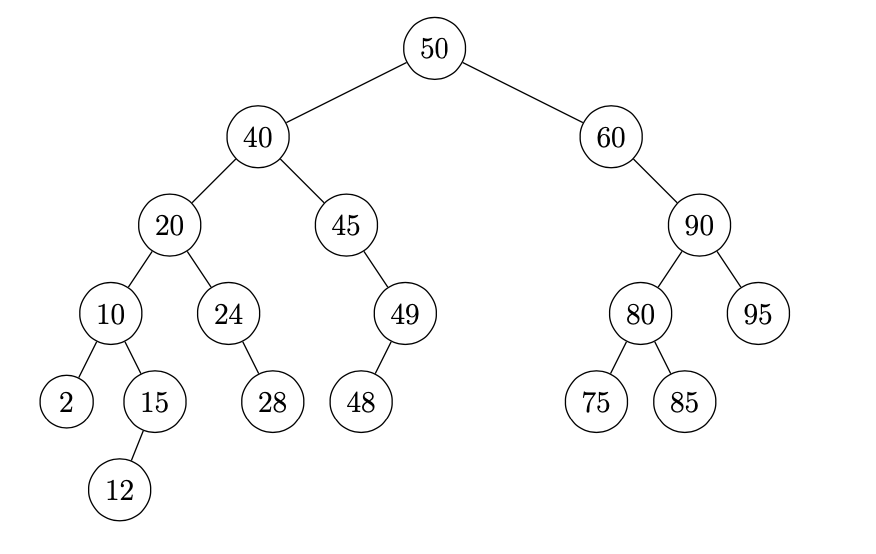
Binary Search Tree

The basic functionality such as adding elements, searching for elements, and removing elements can be implemented with a complexity proportional to the tree's depth. Searching, for example, starts at the root. If the node corresponds to the element we are searching for we are done. Otherwise, if the node has a key value less than the element we are searching for we traverse to its right child. If the node has a key value greater than the element we are searching for we traverse to its left child and repeat until we have found the node or we reach the end of a tree without finding our element.

An incomplete binary search tree Java implementation has been provided for you. It has some basic functionality already. Your activities will include adding additional methods to perform a search, and to traverse the tree using several different traversal strategies and to count the number of leaves in the tree.

A node in a binary tree is called a leaf if it has no children. Since the structure of a binary search tree is determined by the order elements are entered, there is no easily computable formula for the number of leaves. Instead, a BST needs to be traversed and the leaves counted up.

There are three traversal strategies that you will implement. The implementation details are left up to you. You may find that a recursive strategy is the quickest to implement or you may find a stack data structure useful. Each of these strategies begins at the root and visits a node and its children in different orders.

  • Preorder Traversal: processes the node, then visits the nodes in the left-subtree then in the right-subtree

  • Inorder Traversal: visits the left-subtree first, then the node itself, then the right-subtree

  • Postorder Traversal: visits the left-subtree first, then the right- subtree, then the node itself

2.2 Heaps

A heap is a data structure similar to a binary search tree in that it has a binary tree structure. The primary difference is that the key for each node in the tree is larger than both of its children. There is no restriction on the relation between the keys of child nodes. Another condition of heaps is that they are full binary trees: each level of the tree, with the possible exception of the final row has every node present. This property ensures that operations such as add and remove (from the top) can be performed with $O(\log(n))$ operations.

A heap can be implemented using a dynamic array. The random access ensures the optimal behavior of operations because the left and right children (and parent) of each node has an easily computable relationship using indices. We won't be implementing a heap directly, instead we'll use Java's PriorityQueue which is a basic (binary) heap implementation. We'll use this data structure to implement a heap sort algorithm.

The basic idea is that elements are removed from a input list one-by-one and are placed on a heap. Then, elements are successively removed from the heap and placed back into the list. The heap property guarantees that the maximal (or minimal) element is removed each time, imposing an ordering.

3. Activities

3.1 Binary Search Tree Implementation

  1. Implement the search algorithm described above (the findElement() method)

  2. Implement the inorder and post order methods. The preorder method has been done for you as an example and a non-recursive, stack-based version has also been provided.

  3. Implement the getNumLeaves() method

3.2 Heap Sort Implementation

  1. Refer to the PriorityQueue documentation, https://docs.oracle.com/en/java/javase/15/docs/api/java.base/java/util/PriorityQueue.html for how to use it.

  2. Use this implementation to implement the heapSort() method in the HeapSort class.

4. Testing, Submitting & Grading

  • Test your programs using the provided JUnit test suite(s). Fix any errors and completely debug your programs.
  • Submit the following files through webhandin:
    • BinarySearchTree.java
    • HeapSort.java
  • Run the grader and verify the output to complete your lab.

Advanced Activity (optional)

Another tree traversal strategy is a Breadth-First-Search (BFS) traversal strategy. Starting at the root, nodes are visited level-by-level in a left-to-right order. Design (or research) and implement a BFS strategy on your binary search tree. Hint: look at the non-recursive traversal strategies used in some of the methods provided to you. Think of a similar strategy using a different data structure.