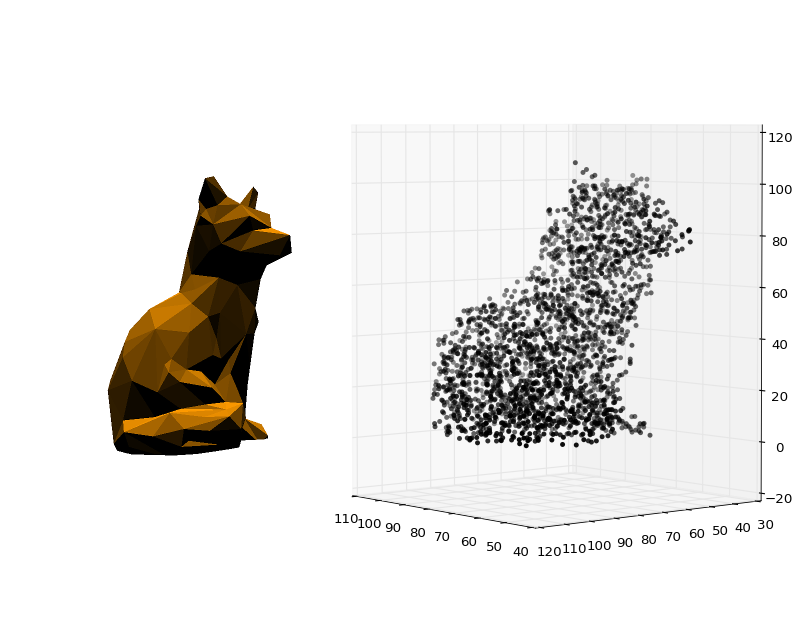
This project demonstrates a short Python function to determine if a set of points are inside or outside a 3d mesh. The 3d mesh is assumed to be made of triangles which all have the same orientation. This function manages to be short yet robust and reasonnably fast. No preprocessing of the mesh is required.
The implementation is using the Generalized Winding Number of a 3d mesh, a concept introduced in the paper Robust Inside-Outside Segmentation using Generalized Winding Numbers by Alec Jacobson, Ladislav Kavan and Olga Sorkine-Hornung.
You will need
- A Unix-ish environment
- Python 2.7 or Python 3.x
- Numpy
- Matplotlib
- The xz compression suite
- The actual point inside/outside mesh test is in the is_inside_mesh.py
file. Two implementations are available : naive and turbo.
- naive is as straighforward and unsophisticated as I could make it, for didactic purposes.
- turbo is optimized for speed (vectorized computations) and is flexible about the floating point precision used for the computation.
- demo-naive.py is a demo for the naive implementation
- demo-turbo.py is a demo for the optimized implementation
- cube-test.py is a unit test that illustrates accuracy issues due to the arctan2 function.
- stlparser.py is a parser for ASCII STL files
Both demos
- load an ASCII STL file (a file format for 3d triangle mesh) from the standard input
- generates an uniform random sampling of the volume enclosed by the mesh
- displays the samples
Using one the sample STL files provided with the naive implementation demo
xzcat meshes/fox.stl.xz | python demo-naive.py
Likewise, for the optimized implementation demo
xzcat meshes/fox.stl.xz | python demo-turbo.py
The call to the function arctan2 is hurting the accuracy of the test. All the other operations could be done with high accuracy/robustness using fancy summation algorithms.
To enable higher accuracy with the is_inside_turbo implementation of the test, simply pass the triangles as an array with the longdouble type, ie. 128 bits floating point numbers, using the astype method of Numpy arrays.
The naive implementation is a straight translation of the Generalized Winding Number definition.
The optimized implementation uses a couple of tricks
- Vectorization : the winding number of all the points to test is accumulated per triangle, using Numpy vector operations. This allows to offload most of the computations to compiled and optimized code.
- The 3x3 determinant is computed explicitly, so that it can be vectorized and because Numpy's implementation is trading speed for robustness.
The arctangent is not computed, as it is not required when for an inside/outside test.Actually, I believe an arctangent computation can be avoided, but I'm not sure how. That would be both a gain in term of accuracy and speed.
Using the Generalized Winding Number for a inside/outside test is not optimal. It takes O(n) operations for n triangles, while a raycasting approach takes O(log(n)) operations when a suitable data structure such as a KD-tree is used. However, the raycasting approach usually requires more code and takes more efforts to make it robust to degenerate cases. In contrast, the Generalized Winding Number approach can handles holes, non-manifold surfaces and duplicated triangles without code for special case handling.
The Generalized Winding Number is naturally parallel, it is the same computation repeated for each triangle and each point to test. This make this approach a natural fit for a vectorized, multi-core implementation or a GPU implementation.
- Alexandre Devert - Initial work - marmakoide
- Thanks to Guy Rapaport to suggest the cube test case with a sample implementation
This project is licensed under the MIT License - see the LICENSE.md file for details