Koelsynth is a simple, real-time, music audio synthesis library. Its core is written in C++, and it is interfaced with Python using pybind11.
Right now, it supports the following:
- An ADSR envelope generator
- An FM synthesis based audio generator
- An audio sequencer that can mix audio streams from multiple events in real-time
It does not handle any of the following:
- Mapping of frequencies based on a scale
- Generation of melodies or chords
- Playing audio
This is the envelope that we will apply on the top of the audio generated by each event. ADSR stands for Attack, Decay, Sustain, and Release. Let me explain it in my own words. First, stare at the following image for some time.
Imagine a simple, keyboard-based synthesizer. When we press a key (key-down trigger), it triggers the audio. First is the attack phase, where audio energy goes from 0 to a peak value. Then comes the decay phase, where the initial storm of sound madness settles to a lower sound level. Then it either remains at the same level or slowly decays to a lower level until we release the key (key-up trigger). Release of the key triggers the release phase where the energy of the audio returns back to 0.
This is more or less what Koelsyth does. Note that Koelsynth does not handle two triggers for every key. There is no way to communicate the release of a key to the sequencer (at least for now). The initial trigger has to provide the 'sustain duration' for the audio event. This is sub-optimal for triggering audio using a keyboard. But I have no skills in that and my interest is in algorithmic generation of melodies and music in general.
The following are the ADSR parameters:
- timing related (duration in number of samples, integer)
- attack
- decay
- sustain
- release
- level related (between 0 and 1, float)
- slevel1: starting level of sustain (ending level of decay)
- slevel2: ending level of sustain (starting level of release)
The simplest music audio synthesis we can do is with a single tone. But it doesn't sound great. We will have to add more harmonics and make sure that the higher harmonics die faster than the lower ones. For example, here is the spectrogram of a piano's sound, showing the behavior of harmonics.
We can simulate such behavior by adding decay to harmonics to obtain a music sound. This approach is called additive synthesis. I tried that once and it wasn't that great.
Next, there is "subtractive" synthesis (not really a surprise after "additive" synthesis, is it?). It involves taking a waveform with many harmonics (triangular wave, sawtooth wave, etc) and using a time-varying filter to remove the higher harmonics. I tried that too once, but it wasn't great either, at least for the effort involved in coding and tweaking the parameters.
Then I came across FM Synthesis. This turned out to work rather well, compared to the effort involved. I have included this in Koelsyth.
FM stands for Frequency Modulation. Koelsynth currently provides a very basic FMSynth generator. I will explain the theory before getting into the parameters. (Note: I don't have a clear source for reference, unfortunately. If I find one, I will update this section later).
Let's start with a simple sine wave in the discrete domain (integer n instead of real-valued t):
y[n] = sin(2 π f n)
Here f is the frequency relative to sampling frequency: f = f_continuous / sample_rate.
Our aim is to modulate the frequency f in a time-dependent way. We need f[n] instead of a constant f. If we are not careful, we will end up with junk here. The sin wave works on phase changes. So we have to modify the equation as follows, taking care of phase updates based on changing frequency. I will use θ[n] to denote the phase.
# This will give junk
y[n] = sin(2 π f[n] n)
# But this will work
θ[n] = θ[n-1] + 2 π f[n]
y[n] = sin(θ[n])
Now the question is how to "modulate" f[n]. In FM radio communication, a message signal, typically of max-frequency much lower than a carrier is used. Then f[n] takes the following form:
f[n] = c + β m[n]
Where c is the carrier frequency, m[n] is the amplitude of the message (like speech or music), and β is the modulation constant. Note that the audio frequency limit is usually below 20kHz and the carrier frequency could be in MHz range. The carrier oscillates much faster than the variations in the message signal. However, this is not the case in FM synthesis used for music sound generation. The modulating signal usually has several times the frequency of the base signal. I will use g for the tone frequency (relative to sample_rate), i for an integer, typically in the range 1 <= i <= 20, and (g x i) for an integer multiple of tone frequency.
m[n] = sin(2 π (g x i) n) # modulating signal
f[n] = g (1 + β m[n]) # instantaneous frequency
θ[n] = θ[n-1] + 2 π f[n] # phase accumulation
y[n] = sin(θ[n]) # final result
In the above, the depth of modulation is constant. But to get a more realistic sound, we will need to have a high modulation at the start, and then slowly reduce that over time. This can be done with the help of an ADSR envelope. Let's call it the "modulation envelope" (e[n]). The final waveform also needs an envelope. We will use E[n] for that. With these included, we will have the following set of updates.
m[n] = sin(2 π (g x i) n) # modulating signal
f[n] = g (1 + β m[n] e[n]) # instantaneous frequency
θ[n] = θ[n-1] + 2 π f[n] # phase accumulation
y[n] = sin(θ[n]) E[n] # final result
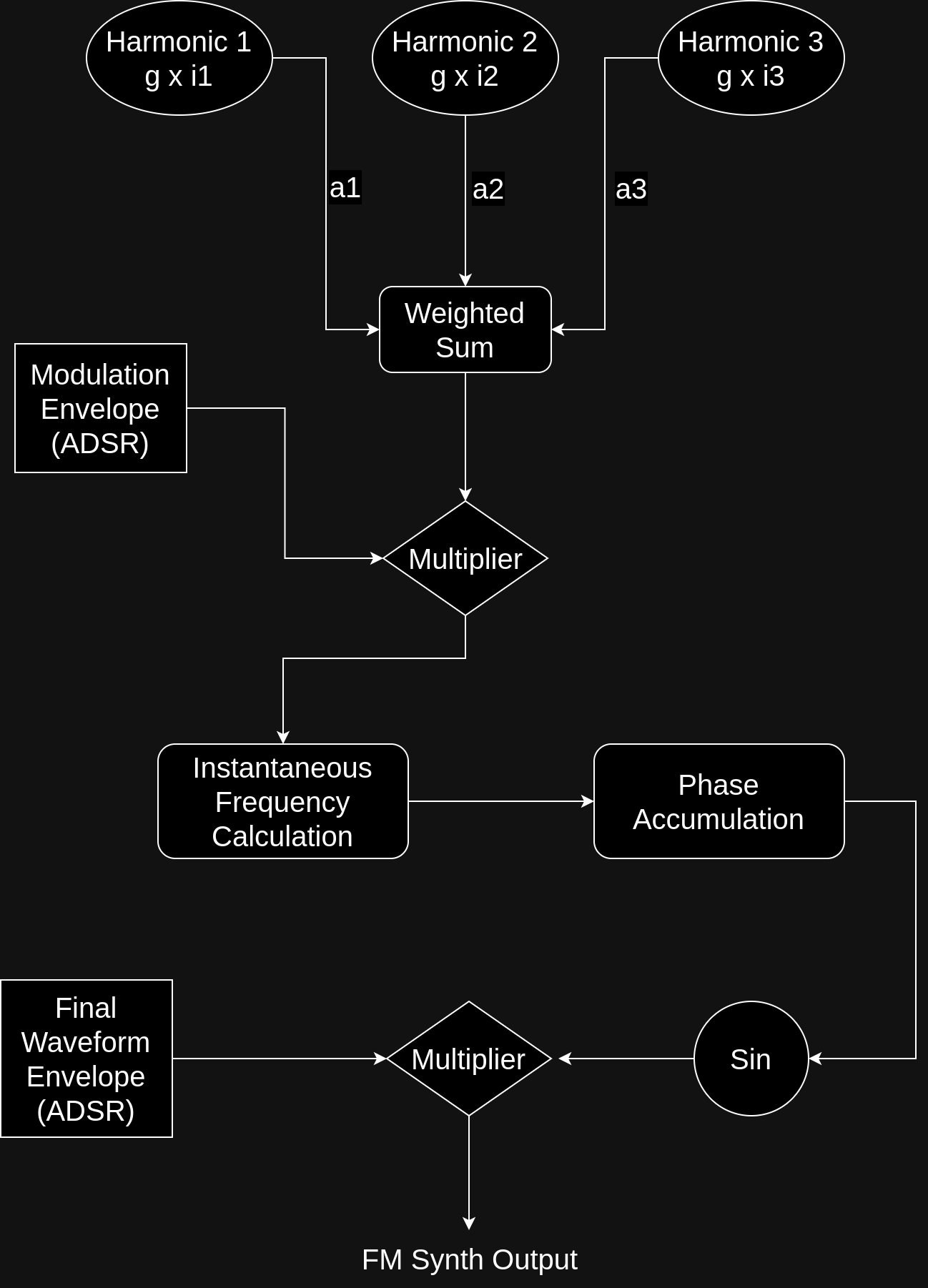
This can be improved further by having multiple modulating components with multiple frequencies. We will use i1, i2, etc for multiplication factors for the tone frequency g and a1, a2, etc for amplitudes for the modulation components. Since the depth is handled by these amplitudes, we can remove β.
m[n] = a1 sin(2 π (g x i1) n) + a2 sin(2 π (g x i2) n) + ...
f[n] = g (1 + m[n] e[n]) # instantaneous frequency
θ[n] = θ[n-1] + 2 π f[n] # phase accumulation
y[n] = sin(θ[n]) E[n] # final result
The following diagram shows the processing involved.
This is the method used by Koelsynth. It is a very basic approach and can be extended further to produce much better sounds.
In an earlier attempt, I did all the music processing offline. The events used to generate large numpy arrays and I sequenced all of them based on their timing on an even larger numpy array. It worked, but the processing was not real-time. I then thought of doing the processing on a frame-by-frame basis to keep the processing real-time.
The lowest level processing block in Koelsynth is a generator - a generator of frames.
Each frame is a vector of samples (in float32).
Every generator provides a next_frame() function which returns a new frame for every call.
A generator has a fixed size once created, based on its parameters used during the creation.
Every trigger in music generation creates as a new event, which is implemented as a generator (like FmSynthGenerator). Generators are used internally and the Python interface does not support creating independent generators. All the generators are managed by the sequencer which is explained below.
Sequencer is the top-level processing block that handles the input of events and output of frames.
It keeps a list of active events. We can add new active events using its methods (eg: add_fmsynth).
We can get a frame of samples using the method next(output_np_array).
Internally it goes through all the active events, grabs one frame from each of them, adds all of them together and returns that as the next frame.
When an event is exhausted, it will be removed automatically by the sequencer.
Using Koelsynth to produce audio involves three steps:
- Creating a sequencer
- Adding events (eg:
add_fmsynth) to the sequencer - Getting audio frames from the sequencer
Add the following to your project's requirements.txt:
git+https://github.com/charstorm/koelsynth.git@main
A sequencer can be created as follows:
frame_size = 256
gain = 0.2
sequencer = koelsynth.Sequencer(frame_size, gain)Here frame_size is the number of samples per frame. The parameter gain is the amplification or attenuation that will be applied to every frame.
These control the number of harmonics used for modulation, their frequencies relative to the fundamental, and their amplitudes.
synth_params = koelsynth.FmSynthModParams(
harmonics=[2, 5, 9], # i1, i2, etc
amps=[1, 2, 1] # a1, a2, etc
)It is possible to have a multiple of these, for every instrument.
These are e[n] and E[n] explained above. Note that the values attack, decay, sustain, and release are in number of samples. They should be integer values. Koelsynth is designed in such a way that all the timing is based on samples and not in seconds, milliseconds, or microseconds.
sample_rate = 16000
sustain_duration = 2
sustain = int(sustain_duration * sample_rate)
# Modulation envelope
mod_env = koelsynth.AdsrParams(
attack=100,
decay=300,
sustain=sustain,
release=100,
slevel1=0.5,
slevel2=0.03,
)
# Waveform envelope
wav_env = koelsynth.AdsrParams(
attack=200,
decay=200,
sustain=sustain,
release=100,
slevel1=0.6,
slevel2=0.1,
)
# Make sure both have the same size
assert wav_env.get_size() == mod_env.get_size()After having these parameters, we can add events to the sequencer. This needs to be done based on some trigger (like a key-press or some algorithm).
phase_per_sample = 2.0 * np.pi * (fundamental_freq_hz / sample_rate_hz)
sequencer.add_fmsynth(synth_params, mod_env, wav_env, phase_per_sample)Here the phase_per_sample is the phase change of the fundamental signal per sample, and it decides the frequency of the sound generated.
This is the step where we get the audio from the sequencer.
frame = np.zeros(frame_size, dtype=np.float32)
sequencer.next(frame)
do_something_with(frame)Notes:
- Ideally adding events and getting frames should be done in different threads.
next(frame)will always produce a frame. If there are no events, it will be zeros. The caller must handle the timing accordingly. Otherwise, there will be a lot more samples than what the caller expected.
The following examples are currently available.
- A simple offline processing example. See
examples/simple/ - A simple real-time keyboard based piano app is provided as an example. See
examples/piano/