Testing forward and adjoint operators for Prestack Time Migration (PSTM)
The subsurface image is given by
The code main.jl shows how to use the two operators
- Demigration
$d =W L m$ where$W$ is time convolution and$L$ is the de-migration operator:
d = Operator_Conv(Operator_PSTM(m,false; Param_PSTM...), false; Param_Conv...)
- Migration
$m' = L'W' d$ where$L'$ is the migration operator and$W'$ is the adjoint of time domain convolution equivalent to time domain cross-correlation:
mig = Operator_PSTM(Operator_Conv(d,true; Param_Conv...), true; Param_PSTM...)
- In Least-squares Migration (LSM) we estimate the reflectivity by solving the following problem
operators
m_ls,J = ConjugateGradients(d,[Operator_Conv, Operator_PSTM],[Param_Conv, Param_PSTM]; Niter=20,mu=0.01)
main.jl runs an example where I use the "invere problem crime" to model data and then retrieve the model via CGLS
dot_product_test.jl checks that
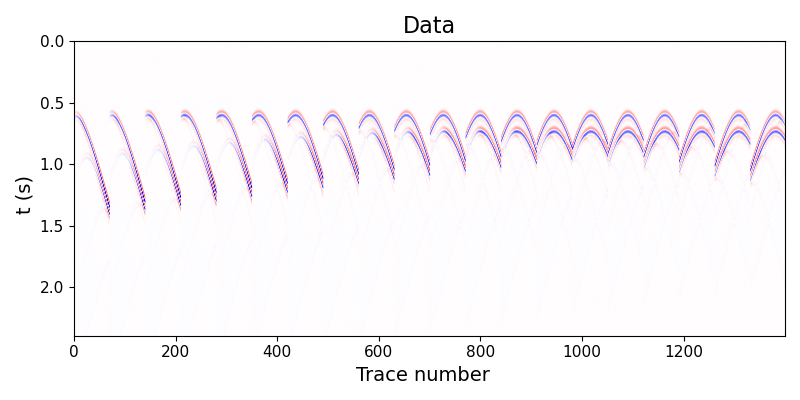
The results are shown below. First, we show the data which is computed via the demigration operator
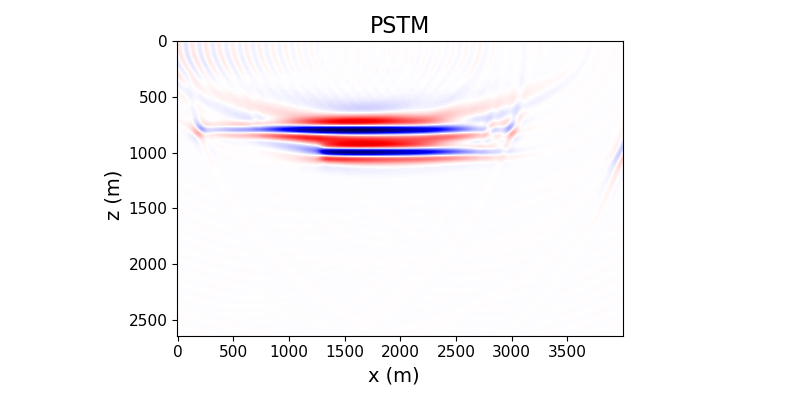
Now, I show the migrated image which is computed via
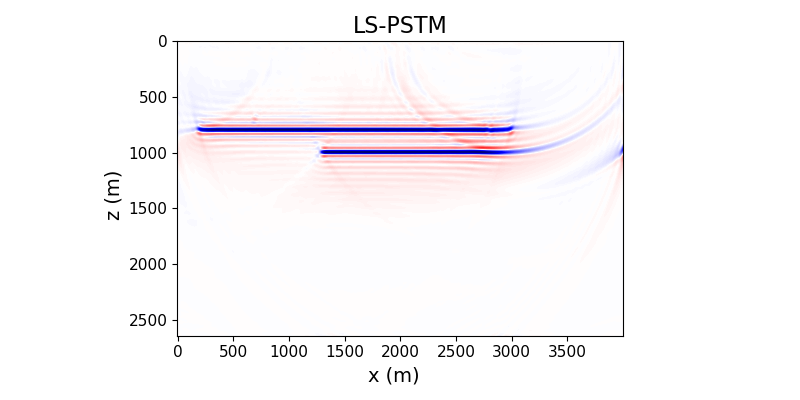
And finally, the least-squares migration after
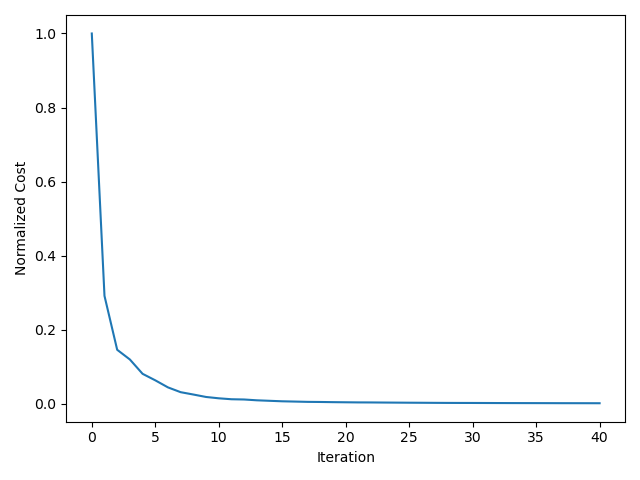
I also show the cost