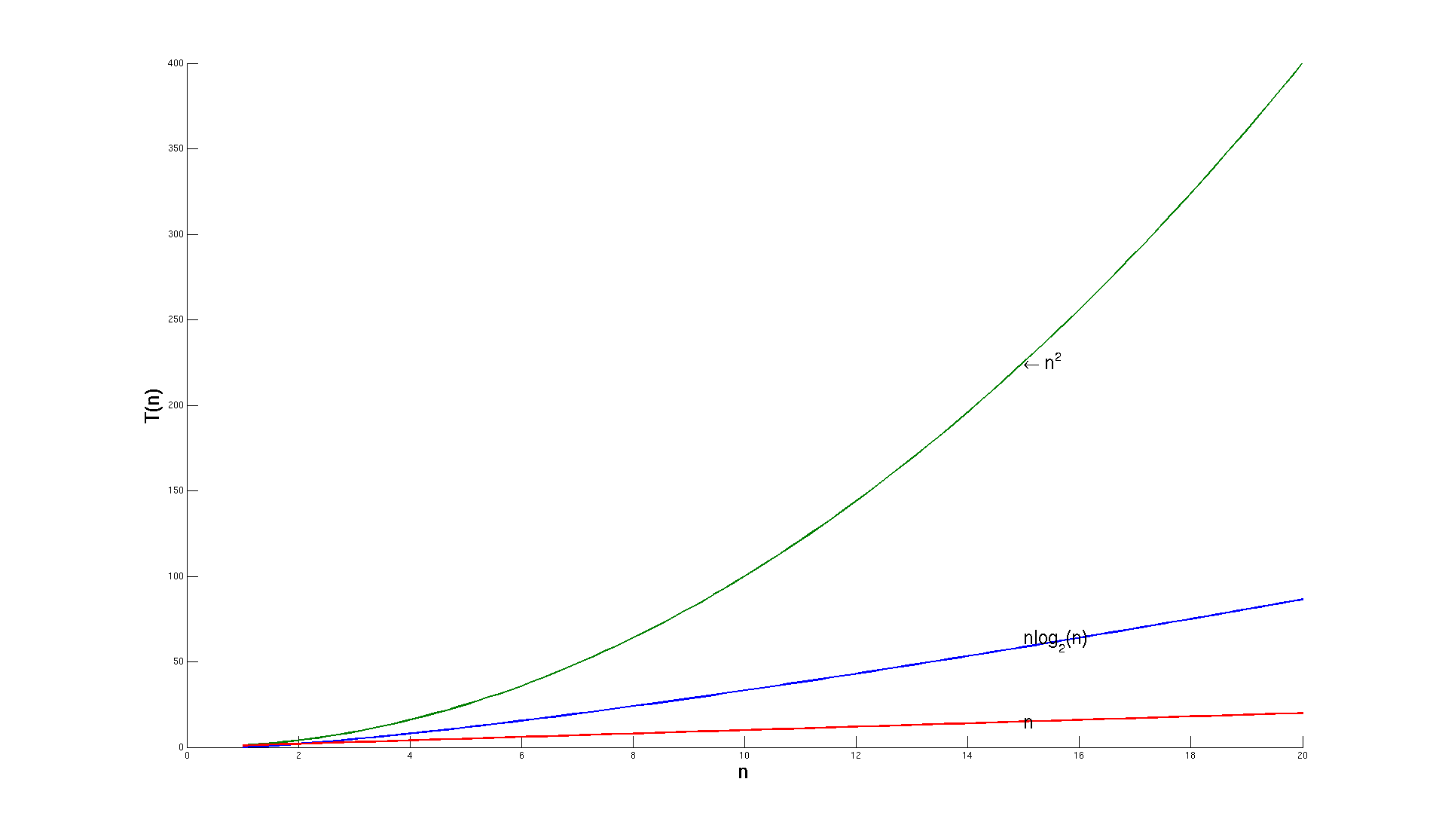
##O(n^2) vs. O(n*lg(n)) - Practical Example
It should be clear now that for any moderately large inputs, algorithms
that run in O(n*lg(n)) time will significantly outperform those that run
in O(n^2).
While one of the goals of algorithm analysis is to stay agnostic of implementation details, let's briefly take a look at what this means in practice. In this demo we'll look at a timed comparison of Merge Sort and Bubble Sort for randomized array inputs of varying sizes.
To begin, run the sorting_demo.rb script in your terminal. The demo will run 3 trials for each sorting algorithm with a randomized input of increasing size, and compute the total and average time taken to sort the arrays. As you go through this demo, note that your running times may vary significantly from mine depending on your machine and the result of the array randomizer, but should they grow at roughly the same rate.
Let's start with something small: press any key to run Merge Sort and Bubble Sort for 5 elements. The results here are fairly uninteresting: the running time for both is so small that any differences are negligible. The story is similar in running this for the next batch, 50 elements.
Now let's move on to 500 elements.
Press any key to run sorts for 500 elements:
user system total real
TTL Merge: 0.010000 0.000000 0.010000 ( 0.008129)
TTL Bubble: 0.080000 0.000000 0.080000 ( 0.080440)
AVG Merge: 0.003333 0.000000 0.003333 ( 0.002710)
AVG Bubble: 0.026667 0.000000 0.026667 ( 0.026813)
We're beginning to see some separation here between the performance of the two. In practice, though, this doesn't mean much to us; on my machine, both are still taking well under a second to run. What about 5000 elements?
Press any key to run sorts for 5000 elements:
user system total real
TTL Merge: 0.070000 0.000000 0.070000 ( 0.073389)
TTL Bubble: 8.040000 0.020000 8.060000 ( 8.082406)
AVG Merge: 0.023333 0.000000 0.023333 ( 0.024463)
AVG Bubble: 2.680000 0.006667 2.686667 ( 2.694135)
At 5000, the times start to properly diverge on my machine. Bubble Sort no longer feels instantaneous. If we were writing an application where the user needed to wait for the results of the sort to continue, this would start significantly affecting their experience.
Lastly, run the sorts for 50,000 elements. On my machine, Merge Sort still runs in a reasonable amount of time.
Press any key to run sorts for 50000 elements:
user system total real
TTL Merge: 0.830000 0.000000 0.830000 ( 0.840354)
TTL Bubble:
Can you give a rough estimate of how long Bubble Sort will take, even with randomized input? What factors would go into whether your estimate would be high or low? Picking different algorithms to solve a problem can lead to significant differences in application performance at scale.
When Bubble Sort has finished running, go ahead and play around with the input size a bit more. You can specificy the default base (as well as number of runs for averaging) by modifying SortingDemo::run_performance_tests. Approximately how long will it take to run this for 100,000 elements, based on how long your machine took to run the other tests?