/fast-matrix-nms

The Fastest Matrix NMS in the West.

Primary LanguageCudaMIT LicenseMIT

Fast Matrix NMS

A fast CUDA implementation of the matrix non-max suppression algorithm for PyTorch. Works on bounding box predictions. See SOLO v2 for the original paper, and AdelaiDet for the official implementation for masks.

This project is still in development. I am working on some more optimizations that can achieve higher throughput. Separate functions for fast IoU matrix computation and relevant stuff are also in the works.

Why

The algorithm is highly parallelizable, consisting of mainly matrix operations. When applied to mask predictions, the authors saw a huge speedup over Hard-NMS and Soft-NMS (<1ms vs 9ms vs 22ms) in their codebase. However, that excludes the time for IoU matrix computation, which is not negligible, and Hard-NMS does not necessarily require the whole IoU matrix. Also, it is unclear how efficient and optimized the implementations used for comparison are.

When applied to bounding box predictions, a naive torch implementation of matrix NMS based on the pseudo-code given in the paper, mmdetection's implementation, and AdelaiDet's implementation is much slower than torchvision.ops.nms (see benchmark). I believe that if implemented correctly, matrix NMS can be fast; that is it can at least achieve a comparable or faster speed against a pretty optimized torchvision.ops.nms.

Installation

This comes in form of a PyTorch CUDA extension. Make sure your system has CUDA installed and a CUDA-enabled PyTorch installation. To build the extension, run:

python setup.py build_ext --inplace

To install the extension, run:

python setup.py install

Usage

Once installed, it can be used similarly to torchvision.ops.nms with a little adjustment.

As of now, note that the number of boxes must be a multiple of 16, as it enables some optimization (mainly avoiding lots of warp divergence). Normally, one would first filter the box predictions over a confidence threshold and then apply NMS, now one should add more boxes or remove some boxes to satisfy the requirement, for example:

from matrix_nms import fast_matrix_nms

# boxes: (N, 4)
# scores: (N, )
boxes = boxes[:boxes.shape[0] // 16 * 16].contiguous()
scores = scores[:scores.shape[0] // 16 * 16].contiguous()

Then, apply fast matrix NMS:

# threshold: float
keep_indices = fast_matrix_nms(boxes, scores, threshold)
boxes = boxes[keep_indices]
scores = scores[keep_indices]

where threshold is the after-decay score threshold associated with the algorithm. I have not experimented a lot with this parameter. I recommend starting with 0.3-0.4 for bounding boxes and adjust accordingly. In the official repository, it seems to be 0.05 for masks.

Benchmark

The results are benchmarked using torch.benchmark on an NVIDIA RTX 2060 and AMD Ryzen 7 4800H CPUs. The benchmark script is speedtest.py.

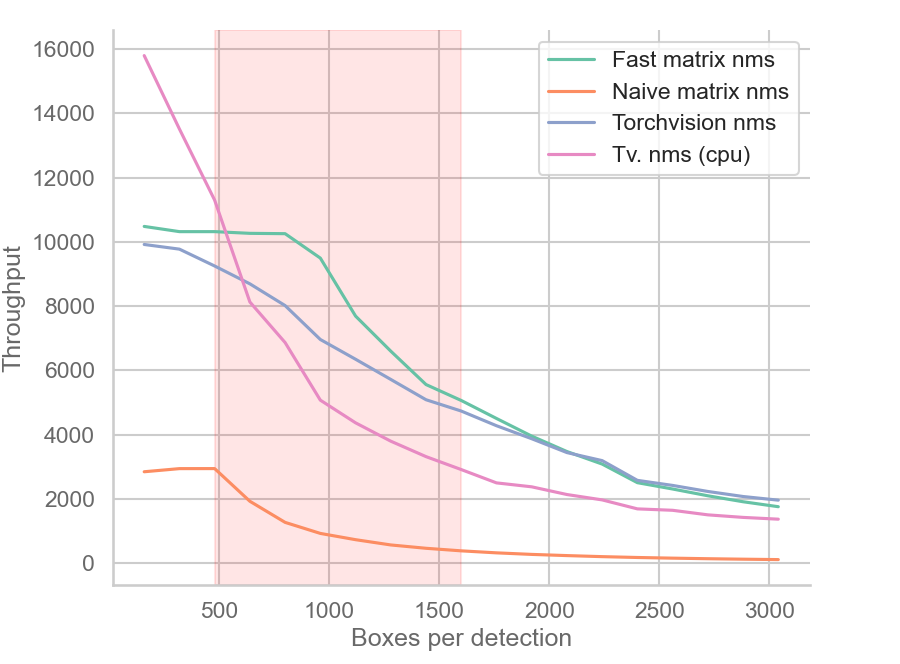
The figure way above shows the throughput (detections processed per second) of matrix NMS, torchvision.ops.nms, and a naive implementation of matrix NMS.

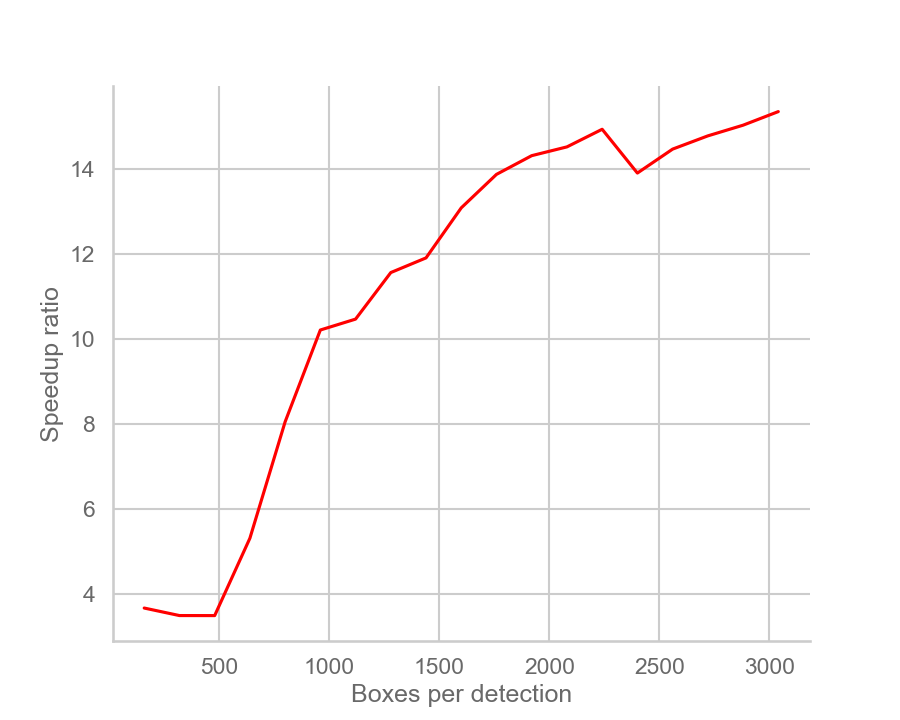
Speedup over naive implementation Inference time comparison (useless)

There are some notes to be made:

  • When the number of boxes per detection is in the 500-1500 range, fast matrix NMS has higher throughput than both CPU and CUDA versions of torchvision.ops.nms on an RTX 2060.

  • The worst and best case runtime of matrix NMS is constant and equal to the average runtime, while torchvision.ops.nms may run faster or slower depending on the input (box IoUs and threshold).

  • As the number of boxes increases over ~1600, the throughput of fast matrix NMS slowly converges to that of CUDA torchvision.ops.nms, then eventually becomes slower. This is due to my GPU hitting its parallel computation limit, plus the overhead of memory allocation and data transfer. A better GPU would see better performance and vice versa.

  • Fast matrix NMS can be further tailored for different hardware and systems, and there are more optimizations that I am working on.

How

In summary, this implementation fuses multiple steps into 3 CUDA kernels with some tricks to achieve high parallelism and low memory usage/allocation overhead:

  • Compute the lower triangular of the IoU matrix $O\in \mathcal{R}^{N\times N}$, and perform the first max reduction.
  • Perform the remaining max reduction on the IoU matrix to obtain the row-wise maximums $O_{max}\in \mathcal{R}^N$
  • Compute the possible decay factor and possible scores $S'=F(S,O,O_{max}) \in \mathcal{R}^{N\times N}$ and select the boxes to remove, skipping the finding of the minimum decay factor for each box: if $\exists i:S'_{xi}&lt;\mathrm{threshold}$, then detection $x$ should be removed.

I am writing a blog post on the details of the implementation (optimizations, tricks used, limitations, etc.) and discuss other NMS methods 😇

License

This project is released under the MIT License. Please see the LICENSE file for more information.