Binary Search in Kotlin (JVM) - Console Application

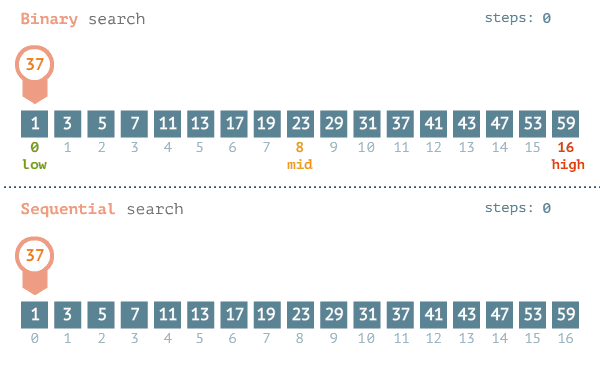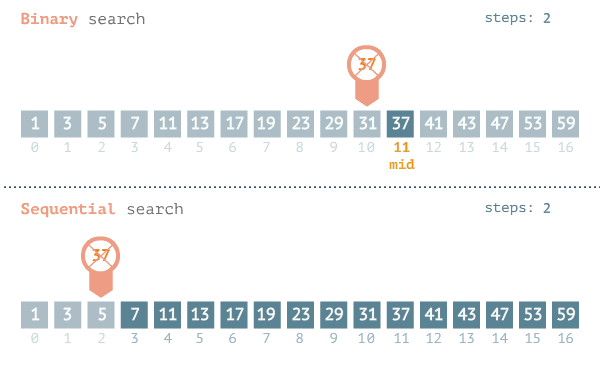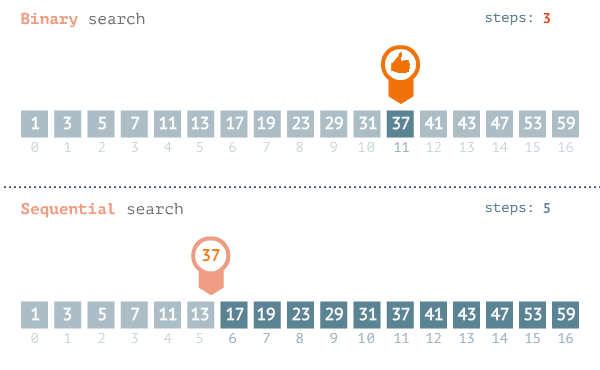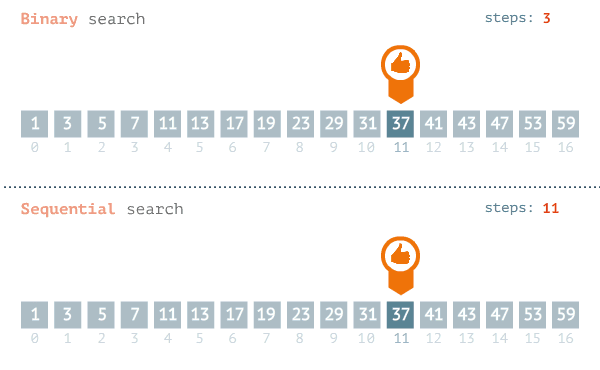
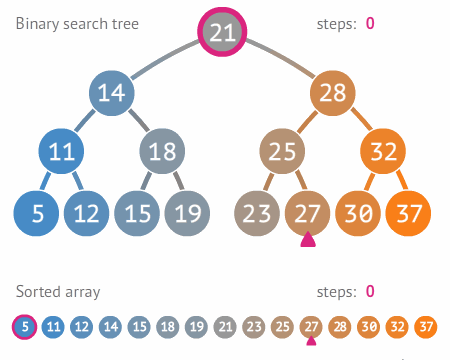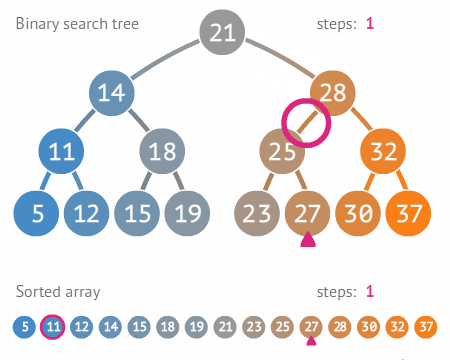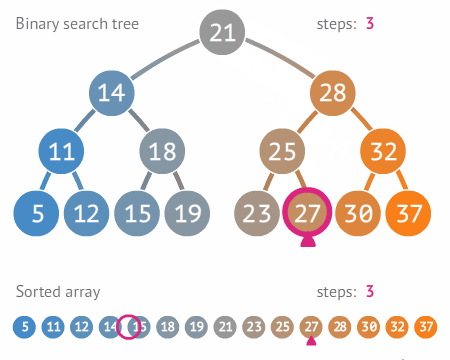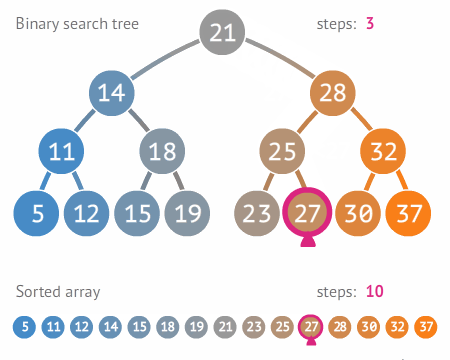
"A pesquisa ou busca binária (em inglês binary search algorithm ou binary chop) é um algoritmo de busca em vetores que segue o paradigma de divisão e conquista. Ela parte do pressuposto de que o vetor está ordenado e realiza sucessivas divisões do espaço de busca comparando o elemento buscado (chave) com o elemento no meio do vetor. Se o elemento do meio do vetor for a chave, a busca termina com sucesso. Caso contrário, se o elemento do meio vier antes do elemento buscado, então a busca continua na metade posterior do vetor. E finalmente, se o elemento do meio vier depois da chave, a busca continua na metade anterior do vetor.

-- Pesquisa Binária - Wikipedia

Dependencies

Complexity Analysis

A complexidade do algoritmo de Busca binária é da ordem de O(log n), em que n é o tamanho do vetor de busca. Apresenta-se mais eficiente que a Busca linear cuja ordem é O(n).

Procedure

Dado uma lista Α de n elementos com os valores Α₀, Α₁, Α₂, ..., Α_n-1 ordenada de tal modo que Α₀ ≤ Α₁ ≤ Α₂ ≤ ... ≤ Α_n-1, e um valor para pesquisa T, a seguinte rotina usa pesquisa binária para achar o índice de T em Α.

Defina L para 0 e R para n - 1.
Se L > R a pesquisa termina sem sucesso.
Defina m(o índice do meio da lista) para (L + R) / 2 arredondado.
Se Α_m < T, defina L para m + 1 e volte ao segundo passo.
Se Α_m > T, defina R para m - 1 e volte ao segundo passo.
Se Α_m = T, a pesquisa está feita, o índice de T é m.

Para o algoritmo computacional ser mais eficiente, foi implementado uma validação de Lista vazia, evitando-se a execução de procedimentos desnecessários!